RESEARCH ARTICLE
On the Robustness of Earthquake-Resistant Moment-Resistant Frames: Influence of Innovative Beam-to-Column Joints
Antonella Bianca Francavilla1, *, Massimo Latour1, Gianvittorio Rizzano1, Jean-Pierre Jaspart2, Jean-Francois Demonceau2
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
Issue: Suppl-1, M4
First Page: 101
Last Page: 111
Publisher ID: TOBCTJ-12-101
DOI: 10.2174/1874836801812010101
Article History:
Received Date: 1/10/2017Revision Received Date: 1/11/2017
Acceptance Date: 1/12/2017
Electronic publication date: 23/3/2018
Collection year: 2018

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
The deformation capacity of beam-to-column connections strongly influences the robustness of earthquake-resistant Moment Resistant Frames (MRFs) when subjected to a loss-of column scenario. As a consequence, with the aim of foresee the structural response up to the failure, an accurate modelling of the ultimate behaviour of the joints is needed.
Objective:
In this paper, the influence of the connections on the behaviour of MRFs under a loss-of-column scenario has been analysed considering an accurate modelling of the joints.
Method:
In addition, in order to achieve this goal, different beam-to-column joints designed for seismic actions and tested at the Salerno University, have been modelled and introduced in a case-study structure, whose response has been evaluated by means of push-down analyses. In particular, the connections analysed and modelled are of three different types: a dog-bone connection, a partial strength Double Split Tee (DST) joint and a partial strength connection with friction dampers.
Results / Conclusion:
The results of pushdown analyses performed by means of SAP2000 computer software have been examined with the aim to determine the Residual Reserve Strength Ratio (RRSR) index that, combined with the energy balance method proposed by Izzudin et al. (2008), allow to assess the structural ro-bustness.
1. INTRODUCTION
The recent terroristic attacks that occurred in Europe and USA have underlined the importance to assess the robustness of structures designed according to the current seismic and non-seismic codes. It is well known that the resisting capacity to the progressive collapse is strictly linked to the local and global ductility supply and, consequently, to the monotonic energy dissipation capacity of the elements undergoing plastic deformation. Generally, steel Moment Resisting Frames (MRFs) in seismic zone, due to the detailing rules followed in the design process, are normally ductile and thus good candidates to resist to the progressive collapse caused by the local failure of the major loading resisting elements. However, during severe earthquakes such as Northridge and Kobe, the brittle failures occurred in the beam-to-column joints have underlined the role assumed by joints both when they are designed as Full Strength (FS) and when they are designed as Partial Strength (PS). In fact, if not properly assessed in the design phase, sometimes the limited local ductility of some joint components can jeopardize the overall behaviour of the structure. Therefore, in order to accurately predict the structural performance, a proper modelling of beam-to-column joints is necessary. The current methodology for the prediction of behaviour of joints suggested by Eurocode 3 [1] is based on the so-called component method [2, 3], which provides to break-up joints in single components that are first characterized in terms of stiffness and resistance and then assembled in a mechanical model able to provide the response of the whole connection. Nevertheless, even though the component method is already very advanced, there are still some limitations related to the prediction of the ductility of each joint component and to the possibility to account for axial forces activating after the development of catenary effects. These two aspects are analysed and modelled in the following.
Regarding the evaluation of the structural robustness, several approaches can be followed: risk based robustness index, energy based partial pushdown analysis and deterministic robustness indexes [4-6]. In this paper, the performance of the analysed frames is evaluated and compared using the Residual Reserve Strength Ratio (RRSR) index [5], i.e. a quantitative index to assess the robustness of damaged structures, and to quantify the progressive collapse resistance of real complex structures. This approach has been combined with the energy balance method [6] that adopts a simplified approach evaluating the maximum dynamic response from non-linear static response. In this framework, pushdown analyses of the structures by varying the beam-to-column connections have been performed in SAP 2000 computer program. To this scope, preliminarily the component method for predicting the whole moment-rotation curve of the joint has been applied proposing some modifies in order to account for the development of membrane forces in the connection and to introduce the ultimate deformation of the single joint components. In particular, a refined model for the prediction of the elastic and ultimate behaviour, in terms of stiffness, resistance and ductility of the T-stub has been developed [7]. In addition, this approach has been extended to the other joint components that could be modelled by means of an equivalent T-stub.
2. INVESTIGATED BEAM-TO-COLUMN CONNECTIONS
Although the traditional design practice suggests the use of rigid full strength joints, Eurocode 8 [8] has already opened the door to the possibility to dissipate the seismic energy in the connecting elements of the beam-to-column joints. In this case, semi-rigid partial strength connections have to be designed by means of an appropriate choice of the components where the energy dissipation has to occur. Aiming to investigate the performances of different joint typologies under seismic loading conditions and the accuracy of the approach followed to design the joints an experimental campaign regarding different typologies of bolted beam-to-column connections has been performed in the past at the STRENGTH laboratory of Salerno University [9-10]. In this paper, starting from the above-analysed joints typologies, the attention is focused on their performances when adopted in Steel Moment Resisting frames subjected to a loss of a column scenario.
2.1. Typologies of Beam-to-Column Joints
The joint typologies considered in the development of the Robustness analyses are characterized by similar resistance and initial stiffness even though they are very different in terms of joint details. In particular, the following joint typologies are considered:
- EEP-DB-CYC03: a full strength extended endplate joint designed to force the development of the plastic hinge in the beam by cutting the beam flanges (Fig. 1a) according to the design criteria for reduced beam sections (RBS).
- TS-CYC04: a partial strength joint with a couple of T-stubs bolted to the beam flanges and to the column flanges and designed to be the main source of plastic deformation capacity (Fig. 1b).
- FREEDAM-CYC01: a partial strength joint equipped with friction device realized by means of a haunch composed by horizontal steel plates with normal holes except the inner plate realized in 1.4301 Stainless Steel and bolted to the pre-stressed friction shims with M20 class 10.9 HV bolts and 6 disc springs (Fig. 1c).
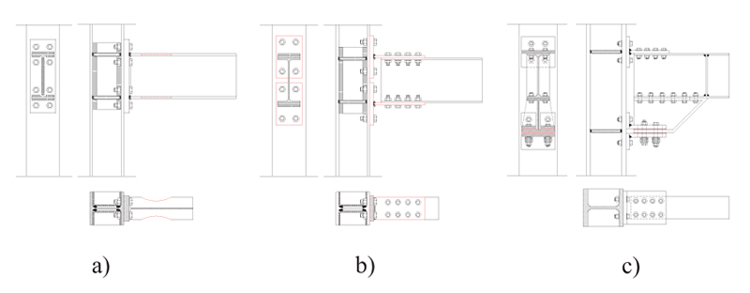 |
Fig. (1). Typologies of joints: a) EEP-DB-CYC03; b) TS-CYC04; c) FREEDAM-CYC01. |
The main geometrical parameters of the connecting elements of the beam-to-column joints are reported in Table 1 with reference to the notation of (Fig. 2).
| Joint | Bolts | Pre-loading | bep | hep | tep | e1 | e2 | p1 | p2 | p3 |
|---|---|---|---|---|---|---|---|---|---|---|
| EEP-DB-CYC 03 | 8 M24 (10.9) | 550 Nm | 427.0 | 161.0 | 25.3 | 36.0 | 33.0 | 89.0 | 99.0 | 163.0 |
| TS-CYC 04 | 8 M20 (10.9) | 550 Nm | 154 | 2x257 | 25.2 | 30.2 | 39.0 | 94.3 | 177 | - |
| FREEDAM-CYC 01 | 8 M30 (10.9) | 550 Nm | 162.0 | 2x253 | 25 | 41.0 | 40.0 | 81.0 | 173 | - |
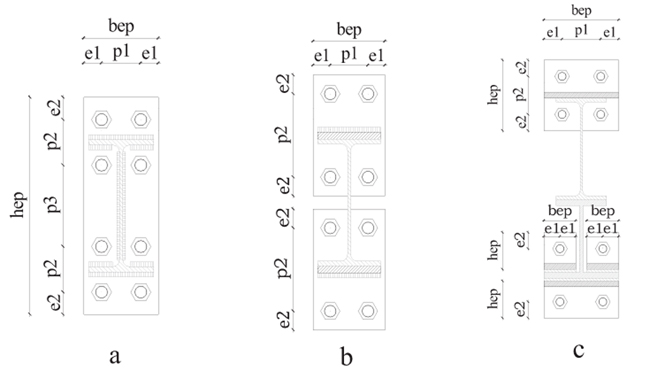 |
Fig. (2). Notation for the geometrical properties: a) EEP-DB-CYC03; b) TS-CYC014; c) FREEDAM-CYC01. |
In addition, the mechanical properties of the dissipative elements of the joints represented by the endplate for EEP-DB-CYC 03 and by the flange of the tee elements for the TS-CYC 04 are given in Table 2 .
| Joint | fy [N/mm2] | fu [N/mm2] | E [N/mm2] | εh/εy | εu/εy | E/Eh | E/Eu |
|---|---|---|---|---|---|---|---|
| EEP-DB-CYC 03 | 290 | 493.7 | 207288 | 11.3 | 589 | 86.5 | 632.8 |
| TS-CYC 04 | 295 | 520.0 | 210000 | 12.2 | 486 | 103.4 | 486.0 |
In Table 3 , the mechanical properties of the column and beam are summarized. In all the joints configuration, the column size is HE 200 B while the beam size is IPE 270.
| All Joint | fy,f [N/mm2] | fu,f [N/mm2] | fy,w [N/mm2] | fu,w [N/mm2] |
|---|---|---|---|---|
| Column | 430 | 523 | 382.5 | 522 |
| Beam | 405 | 546 | 387 | 534 |
2.2 Extension of the Component Approach to Joint Subjected to Axial and Bending Loads
Within the framework of the component approach, the flexural capacity of the whole joint can be calculated starting from the resistance of the single joint components. Preliminarily, it should be emphasized that the connection, panel zone and beam can be seen as three macro-components in series, where connection and panel zone constitute the so-called joint, while beam and joint compose the so-called beam-joint system (Fig. 3). Under this last point of view, beam and joint can be regarded as two macro-elements in series whose contribution to the plastic deformation capacity is given by an accurate balance of the thresholds of the first plasticization and ultimate strength [2]. Hereinafter, the main principles followed in the modelling of the macro-components needed to set-up the model of the frame are reported. The main macro-components are the beam end, the joint and the column.
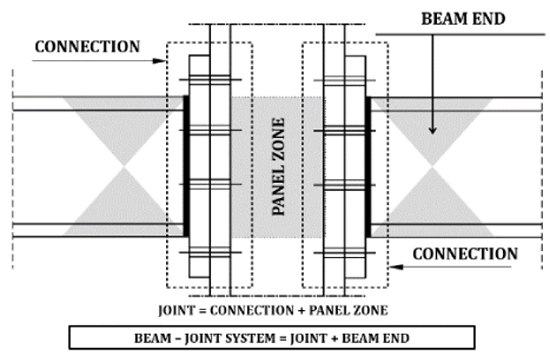 |
Fig. (3). Beam-joint system. |
The plastic deformation capacity of the beam has been taken into account performing preliminary analyses by means of ABAQUS software calibrating the behaviour of a M-N-θ zero-length spring to be included in the beam-joint system idealisation.
To this scope, several FE simulations have been preliminarily running in order to derive the moment-rotation curve of the beam shapes considered in the push-down analyses reported afterwards when subjected to a combined tensile force (such as those activated during a push-down analysis) and bending moments. In particular, the analyses have been performed for five fixed values of the nondimensional tensile axial force, ρ=Nt/Npl with Nt equal to the tensile axial force and Npl the full plastic axial load, increasing progressively the value of the imposed rotation (Fig. 4).
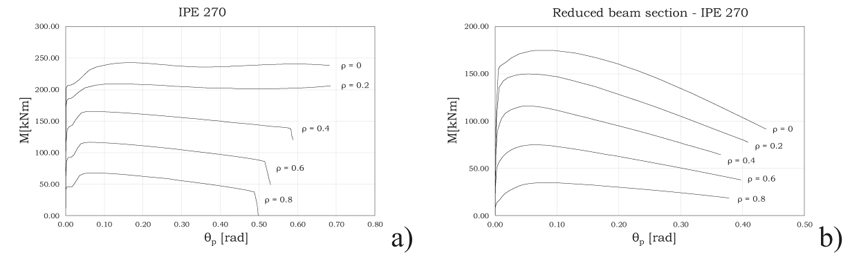 |
Fig. (4). Moment - rotation curves: a) IPE 270 profile; b) reduced beam section. |
With reference to the prediction of the response of the connections, it should be highlighted that, in case of bolted extended endplate connections having three or more bolt rows in tension, a refined model (Fig. 5a) has to be adopted in order to take into account the interaction between the different bolt rows. Nevertheless, with the aim of simplifying the modelling of the connections, the prediction of the response of the connections is carried out by means of the simplified mechanical model proposed by the Eurocode 3 [1] and depicted in Fig. (5b) with only one spring in the tension side.
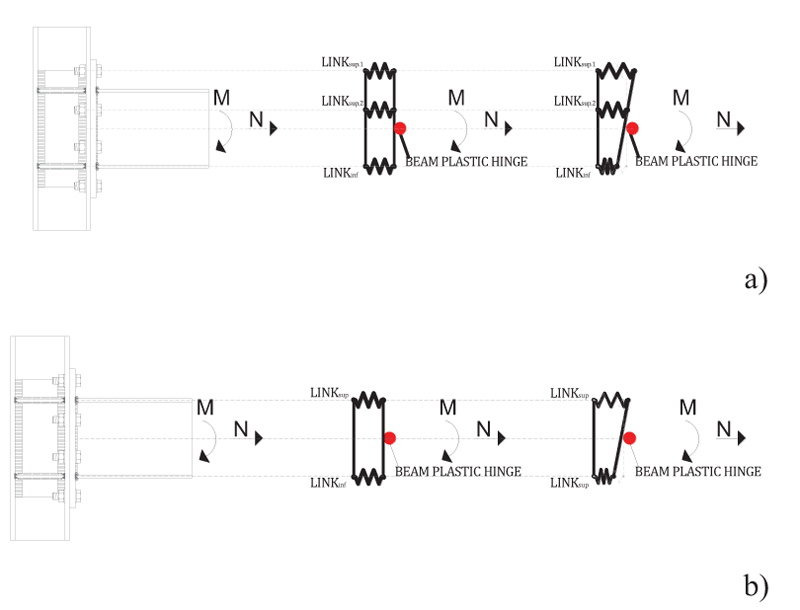 |
Fig. (5). Mechanical model for the bolted connections: a) refined model; b) simplified model. |
Generally, in case of column loss, the joints are subjected to combined bending moments and axial forces; nevertheless, also in these cases, the component method is still valid provided that each joint component is adequately modelled up to the ultimate condition in tension or compression. In particular, in order to take into account for both bending and axial actions, each component has been characterized by an extensional spring represented by a F-δ curve, where F is the force action in the component and δ is the related displacement.
With reference to the all considered joints typologies, the following components have been modelled in terms of stiffness, resistance and ductility: column web in shear, column web in compression, column web in tension, beam flange and web in compression, beam web in tension, column flange in bending, bolt in tension, endplate in bending, beam flange in tension. In addition, for the bolted tee-stub connections other components have been considered: T-stub web in compression, t-stub web in bearing, beam flange in bearing, bolts in shear; t-stub web in tension. Regarding the joint components modelled by means of an equivalent T-stub, i.e. the column flange in bending, endplate in bending and tee elements in bending, in this paper the theoretical model developed in [7] has been adopted. This model allows to the definition of the T-stub response up to failure, starting from the definition of the geometry of the elements, the boundary conditions and the non-linear behaviour of its subcomponents, i.e., the plate and the bolts. Finally, starting from the force-displacement curve of each joint component, the mechanical models of the whole joints have been obtained for the robustness analyses of steel frames. Differently, the deformation capacity of the column has been taken into account by means of a plastic hinge characterized by a rigid-plastic behaviour with hardening constitutive law as depicted in Fig. (6).
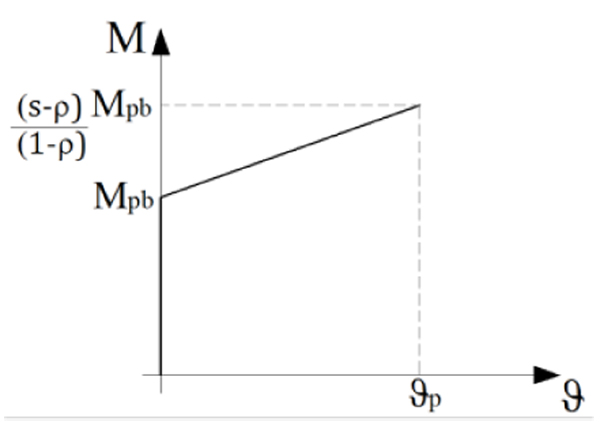 |
Fig. (6). Moment - rotation curve. |
where Mpb is the plastic bending moment, sMpb is the bending moment corresponding to the occurrence of local buckling of the beam compressed flange and ϑp is the ultimate rotation provided by the beam end. The parameter s is the non-dimensional buckling stress depending on the width-to-thickness ratios of the plates elements constituting the beam section and on the longitudinal stress gradient. Starting from analysis of the experimental data, by means of a multiple regression analysis, Mazzolani and Piluso [11] defined the following empirical relationship:
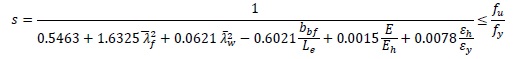 |
(1) |
where λf and λw are, respectively, the normalized slenderness parameters of the flange and of the web equal to:
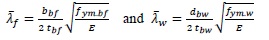 |
(2) |
bf is the flange width, tf is the flange thickness,dw is the compressed part of the beam web, tw is the web thickness, Le is the shear length of the beam, E is the Young modulus, Eh is the hardening modulus, εy is the strain corresponding to yielding and εh is the strain corresponding to the end of the yield plateau. The ultimate curvature is given by [11]:
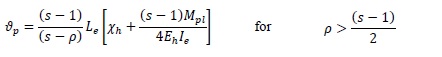 |
(3) |
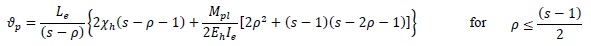 |
(4) |
where χh is the curvature at the end of the yield plateau, Ie is the moment of inertia of the two-flange section.
3. ROBUSTNESS ANALYSES
Generally, the robustness analysis of structures subjected to a loss-of-column scenario is performed removing one or several primary elements and then analysing the capability of the structure to absorb the damage. Different methods for analysing the progressive collapse are available: linear-elastic static, nonlinear static, linear-elastic dynamic and nonlinear dynamic procedures. In the former method, the structure is analysed in elastic range under amplified combination of loads and the structural response is evaluate in terms of ratios between demands and capacities; however, this kind of analysis is limited to the structures whose dynamic and nonlinear behaviour is easily predicted. Although the linear dynamic analyses and even more the nonlinear ones are very accurate, they are usually avoided due to their complexity and because the evaluation and the comparison of the results are very time-consuming. Therefore, the nonlinear static analyses represent the most suitable approach for robustness analyses because they are able to take into account the nonlinear effects and to determine the elastic and failure limits of the structure. The capacity of the damaged structure is evaluated in terms of overload factor λ corresponding to the occurrence of the first failure in the structure. This approach, often called pushdown analysis, will be followed in this paper in order to assess the robustness of the study case frames.
According to the seismic design, in MRFs the energy dissipation is concentrated in some zones of members that are engaged in plastic range so that they have been properly detailed. The structural typologies herein investigated are MRFs designed according to the theory of plastic mechanism control that assures a collapse mechanism of global type in case of seismic actions. In particular, this design procedure is based on rigid-plastic analysis and on the kinematic theorem of plastic collapse extended to the concept of mechanism equilibrium curve [12]. In order to evaluate the global robustness, four bays - six storeys frame have been considered whose interstorey heights are equal to 3.20m except for the first storey whose height is equal to 3.50m while the bay span is equal to 6.00m (Fig. 7).
Regarding the design loads, a uniform dead load Gk = 12.00 kN/m and a uniform live load Qk = 6 kN/m have been considered. Considering the applied vertical loads according to the combinations provided by Eurocode 8 [8], IPE270 made of S275 steel grade have been adopted while the size of the columns, made of S275 steel grade, have been designed according to the procedure suggested by Piluso et al. [12-14] able to guarantee a collapse mechanism of global type. In order to perform pushdown analyses, the design vertical load distribution has been determined in accordance with the accidental load combination, i.e. q = Gk + Qk = 18.00 kN/m. The structure has been modelled and analysed in SAP 2000 analysis software. The model is conceived to account for both material and geometrical nonlinearities.
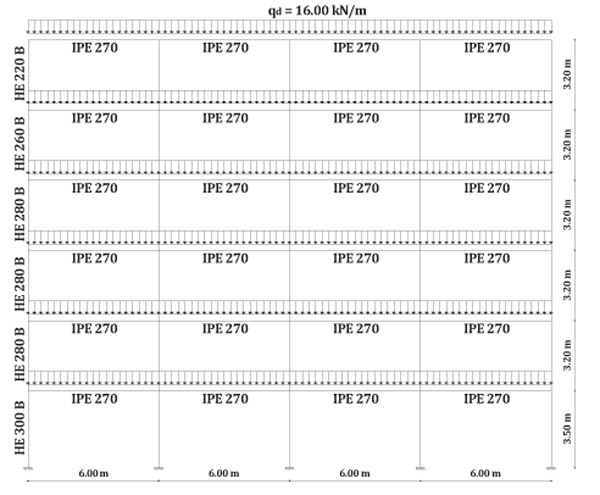 |
Fig. (7). Analysed structural scheme: initial conditions. |
With reference to the members, they have been modelled by means of elastic frames adopting a lumped plasticity approach: both for beams and columns plastic hinges accounting for the M-N interaction, defined according to European code, have been considered. Beam-to-column connections have been modelled by means of link elements connected by rigid frames accounting for the stiffening effect of the beam web and the distance between the tension flange level and the centre of compression, i.e. the laver arm z (Fig. 8). The latter parameter has been considered, using the simplified method proposed by the Eurocode 3 [1], as the distance from the centre of compression to the point midway between the two bolt-rows in tension. Indeed, in the analysed connections, this assumption is acceptable because the bolt-rows in tension are close enough and symmetric with respect to the beam flange.
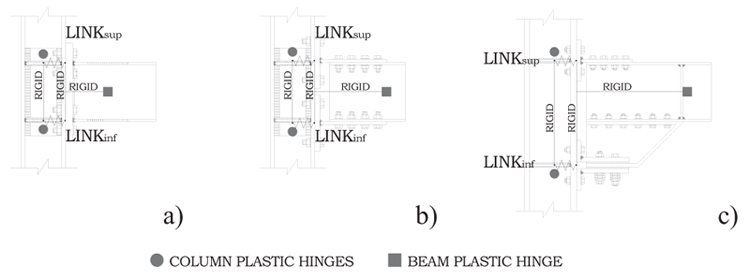 |
Fig. (8). Bolted joint’ structural scheme: a) dogbone connection; b) tee-stub connection; c) friction connection. |
3.1. Results of the Pushdown Analyses
For the pushdown analyses, the internal force distribution in the element to be removed, i.e. the column in the middle at the first storey, has been initially determined and the column segment has been replaced by the equivalent axial reaction (Fig. 9).
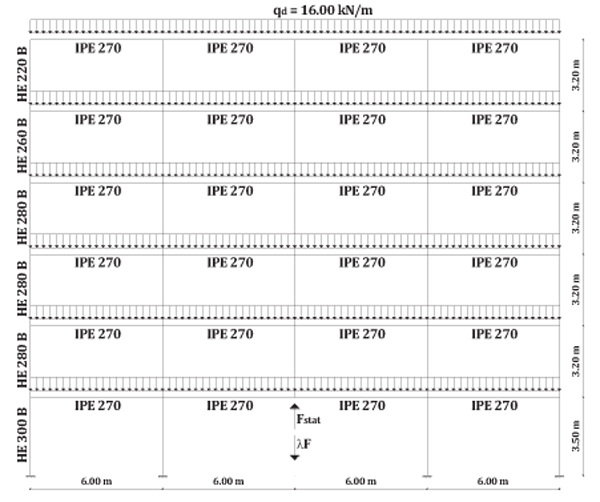 |
Fig. (9). Analysed structural scheme: pushdown configuration. |
Subsequently, the pushdown curve has been obtained by increasing vertical displacements of the node to which equivalent column reaction force has been applied. In detail, a force
The typical curve representing the evolution of the vertical displacements according to the progressively remove of the column, is reported in Fig. (10a). In particular, 3 phases can be recognized [15,16]: the first phase corresponds the elastic behaviour; the second phase begins when the first plastic hinge develops; the third phase starts when actions in the collapsed column reach the zero value. In the last phase high deformations and second order effect become very important factors to be taken into account and catenary effects develop in the beams of the directly affected part. With the aim to compare the structural performance of the MRFs analysed by varying the bean-to-column detail, the Residual Resistance Strength Ratio has been determined. This parameter has been evaluated starting from the energy balance method proposed by Izzudin et al. [6].
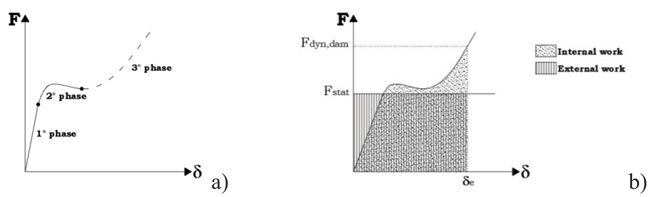 |
Fig. (10). Nonlinear structural response. |
Following this approach, the energy conservation has been used in order to estimate the maximum dynamic response starting from the static response obtained by means of nonlinear analyses as the pushdown ones. In particular, in order to take into account the inertial and nonlinear effects, a Dynamic Load Factor (DLF) can be expressed as:
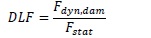 |
(5) |
where Fdyn,dym is the equivalent amplified force for which the system reaches equilibrium in the damage state and Fstat is the value of the static gravity loads on the resisting element before to notional removal. The value of Fdyn,dym is evaluated imposing the equilibrium in the damaged state. In particular, equating the internal work and the external one, the value of the displacement in dynamic equilibrium condition and the corresponding force Fdyn,dym has been determined (Fig. 10b). The internal work is given by:
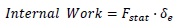 |
(6) |
while the external work is computed as:
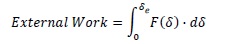 |
(7) |
where δe the equivalent dynamic displacement at equilibrium. When the internal work is equal to the external one, the equilibrium in the damage state is achieved. Determined the dynamic load factor, the Residual Reserve Strength Ratio (RRSR) of the structure has been calculated as:
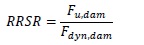 |
(8) |
where Fu,dam is the ultimate capacity of the structural system in the damaged configuration that has been evaluated in correspondence of the achievement of the ultimate resistance of the weakest component, whether it is a nodal component or the end of the beam. With reference to the directly affected part of the structures (Fig. 11), the force-displacement curves of the most stressed beam-to-column joints have reported for each performed analysis. In particular, the monitored joint “A” is subjected to the hogging moment whose value increases when the column fails while the joint “B” is subjected to hogging moment when the vertical distributed load are applied and to sagging moment in the loss-of-column scenario.
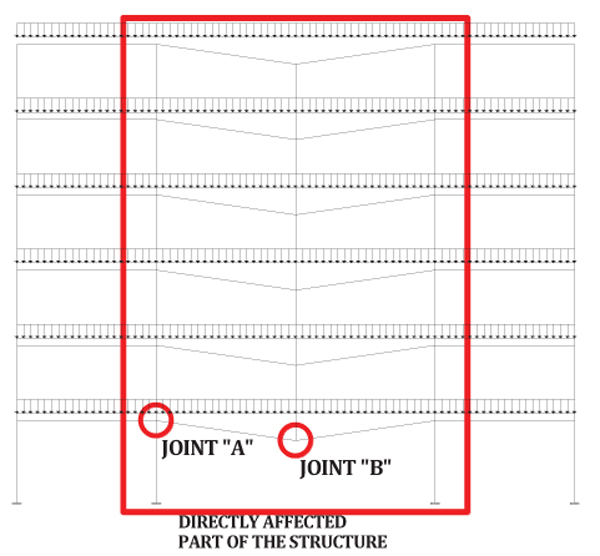 |
Fig. (11). Analysed beam-to-column connections of the directly affected structure. |
The results obtained by means of the analyses in terms of F-δ curve are reported (Fig. 12) therefore the increasing value of force λFstat has been plotted on the vertical axis while the corresponding displacement on the horizontal axis; the circular markers on the curves represent the static force while the square markets represent the equivalent dynamically amplified force.
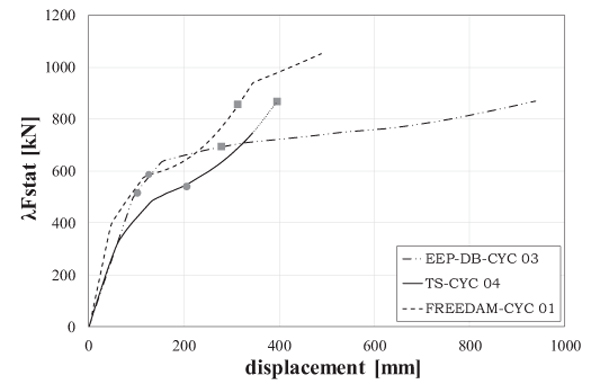 |
Fig. (12). Pushdown curves. |
It can be observed that in case of TS-CYC 04 connection typology, the energy balance is not obtained, therefore the zero kinetic energy condition is not reached and global structural collapse occurs. It means that is not possible, in those cases, to determine the value of the dynamically amplified force and, as a consequence, the residual reserve strength ratio. Conversely, in case of EEP-DB-CYC 03 and FREEDAM-CYC 01 the energy balance is obtained and the structures exhibit a residual strength reserve. In Table 4, the main results of the pushdown analyses have been reported. The values of the dynamic load factor are in between 1.35 and 1.61 while the residual reserve strength ratio value is equal to 1.18 in case of EEP-DB-CYC 03 connection and equal to 1.23 in case of FREEDAM-CYC 01 connection.
| JOINT | Fstat [kN] | DLF | RRSR | Failure modes |
|---|---|---|---|---|
| EEP-DB-CYC 03 | 512.4 | 1.35 | 1.18 | Connecting beam |
| TS-CYC 04 | 538.56 | 1.61 | 0.86 | Upper T-stub |
| FREEDAM-CYC 01 | 585.11 | 1.46 | 1.23 | Upper T-stub |
In Table 4, an additional information is related to the failure modes of the connection that determine the global collapse. In all the cases, in line to what is expected, the structural collapse is related to behaviour of the joint component designed as the weakest.
CONCLUSION
The global behaviour of MRFs equipped with traditional and innovative beam-to-column joints under a loss-of-column scenario has been investigated. The results of pushdown analyses performed by means of SAP2000 computer software have been examined with the aim to determine the Residual Reserve Strength Ratio (RRSR) that allows to assess the structural robustness. The comparison among the structures analysed by varying the beam-to-column detail shows that, even though Steel Moment Resisting Frames equipped with both traditional and innovative connections result in exhibiting a residual strength reserve, the employment of the FREEDAM connections guarantees significant benefits. In fact, the required plastic deformation capacity at the level of the joints is much smaller when using the FREEDAM joints. It is mainly due to the fact that the slip of some joint components during the column loss provides flexibility to the system and so allows activating an alternative load path for the load redistribution before reaching the plastic resistances in the system.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The research related to the study of the friction connections has received funding from the European Union's Research Fund for Coal and Steel (RFCS) research programme under grant agreement n° RFSR-CT-2015-00022 FREE from DAMage Steel Connections (FREEDAM).








