RESEARCH ARTICLE
Preliminary Study on Beam-To-Column Joints Under Impact Loading
Marina D’Antimo1, *, Massimo Latour2, Gianvittorio Rizzano2, Jean-François Demonceau1, Jean-Pierre Jaspart1
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
Issue: Suppl-1, M5
First Page: 112
Last Page: 123
Publisher ID: TOBCTJ-12-112
DOI: 10.2174/1874836801812010112
Article History:
Received Date: 1/10/2017Revision Received Date: 1/11/2017
Acceptance Date: 1/12/2017
Electronic publication date: 23/05/2018
Collection year: 2018

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
Recent catastrophic events have pointed out the need to ensure the integrity of structures under “exceptional” events. Since many years, the University of Liège is involved in different activities and projects related to the robustness assessment of structures. The robustness of a structure is the ability of the system to remain globally stable after events not directly accounted for in the design, like impact, fire or consequences of a human error, which should lead to a reasonable damage when compared to the original cause.
Objective:
The presented preliminary work reports the experimental campaign of different European projects (FREEDAM and ROBUSTIMPACT) carried out or currently ongoing, with the aim of understanding the behaviour of different joint typologies under impact loading protocol.
Method:
The experimental programmes have mainly regarded static and impact tests on steel joints by the means of a dropping mass using DIC (Digital Image Correlation) for the data acquisition.
Conclusions:
In the present paper, an overview on the design criteria adopted in the design of the experimental campaign, for the FREEDAM project, is given, and some earliest results are discussed.
1. INTRODUCTION
The consequences of an impact on a structure involve a large set of variables such as large displacements, material non-linearity, instability, etc. All these aspects lead to the definition of a complex physical problem difficult to describe with a simple approach. Currently, dealing with this topic, the scientific literature is rather limited but owing to an increased interest, many researches have focused on the case of extreme loading conditions [1-3]. The research unit at Liege University has devoted several works and research to the robustness of buildings under exceptional events [4-11], with a special focus on a particular loading case: the column loss scenario [3-4] which may occur due to an impact or an explosion. Knowing how the loads are redistributed within the structure by activating alternative load paths, it is possible to check if its integrity can be ensured and so, if the progressive collapse within the structure can be avoided. Focusing the attention on the behaviour of joints under impulsive loading, the high strain-rate can significantly influence the behaviour of the joint components, and the absorbed energy when compared to the static behaviour. Two European projects are strongly linked to this topic: the RFCS project called “ROBUSTIMPACT” [12], where an experimental campaign on steel and composite joints under impact loading [13] has been performed and some design rules have been derived; and a part of the ongoing FREEDAM project which is devoted to the behaviour of a particular joint typology, equipped with friction dampers, under impulsive loadings. The purpose of this experimental campaign is to evaluate the influence of high strain rates on the components of the particular connection proposed in the project, in order to ensure a robust behaviour of the joint. The present paper reports a brief overview on the experimental programme of FREEDAM, which is still ongoing. Additionally, a critical discussion of the first experimental results is reported.
2. JOINTS UNDER IMPACT
Several scenarios can lead to a situation in which the joint is subjected to an exceptional loading condition. For example, the column damage scenario, due to impact or blast, is considered as a benchmark case [3, 4, 8, 14] in which due to the loss of a column, a load situation not accounted for in the design phase can occur. Under the occurrence of such unpredicted scenario, the optimum behaviour would be characterized by the activation of an alternative load path, able to avoid the progressive collapse of the structure. In order to obtain this behaviour, the structure needs to remain globally stable and the joints have to be able to dissipate the required level of energy. In principle, a satisfactory static behaviour of the joint does not ensure an appropriate behaviour under impulsive or exceptional loading conditions, hence, there is usually the need for further investigations accounting for the effect of strain rates. The component method is a widely used procedure to predict the behaviour of joints, which are considered as an assembly of basic components; each component is modelled as a spring and characterized by a resistance and a stiffness. The methodology is derived for the static characterization of the connection and its extension to joints under exceptional loading is not straightforward. To overcome this knowledge gap, several researches have been undertaken in order to assess the influence of the strain rate on the joint response [15-18]. For bolted end-plate connections at the moment the technical literature is not in common agreement. In [19] the authors found an increase of the dissipation capacity and ductility of the studied connections when compared to the static test. Conversely in [16], a decrease of ductility and an increase of stiffness was recognized in flexible end plate connections. The proposed connection is expected to have a higher ductility compared to traditional joint solutions; it is designed to behave in a ductile way activating plastic deformations in one or more joint components, and to perform in a suitable way when large displacements are required (i.e. under column loss scenario).
2.1. Design Criteria for FREEDAM Joint
The FREEDAM connection Fig. (1a) can be considered a modification of a DST (Double Split Tee) joint where the bottom tee is replaced with a friction damper constituted by a couple of angles and pre-loaded friction pads, Fig. (1c) located on an additional haunch bolted to the lower flange of the IPE220 beam by means of M12 class 10.9HV bolts. The beam upper flange is connected through a bolted T-stub to the column (HE 200B) while the lower flange is bolted to an additional haunch connected to the column by a system of angles. A steel plate coated with a proper friction material is located between the haunch flange and the angles, constituting the friction damper. Furthermore, in order to have an adequate stroke for the friction damper, the haunch flange has several slotted holes. All the elements are made of S275JR steel except for the haunch flange, which is made of stainless steel AISI 304, all the details are given in Fig. (1). With this geometry, under bending actions, the connection rotates allowing easily large displacements. The energy dissipation is provided by the slippage of the haunch flange on the friction pads, ensuring that under frequent and destructive seismic events the damage is limited. The design of the proposed connection is a key issue of the project and due to the specific seismic purposes, the application of capacity design rules is required. In a first step, the dissipative component, the friction damper, is designed according to the first principle of the capacity design, namely in order to carry the seismic design actions. The extended procedure is given in [20].
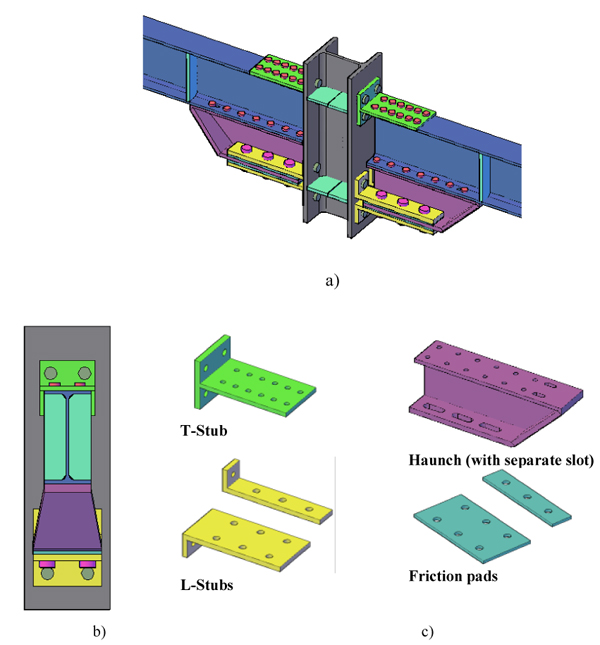 |
Fig. (1). a)Proposed connection; b) Lateral view; c) Joint details. |
Therefore, by proper application of hierarchy criteria, the friction damper is designed to be activated before the other components are engaged in plastic range; the slip force of the damper is given by:
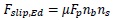 |
(1) |
where Fp is the chosen level of preload in the bolts; μ is the friction coefficient, depending on the coating material used for the friction pads; nb is the number of the bolts and ns is the number of friction interfaces. This force can be derived knowing the actions on the beam, which has been designed to support vertical loads, and it can be used to derive the minimum required number of bolts for the device. Starting from the friction resistance of the damper, and with the help of an iterative procedure fixing the initial value of some parameters (i.e. the haunch height), all the dimensions of the device can be derived. The second step is the design of the non-dissipative zones (T-stub, L-stub, and haunch, column web in tension and compression and column flange in pure bending) applying the second principle of the capacity design. Therefore, all these components are designed to carry the maximum actions that the damper is able to transfer. Following again an iterative procedure all the joint components are designed according to the EC3 part 1.8 procedures. The original layout of the connection tested in cyclic tests has been slightly modified for the impact test; the reason is linked to the need to maximise the performance of the connection in robustness application or rather when an exceptional event occurs. Compared to the designed connection used in cyclic tests, two main modification have been made: (i) the layout has isolated slotted holes (and not unique long slotted holes) to allow the activation of the maximum available bearing area of all the bolts in shear; (ii) the tested layout is scaled to fit the laboratory facilities, thus the beam-column coupling is rather smaller than the one tested in the other experimental campaign performed. The behaviour of the proposed connection is expected to be suitable in Robustness studies due to the high exhibited ductility, which leads to higher displacement capacity when compared to normal joint solution, and to the possibility of developing catenary actions in the beams. It is worth noting that, obviously, the design principles adopted for robustness could be merged with the seismic design procedures in order to obtain joints able to perform satisfactorily under both load cases.
 |
Fig. (2). Real joint configuration. |
2.2. Component Method Applied to FREEDAM Connections
In order to evaluate the mechanical properties and to extrapolate the moment-rotation characteristic curve of the FREEDAM joint, the component method has been applied. The component approach provided by the Eurocode 3 describes the behaviour of the joint through the knowledge of the mechanical and geometrical characteristics of the joint constitutive components, which can be activated or not, according to the external loading conditions. Each component is characterized by a resistance and a stiffness that combined with the others, lead to the global behaviour of the joint. Through the assembly of the individual constituent components, the moment rotation curve, which represents at each step the applied bending moment and the corresponding rotation of the joint members, can be derived [21]. The codified procedure can be applied to any joint typology following the same principles and rules given for typical connections. The studied connection (Fig. 2) is characterized by a friction damper at the level of the haunch which is not activated until the slippage resistance is achieved; this resistance depends on the material selected for the friction pads and the bolts. In fact, the idea behind the design is the activation of ductile components to ensure a satisfactory performance of the connection under seismic and exceptional loading conditions. When sliding occurs, the bolt is free to move in a slotted hole allowing large rotations in the connection. After the slippage, when the bolts reach the stroke end, new components are activated and an increase of the resistance is obtained due to the occurrence of bearing at the slotted holes. In this specific case the three activated components are: the bolt in shear, the L-stub in bearing and the beam flange in bearing. The activation of these components after the slippage plateaux reduces the initial stiffness of the connection. In other words, the joint behaves differently at different displacement levels, because initially it works as a simple slotted bolted connection (in case of seismic design, small displacements response) and, afterwards it behaves as a kind of bolted double split tee joint activating other ductile components (in case of robustness, large displacements response). The relevant components are listed in Table 1. In the specific tested case, hereinafter described, the design is aimed at bringing the plastic deformation after slippage in the L-stubs in bending for sagging bending moment and in the T-stub in bending for hogging moments. It is worth reminding that EC3 can be used to predict the static behaviour of the proposed connection, thus, it cannot be applied straightforwardly for predicting the behaviour of the joint under dynamic loading.
The real moment-rotation curve can be idealised as two bilinear curves that are describing the behaviour of the joint until the slippage and after. The obtained curve has been used to have a first estimate of the amount of energy potentially dissipated by the joint and to pre-design the impact test. The results of the application of the code procedure to the FREEDAM joint, calculated with the lower and the upper bound of the proposed friction coefficient for the used material, are reported in Fig. (3) for the case of sagging bending moment. The actual behaviour of the connection can be seen as an intermediate between a lower bound and upper bound curve calculated adopting yield or ultimate strength for the materials.
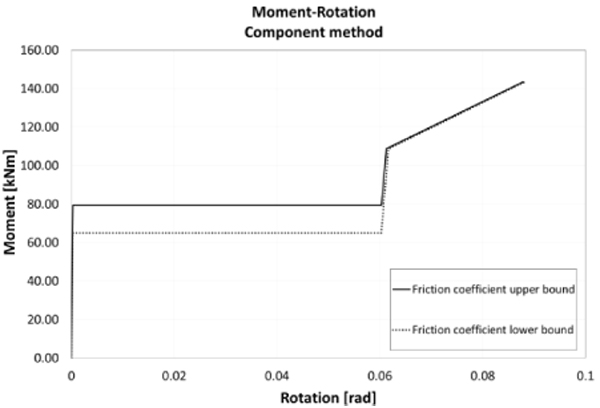 |
Fig. (3). Theoretical moment rotation curve of the tested connection. |
| Relevant Components Sagging | Relevant Components Hogging |
|---|---|
| Components Activated Before The Slippage | |
| Bolt in tension | Bolt in tension |
| Column web in tension | Column web in tension |
| Column flange in bending | Column flange in bending |
| L-Stub flange in bending | T-Stub flange in bending |
| L-Stub web in tension | T-Stub web in tension |
| Components Activated After The Slippage | |
| Bolts in shear | |
| L-stub web in bearing | |
| Beam flange in bearing | |
3. PLANNED EXPERIMENTAL CAMPAIGN
The tested specimens reproduce an internal joint of a steel structure, thus, two beams are connected to a short column by FREEDAM connections. The impact tests will be performed by means of a dropping mass, which will impact the head of the column with a predefined speed. Two main parameters must be considered: the maximum available height of the mass (given by the experimental layout) and the weight of the dropping mass. The system was conceived for previous impact tests performed in the framework of the RobustImpact project [12]. The available equipment is made of a mass equal to 211 kg, which can be increased up to a maximum value, fixed by the capacity of the guide system, and the maximum dropping height equal to 5 m, which has to be considered as not modifiable. These two aspects are strongly related to maximum amount of energy that can be dissipated, and thus, to the achievable value of the bending moment in the connection. The behaviour of the impacted joints compared to their static behaviour will help to highlight the dynamic effects coming from the impact. Two impact tests are planned on the layout presented in the next section, but first, an overview of the results coming from the previous experimental campaign is given.
3.1. Robust Impact as a Benchmark Study
In the framework of the European project entitled RobustImpact, 44 experimental tests on impacted joints have been carried out with the aim of investigating steel and steel-concrete composite building structures under impulsive loading protocols. The main aim of the project was the derivation of design tools and guidelines for predicting the structural response under different scenarios. The experimental campaign is made of 22 tests on beam-to-column joints and 22 tests on column bases, more details can be found in [13]. Prior to the impact tests, several static tests have been performed together with the actual mechanical properties of all the key components. Starting from a designed joint, the initial geometry was changed to reach failure in different components and components 4-5 tests were made for each configuration for a total of 22 tests. In Fig. (4) one of the tested configurations is presented, the EPB specimen, where the acronym EPB indicates the associated failure mode namely the end plate in bending.
 |
Fig. (4). Layout of the EPB connection. |
Different level of energy was chosen for the impact (small, medium and high levels), playing on the combination of mass weight and height. Comparing this results with the ones obtained with the quasi-static tests, the dynamic phenomenon can be recognized and studied. For one of the studied configuration, the four performed test are reported below:
- TEST 1: Dropped mass = 211 kg – Dropping height = 85 mm;
- TEST 2: Dropped mass = 211 kg – Dropping height = 1910 mm;
- TEST 3: Dropped mass = 211 kg – Dropping height = 3000 mm;
- TEST 4: Dropped mass = 167 kg – Dropping height = 3000 mm.
The complete procedure for the prediction of the ratio between Mu,dyn (maximum bending moment appearing during the impact test) and Mu,stat (equivalent static bending moment) can be found in [22]. In Fig. (5) the procedure to calculate the dynamic and static bending moment is schematically reported. In the figure ϑperm is the permanent deformation after the impact and ϑmax is the maximum measured rotation, knowing the initial stiffness of the joint from the static test, it is possible to obtain the value of Mu,dyn, while Mu,stat can be measured using the static curve.
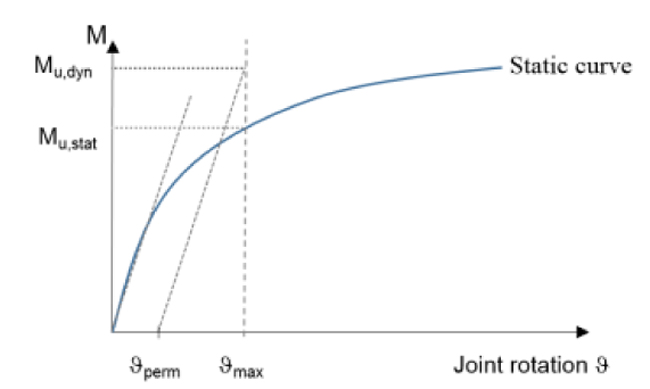 |
Fig. (5). Determination of dynamic and static moment. |
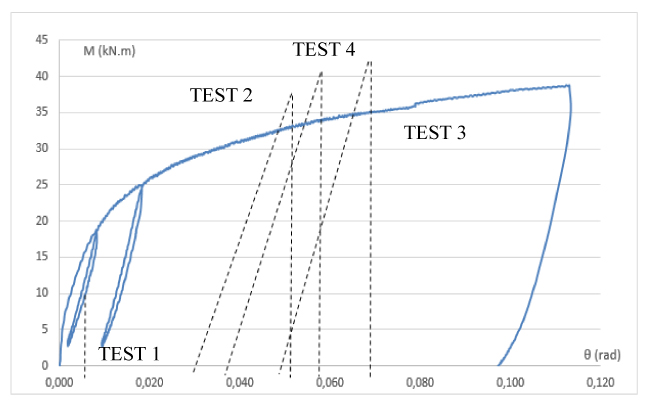 |
Fig. (6). Results for EPB impact tests. |
The ratio between the two obtained bending moments allows to have a first estimate of the strain rate influence on the components. For value of the ratio close to 1 no influence of the strain rate can be observed, while for value higher than one the strain rate is influencing the response of the component. The results obtained for the four presented tests are reported in Fig. (6)
The strain rate effects can be highlighted for test 2, 3 and 4, for which the ratio between the dynamic and the static moments varies between 1,14 and 1, 2. Mainly the same conclusions can be derived for almost all the studied tests. As a general statement, all the performed tests showed a resistance under dynamic loads higher than the corresponding static one and this is linked to the strain-rate sensibility or viscoelasticity. In the same work also an analytical prediction of the strain rate is made through the estimation of the dynamic increase factor (DIF), all the details are reported in [22].
3.2. Geometry of the Tested Joint
The idea behind the planned experimental campaign is the possibility to investigate the behaviour of the proposed connection for robustness application. In fact, this joint is expected to provide significant benefits for robustness studies, provided that ductile components are activated after the slippage. The tested layout is reported in Fig. (7).
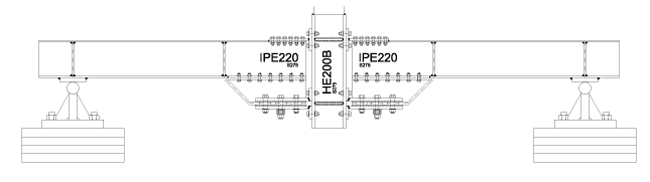 |
Fig. (7). The layout of the impact tests. |
Several observations can be made on the chosen set-up: the length of the column has been defined in order to ensure a good spreading of the transverse compression forces coming from the beam; the length of the beams is governed by the size of the used testing setup, knowing that the spacing between the holes in the strong floor is 50 cm; web stiffeners are placed on the beam, at the position of the beam supports and in correspondence of the haunch, to avoid the buckling of the web under the associated concentrated loads. A 50 mm thick plate is placed at the top of the column, where the mass will impact the specimen, to redistribute the impact load within the column. Starting from the theoretical moment-rotation curve, the mass and the dropping height have been pre-designed using an energetic approach. It is worth to remind that this calculation can be used to have a rough estimation of the dimensions (height and weight of the mass) which will be confirmed or modified according to the results of the static test and of a pilot test.
3.3. Testing Set-Up
The two tests will be performed re-using the available experimental layout realized for the RobustImpact project, however, few modifications have been implemented. The joint achieves higher value of energy (internal energy) compared to the energy dissipated by the available dropping mass, thus, it was necessary to increase the mass. The testing set-up, given in Fig. (8), is a system of tubular guides which are holding and driving the mass. All the measurements (displacements/deformations) will be recorded by two high-speed cameras; one named Baster (400 Hz) and the other Dantec (5000 Hz) are used to catch the global behaviour of the specimen and the local behaviour of key joint components.
3.4. Energetic approach
In order to estimate the height of the dropping mass, the evaluation is made via an energy balance approach. The energy to be absorbed is the kinetic energy plus the additional work done by the weight, W (mass + beam), mainly due to the joints rotations.
With the hypothesis of conservation of Energy, thus, neglecting any kind of friction in the tubular guides of the dropping system, for the scheme given in Fig. (9) it is possible to write:
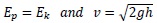 |
(2) |
Where the terms in Eq.(2) are the potential Energy Ep = Mgh and the mass kinetic energy: Ek =
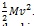 . The external energy (or energy to be absorbed by the specimens) of the system is given by the kinetic energy of the mass and the work of the mass to deform the beam of a fixed value of displacement ymax (or θ max value of the demanded rotation of the joint); this value is chosen according to the value of the target moment to reach in the connection Eq.(3).
. The external energy (or energy to be absorbed by the specimens) of the system is given by the kinetic energy of the mass and the work of the mass to deform the beam of a fixed value of displacement ymax (or θ max value of the demanded rotation of the joint); this value is chosen according to the value of the target moment to reach in the connection Eq.(3).
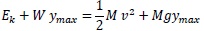 |
(3) |
Applying the Work-Energy principle and considering that the work of elastic deformation in the elastic range is given by
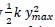 while the work in the plastic range is given by the integration of the moment rotation curve of the joint up to the level of moment to be reached, for both cases the following equation can be written:
while the work in the plastic range is given by the integration of the moment rotation curve of the joint up to the level of moment to be reached, for both cases the following equation can be written:
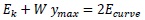 |
(4) |
 |
Fig. (8). Testing setup for the impact tests. |
Physically the work at the second term of the Eq.(4) represents the area under the Moment-Rotation curve of the two joints; the value Ecurve has to be doubled since the right and the left joint absorb the same amount of energy; All the values calculated with the energetic approach are corrected in order to account for the friction of the system. The data extrapolated on the theoretical curve has been verified with the static test results.
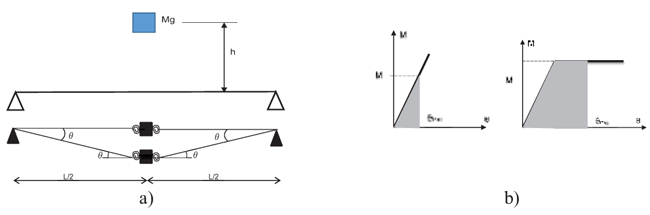 |
Fig. (9). Energetic approach b) Elastic and Plastic energy to be dissipated. |
3.5. Static Test
A preliminary static test has been performed in the laboratory of the University of Liège. The idea was to test the same layout of the impact, consequently, an internal joint with two simply supported beams has been subjected to quasi-static load protocol up to failure. The load has been applied downwards, in order to obtain a sagging bending moment in the joints (Fig. 10).
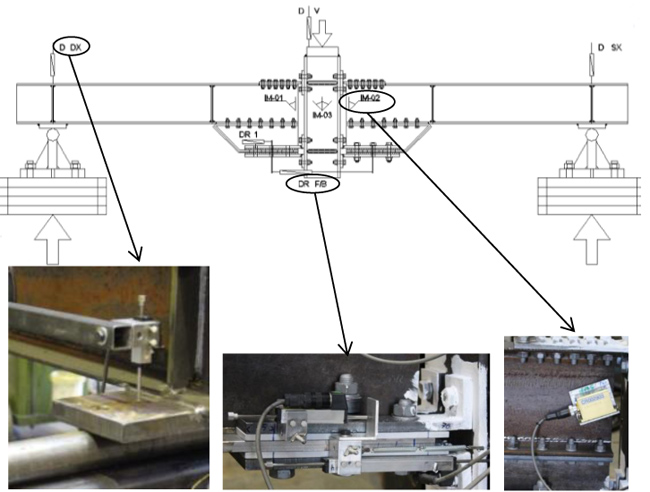 |
Fig. (10). Static test layout and measurements. |
During the test several measurements were taken: the relative rotation of the two joints and the rotation of the column using three inclinometer (IM-01, IM-02, IM-03), the absolute displacements of the supports (D DX and D SX), the vertical displacement (D V), the relative displacements between the external plate and the haunch on both sides (DR 1-DR 2) and the relative displacements between the two haunches of the devices on both sides (DR F/B). All the displacements were measured by means of haunches a piezo-metric indicator. The behaviour of the specimens shows the activation of new components after the slippage of the plate (around 100 kN) which leads to an increase of resistance, until the slippage of the upper T-Stub occurs; the resistance continues growing until the tests ended due to the occurrence of an unexpected global out-of-plane instability of the specimen. The obtained curve is given in Fig. (11), where the applied force and global vertical displacement are reported, removing the beam deformation.
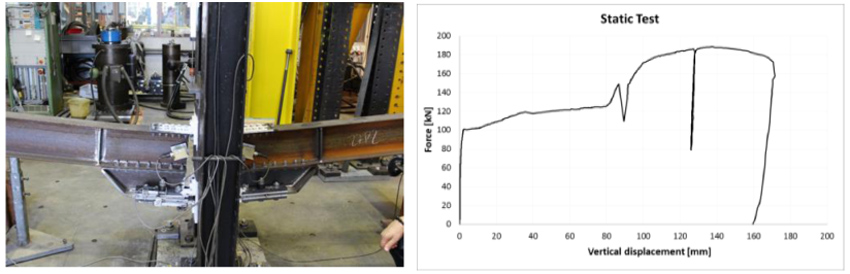 |
Fig. (11). Static test result. |
The application of the component approach presented in section 2.2, although simplified, gave a reasonable estimate of the behaviour of the proposed connection (Fig. 12), thus the pre-design of the impact based on the theoretical behaviour of the joint can be considered reliable.
Starting from this first results, an estimate of the amount of energy dissipated by the connection can be derived. However, an impulsive loading may increase the resistance of some components, as already highlighted in the benchmark study, additionally, the strain rate could also affect the ductility. Clearly, the dynamic tests are needed to better understand all these phenomena.
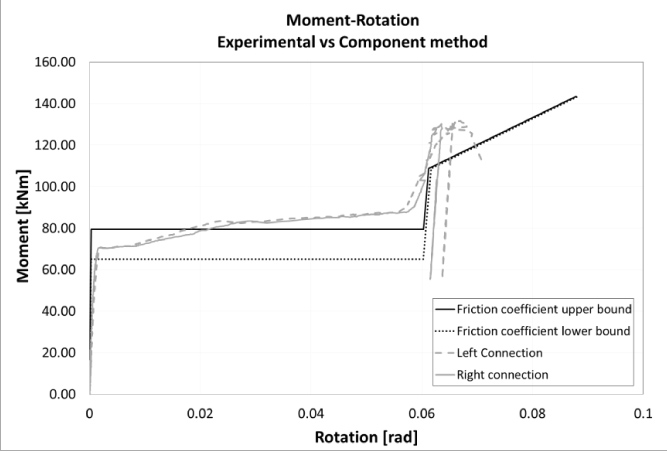 |
Fig. (12). Comparison between theoretical model and experimental results. |
4. CONCLUSION AND FUTURE DEVELOPMENTS
The aim of the planned experimental campaign is to highlight the influence of strain rate effects on the joint response. In fact, it is already known from past works, that strain rates can influence significantly resistance and ductility of connections under dynamic actions. Starting from previous studies, this work aims at deriving a global approach to account for the dynamic effects affecting the response of the FREEDAM connection. From the performed static tests, a first estimate of the behaviour up to the failure of the connection was derived together with the energy dissipated by the joint, which is an input data for impact tests. However, the dynamic response and the dissipated energy can variate under dynamic conditions, as repeated several times and as reported in different works. The final goal of the planned campaign is to identify this possible variation and to properly account for it in the design of the connection.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The study herein is part of the ongoing Project FREEDAM which have been founded by the European Community by research grant RFSR-CT-2015-00022. The support of the European Commission on on RFCS Research & Innovation is gratefully acknowledged








