RESEARCH ARTICLE
Experimental Behavior of Concrete Columns Confined by Transverse Reinforcement with Different Details
Mariateresa Guadagnuolo1, *, Alfonso Donadio2, Anna Tafuro1, Giuseppe Faella1
Article Information
Identifiers and Pagination:
Year: 2020Volume: 14
First Page: 250
Last Page: 265
Publisher ID: TOBCTJ-14-250
DOI: 10.2174/1874836802014010250
Article History:
Received Date: 06/03/2020Revision Received Date: 08/05/2020
Acceptance Date: 18/05/2020
Electronic publication date: 24/08/2020
Collection year: 2020

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
Most of the existing reinforced concrete buildings often have columns with poor transverse reinforcement details. Models for computing the confined concrete strength were developed using experimental tests performed on specimens with transverse reinforcement typical of seismic design. The paper presents the results of an experimental program performed to investigate the effect of type, amount and pitch of transverse reinforcement on the behavior of confined concrete.
Aim:
The paper is also aimed at evaluating whether the current code models are suitable for estimating the confined strength of concrete in existing buildings.
Methods:
A total of 45 reinforced concrete columns with four volume ratios of transverse reinforcement were tested under axial loads. Type and pitch of transverse reinforcement typical of existing r/c buildings not designed according to seismic standards were considered. Therefore, columns reinforced by spiral and hoops with 135° or 90° hooks at the end are investigated for comparing their behavior. The confinement of spirals and hoops to core concrete is discussed as the amount of transverse and longitudinal reinforcement varies. Small increases in strength due to the concrete confinement were measured for hoop pitch of 150 mm (ranging between 2% and 7%), but also for hoops with 90° hook and pitch of 75 mm. Greater increments were obtained by spirals and hoops with 135° hook in the case of 75 mm pitch and when rhomboidal hoops or cross-ties were arranged in addition to the perimeter hoops. A comparison with some similar experimental results is also performed, achieving quite similar results. The mean experimental stress-strain curves are also analyzed.
Results:
The results show how the increase in concrete strength due to the confinement is more dependent on the transverse reinforcement pitch than the type and detail of transverse reinforcement or even less diameter of longitudinal bars. Finally, the experimental strength of confined concrete is then compared with the values provided by Eurocode 8 and the new Italian Building Code, showing that the higher the volumetric percentage of transverse reinforcement, the greater the overestimation of code models.
Conclusion:
An overestimation of codes up to 30% is assessed, systematically lower in the case of spirals, and higher in the case of hoops with 90° hooks at the end. The results highlight the need to develop specific equations to determine the strength increase due to the concrete confinement in the case of existing buildings with poor transverse reinforcement.
1. INTRODUCTION
The assessment of the seismic vulnerability of existing buildings is a priority in large areas of the world [1, 2] since it is the first step for evaluating structural retrofit needs [3-6]. Masonry structures traditionally form the main part of historical centers, but reinforced concrete buildings have recently become a significant part of the built heritage [7]. The seismic analysis of existing building structures needs proper modelings based on experimental tests for defining the values of the main parameters that influence the response under earthquake [8-10].
The seismic behavior of reinforced concrete structures is highly dependent on ductility in plastic hinge regions of columns. Place and extension of hinges in framed structures are key issues mainly in near-fault seismic sites [11, 12]. The most important issue is the provision of sufficient transverse reinforcement to confine the compressed concrete and prevent buckling of longitudinal bars. The confinement of concrete results, in fact, in a significant increase in strength and ductility [13, 14]. The effectiveness of transverse reinforcement in confining concrete depends on both the amount (diameter and pitch) and arrangement (number of cross ties and type of hooks at the end) of the hoops. The hoop configuration is usually satisfactory in new buildings, also because it is strongly required by the seismic regulations in force, while it is often unsatisfactory in most existing buildings, built without special attention to seismic actions [15, 16].
The concrete confinement has been studied for almost a century. The first results were presented by Richart in 1928 [17, 18] and became the reference for many subsequent analytical models [19, 20]. In the following years, several stress-strain models were proposed for confined concrete [21]. The first branch usually was a parabolic curve up to the stress peak, the second branch was frequently linear; a third horizontal branch was sometimes envisaged for accounting the residual stress. In some proposals, the ascending branch did not depend on the confinement [22], whereas in other relationships it depended on both hoops and longitudinal reinforcement [23]. Starting from previous models, Cusson and Paultre [24] and Yong et al. [25] provided stress-strain curves for high-strength concrete; also, Suzuki et al. [26] specifically provided stress-strain curves for square columns only.
In 1980, Sheikh and Uzumeri [27] proposed the concept of “effective confinement area” to consider the confinement effect of square stirrups. Later, Mander et al. [28] systematically investigated the behavior of confined concrete and proposed a single equation for defining the stress-strain behavior of circular, square and rectangular cross-sections. This model is currently regarded as the cornerstone for the research on confined concrete and has been taken up by some Building Codes [29, 30]. Subsequently, several models were proposed as an extension of Mander’s model [31-42]. Other authors, more recently, have proposed different models for estimating the compressive strength of normal and high-strength confined concrete [39, 43-46], also of columns confined by FRP [46-51].
Most of the above models were developed using experimental tests performed on specimens with transverse reinforcement typical of seismic design. The existing r/c buildings, instead, are characterized by a different arrangement of transverse reinforcement, typical of the construction period. In particular, they often have a rather large hoop pitch and hoops with 90° hooks at the end and not 135° hooks. Recently, the new Italian Building Code [52] has imposed the ductility verification of r/c elements also for existing structures and introduced a model for the confined concrete, taken from a previous proposal of Eurocode 8 [29], to be used if the post-peak branch of the stress-strain curve is of more importance.
The main aim of this paper is to present the results of an experimental program performed to investigate the effects of some variables, such as type, amount and pitch of transverse reinforcement and hoop detail, on the behavior of confined concrete. Spirals and hoops with 135° or 90° hooks at the end were used as transverse reinforcement to verify the influence on the column response. The experimental stress-strain curves are then compared with the equation advised by Eurocode 8 and Italian Building Code [29, 30]. A comparison with other experimental results is also performed.
2. MATERIALS AND METHODS
2.1. Tests Concerning the Influence of Hoop Detail
Experimental tests that have been carried out in recent decades investigated the main parameters influencing the confinement of concrete and its mechanical behavior, but most theoretical and experimental researches mainly concerned the typical reinforcement arrangement of new structures. Historically, the tests on reinforced concrete columns can be divided into monotonic and cyclic tests. The oldest ones refer only to the application of vertical loads, while from 1964 onwards, due to the issue of seismic regulations, tests under vertical and horizontal loads were frequently performed.
Most of the authors studied the influence of the volumetric ratio of transverse reinforcement and the geometry of specimens on the confinement effect [53-74], mainly varying sizes of columns and amount of longitudinal and transverse reinforcement. The test set-up was also changed, and some cues were used in the tests illustrated in this paper.
Tables 1 and 2 show the results of some experimental researches that have been performed in recent years on reinforced concrete columns with circular and square cross-sections respectively, in which the confinement effect due to transverse reinforcement was evaluated. In the tables, in addition to the geometry of the specimen cross-section and the hoop type, the volumetric ratio ρw of transverse reinforcement and the ratio fcc/fc of the confined to the unconfined concrete strength are shown.
Most of the tests involve samples of small size (cross-section and height), but with ratios ρw covering a wide range of values. Similar increases were computed for circular and square cross-sections. The increase in confined concrete strength, obviously proportional to the amount of transverse reinforcement, is frequently lesser than 20%, except for some tests in which it is greater with values ranging between 30% and 45%.
The role of the hoop end detail was investigated [61] comparing the response of specimens reinforced with welded hoops to that of specimens reinforced by hoops with 135° and 90° hooks and the end. The tests concerned 1200 mm high specimens with 180 mm square section and 420 mm high steel collars at both ends. The specimens were confined by D6 hoops with spacing ranging between 52 and 90 mm. The volumetric ratio of transverse reinforcement and the corresponding increment in concrete strength are presented in Table 2. A study highlights [61] that the hoop end detail does not cause significant differences in the strength of confined concrete but is quite significant for the post-peak descending branch.
Similar results were obtained in another study [62] comparing the response of specimens without transverse reinforcement to that of specimens reinforced by hoops with 135° and 90° end hooks. The tests concerned specimens with 250 mm square cross-section and 800 mm high, confined by D8 hoops with pitch equal to 100, 200 and 300 mm. The relation between the volumetric ratio of transverse reinforcement and increment in concrete strength was investigated in the paper, as reported in Table 2. The computed increments due to confinement were very small, not exceeding 10%.
Larger increments in confined concrete strength were measured in another study [65], testing specimens with 150 mm square cross-section and 400 mm high. The specimens were confined by D6 customary hoops, using four volumetric ratios of transverse reinforcement. The samples were dynamically loaded with three levels of strain rates, obtaining the strength increments synthesized in Table 2.
The influence of the thickness of concrete cover on the confined strength was analyzed in another study [62] through tests on specimens with 185 and 215 mm square cross-sections. The specimens were 1250 mm high, but only the central portion 600 mm high had a square cross-section, while the specimen end had a tapered section. The paper shows how, after the spalling of concrete cover, the decrease in strength is steeper for larger thicknesses of cover.
Recently, some authors performed tests on concrete columns reinforced by FRP [75-78], or on columns in high-strength concrete confined by spirals [66-68]. In particular, in another study [68] two opposing crosswise spirals were used to confine the concrete core and obtain higher performances. The study shows that the double-crossed spiral technique allows, at the same volumetric ratio of transverse reinforcement, to achieve the same concrete strengths but an increase in displacement of about 20%. The behavior of high strength concrete was also studied [26]. Consistent decreases in ductility were observed with increases in the concrete strength because high-strength concrete exhibits less lateral expansion under axial compression than normal-strength concrete due to its higher modulus of elasticity and lower cracks. Consequently, the authors conclude that confinement is less efficient in high-strength concrete.
| Authors |
Column Diameter (mm) |
Hoop Type |
ρw (%) |
fcc/fc |
|---|---|---|---|---|
| Sheikh et al., 1993 [60]. | 356 | 135° hook | 2.30 | 1.45 |
| 1.69 | 1.35 | |||
| 1.15 | 1.16 | |||
| 0.85 | 1.20 | |||
| 1.15 | 1.24 | |||
| 0.85 | 1.33 | |||
| 0.58 | 1.30 | |||
| 0.58 | 1.28 | |||
| 1.69 | 1.37 | |||
| 254 | 135° hook | 2.30 | 1.21 | |
| 1.67 | 1.10 | |||
| 2.23 | 1.40 | |||
| 1.70 | 1.31 | |||
| 1.15 | 1.23 | |||
| 0.84 | 1.03 | |||
| 1.14 | 1.16 | |||
| 0.87 | 1.16 | |||
| 1.70 | 1.35 | |||
| 203 | 135° hook | 1.79 | 1.32 | |
| 1.15 | 1.16 | |||
| 0.86 | 1.03 | |||
| 1.68 | 1.32 | |||
| 0.93 | 1.16 | |||
| 1.15 | 1.21 | |||
| Li et al., 2016 [58]. | 150 | 135° hook | 1.24 | 1.06 |
| 1.24 | 1.08 | |||
| 1.24 | 1.13 | |||
| Nindyawati et al., 2019 [59]. | 150 | 135° hook | 3.04 | 1.45 |
| 1.82 | 1.21 | |||
| 1.30 | 1.09 |
2.2. Experimental Program and Test Set-up
A total of 45 full-scale concrete columns, reinforced with spirals or hoops and longitudinal steel bars, were tested under compression, as shown in Tables 3, 4 and 5: 27 columns had a cross-section 300 mm wide and 250 mm deep, 18 columns were square with 300 mm side (Fig. 1). The columns were about 1300 mm high so that the height of each column was at least four times the maximum dimension of the cross-section. The stress-strain curve of concrete indeed depends on the geometry ratio of specimens. Usually, the maximum stress in the specimen gradually decreases as the ratio of the height to the maximum dimension of cross-section increases and becomes almost constant when this ratio is greater than 4 [69, 70]. This is because the specimen should fail at the middle portion of its height, which is less influenced by the friction at the interface between the ends of the specimen and loading platens.
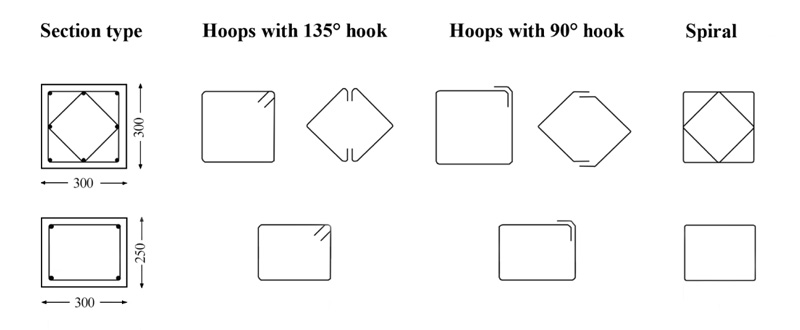 |
Fig. (1). Transverse reinforcement details. |
| Authors |
Cross-section (mm) |
Hoop type |
ρw (%) |
fcc/fc |
|---|---|---|---|---|
| Kato et al., 2006 [61]. | 180 × 180 | 135° hook | 1.05 | 1.09 |
| 90° hook | 1.05 | 1.10 | ||
| 1.05 | 1.34 | |||
| 1.05 | 1.26 | |||
| 1.05 | 1.02 | |||
| 1.05 | 1.04 | |||
| welded | 1.05 | 0.84 | ||
| 1.41 | 1.12 | |||
| 0.82 | 1.00 | |||
| 1.05 | 1.11 | |||
| 1.05 | 0.90 | |||
| 1.05 | 1.09 | |||
| 1.05 | 1.02 | |||
| Campione et al., 2009 [57]. | 165 × 165 | 135° hook | 1.25 | 1.13 |
| 1.60 | 1.36 | |||
| Cosenza et al., 2009 [62]. | 250 × 250 | 135° hook | 0.27 | 1.00 |
| 0.40 | 1.03 | |||
| 0.8 | 1.08 | |||
| 90° hook | 0.27 | 0.97 | ||
| 0.40 | 0.96 | |||
| 0.80 | 1.10 | |||
| Thorhallsson et al., 2012 [63]. | 180 × 180 | 135° hook | 3.15 | 1.13 |
| 3.15 | 1.12 | |||
| 1.57 | 1.22 | |||
| 1.57 | 0.88 | |||
| 1.05 | 0.96 | |||
| 1.05 | 0,89 | |||
| 0.79 | 0.93 | |||
| 5.37 | 1.25 | |||
| 5.37 | 1.39 | |||
| 2.68 | 1.12 | |||
| 2.68 | 1.25 | |||
| 1.79 | 0.99 | |||
| 1.79 | 1.08 | |||
| 1.34 | 0.97 | |||
| Tarabia et al., 2014 [64]. | 150 × 150 | 135° hook | 0.99 | 1.00 |
| 0.99 | 1.15 | |||
| Campione et al., 2016 [21]. | 320 × 200 | 135° hook | 1.44 | 2.22 |
| 1.60 | 0.86 | |||
| Ren et al., 2017 [65]. | 150 × 150 | 135° hook | 0.95 | 1.27 |
| 1.66 | 1.39 | |||
| 2.61 | 1.55 |
| Column cross section (mm) | Column number |
Column height (mm) |
Column reinforcement | |||||
|---|---|---|---|---|---|---|---|---|
| Longitudinal | Transverse | |||||||
|
Number of bars |
Diameter (mm) |
Type |
Diameter (mm) |
Pitch (mm) |
Ratio ρw (%) |
|||
| 300 × 250 | 7 8 9 |
1265 1235 1285 |
4 | 12 | Spiral | 8 | 150 | 0.572 |
| 300 × 300 | 16 17 14 |
1270 1255 1265 |
8 | 12 | 8 | 150 | 0.873 | |
| 300 × 250 | 4 5 6 |
1240 1240 1255 |
4 | 12 | Hoops with 135° hooks at the end |
8 | 150 | 0.572 |
| 300 × 300 | 13 10 15 |
1265 1250 1260 |
8 | 12 | 8 | 150 | 0.873 | |
| 300 × 250 | 1 2 3 |
1250 1240 1245 |
4 | 12 | Hoops with 90° hooks at the end |
8 | 150 | 0.572 |
| 300 × 300 | 18 11 12 |
1280 1270 1250 |
8 | 12 | 8 | 150 | 0.873 | |
| Column Cross Section (mm) | Column Number |
Column Height (mm) |
Column Reinforcement | |||||
|---|---|---|---|---|---|---|---|---|
| Longitudinal | Transverse | |||||||
|
Number of bars |
Diameter (mm) |
Type |
Diameter (mm) |
Pitch (mm) |
Ratio ρw (%) |
|||
| 300 × 250 | 43 44 45 |
1305 1300 1300 |
4 | 12 | Spiral | 8 | 75 | 1.144 |
| 300 × 300 | 61 62 63 |
1300 1305 1305 |
8 | 12 | 8 | 75 | 1.747 | |
| 300 × 250 | 40 41 42 |
1300 1300 1300 |
4 | 12 | Hoops with 135° hooks at the end |
8 | 75 | 1.144 |
| 300 × 300 | 58 59 60 |
1300 1305 1300 |
8 | 12 | 8 | 75 | 1.747 | |
| 300 × 250 | 37 38 39 |
1300 1300 1300 |
4 | 12 | Hoops with 90° hooks at the end |
8 | 75 | 1.144 |
| 300 × 300 | 55 56 57 |
1300 1305 1300 |
8 | 12 | 8 | 75 | 1.747 | |
2.2.1. Material Properties
All columns were cast with a normal strength concrete according to UNI EN 206:2016 [79]. Table 6 contains the concrete constituents and mix detail. The concrete strength was determined using standard 100×200 mm cylinders. Average compressive strengths ranging between 25.2 and 27.8 MPa were measured after 28-days.
Steel bars D12 and D16 (12 and 16 mm in diameter) were used as longitudinal reinforcement and steel bars 8 mm in diameter as transversal reinforcement. The mechanical properties of steel were determined according to UNI EN ISO 15630-1:2019 [80], and a yield tensile strength of 450 MPa was measured.
2.2.2. Specimens
The transverse reinforcement consisted of spirals or hoops. Hoops with a 90° hook at the end (unsatisfactory hoops) [67] and hoops with a 135° hook at the end (satisfactory hoops) were used to build the specimens (Fig. 1). The concrete cover was provided in all the columns, satisfying the minimum cover thickness requirement of 15 mm on the transverse reinforcement. A concrete thickness of about 25 mm was cast between the ends of the longitudinal bars and the top and bottom surfaces of the columns to avoid direct loading on the longitudinal bars.
The columns were divided into three sets. The first two sets had longitudinal steel bars with a diameter of 12 mm and transverse reinforcement with a diameter of 8 mm; the spiral and hoop pitch was equal to 150 mm in the first set (Table 3) and 75 mm in the second set (Table 4). The columns of the third set were reinforced with 16 mm diameter longitudinal bars, 8 mm diameter transverse reinforcement, and space of 75 mm (Table 5). Tables 3, 4 and 5 also show the ratio of the volume of transverse confining steel to the volume of the confined concrete core.
In the following section, the reinforcement of columns is described synthetically using these symbols: D and R identify longitudinal and transverse bars, respectively, and the following number is the diameter of the bar in millimeters. (S), (H) and (U) identify spiral hoops with 135° hooks at the end, and hoops with 90° hooks at the end, respectively. Therefore, 8-D16 means eight 16-mm-diameter longitudinal bars; (S)-R8-75 means an 8-mm-diameter spiral bar with a 75 mm pitch.
2.2.3. Test Set-Up
The tests were performed in the Laboratory of Benecon Scarl and Department of Architecture and Industrial Design of the University of Campania Luigi Vanvitelli. The test equipment consists of a steel structure of four 4.50 m high HEM 300 columns, connected by HEM 300 beams in both the horizontal directions at three different levels. The plan dimension of the loading area is 1.75×1.90 m (Fig. 2).
All specimens were subjected to uniform loading applied by four servo-controlled hydraulic actuators of 1250 kN each, connected to a mobile steel platen, ribbed in both directions. The lower end of the specimen was placed on a stiff steel platen. The specimens were externally confined by steel bolted collars of 8 mm thickness in the end regions to avoid local or early failures in the column end cross-sections (Fig. 2). This technical arrangement, although with different methodologies, was also used in other studies [56, 57, 62, 71, 72].
The specimens were tested under three vertical loading cycles: the first two cycles were used to control that the applied load was centered and to evaluate the response under small loads. The third cycle was performed up to the column failure (Fig. 3). The first two loading cycles were executed in force-control mode with a load speed of 30 kN/sec; the load was increased up to 20% and 40% of the maximum expected strength and then returned to the initial state (one-directional repeated loading). The third loading cycle was performed in displacement-control mode and the column was loaded with 0.02 mm/sec until the end of the test (column failure). The failure was determined by either excessive crushing of core concrete or failure of the transverse reinforcement or buckling of the longitudinal bars (Fig. 4). The application of the vertical load by means of four servo-controlled actuators allowed minimizing the possible effects of eccentric loading due to uneven spalling of concrete cover or failure of longitudinal bars. A sampling frequency of 50 Hz was used in all the loading cycles.
Differential pressure transducers were used to measure the vertical load. The displacements were measured by four linear variable differential transducers (LVDTs) installed at the level of the hydraulic actuators to obtain continuous plots of load-versus-longitudinal displacement of the top surface of the column. Four additional displacement transducers were installed at the mid-height of the column: two in the vertical direction and two in the horizontal direction for measuring the shortening and the lateral deformation of the column. The instrumentation is illustrated in Fig. (2).
| Column Cross Section (mm) | Column number |
Column Heigth (mm) |
Column Reinforcement | |||||
|---|---|---|---|---|---|---|---|---|
| Longitudinal | Transverse | |||||||
|
Number of Bars |
Diameter (mm) |
Type |
Diameter (mm) |
Pitch (mm) |
Ratio ρw (%) |
|||
| 300 × 250 | 52 53 54 |
1305 1305 1300 |
4 | 16 | Spiral | 8 | 75 | 1.144 |
| 300 × 250 | 49 50 51 |
1300 1305 1305 |
4 | 16 | Hoops with 135° hooks at the end |
8 | 75 | 1.144 |
| 300 × 250 | 52 53 54 |
1300 1300 1305 |
4 | 16 | Hoops with 90° hooks at the end |
8 | 75 | 1.144 |
| Cement (Kg/m3) |
Silica (Kg/m3) |
Limestone Powder (Kg/m3) | Fine Aggregate (Kg/m3) | Coarse Aggregate (Kg/m3) | Admixture (l/m3) | Water (l/m3) |
|---|---|---|---|---|---|---|
| 300 | 30 | 250 | 616 | 934 | 5.90 | 175 |
 |
Fig. (2). Column instrumentation. |
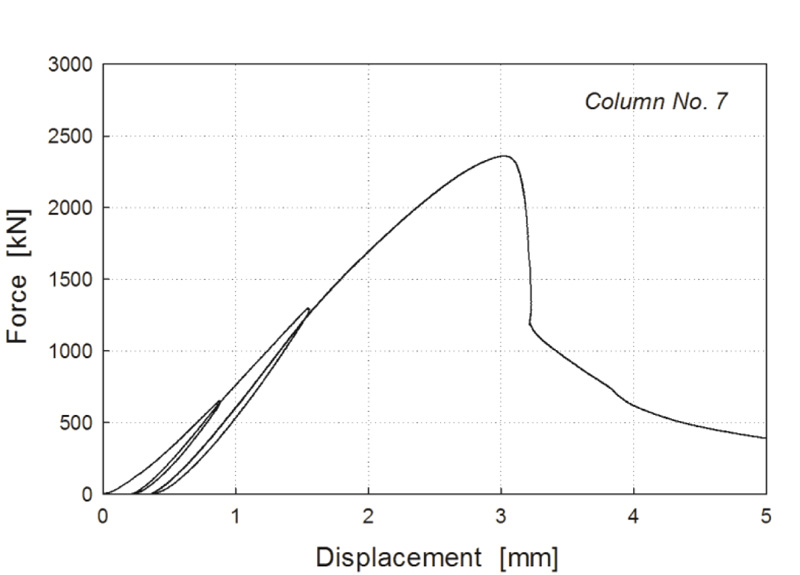 |
Fig. (3). Force-displacement curve of column No. 7. |
3. RESULTS AND DISCUSSION
Fig. (3) shows the load cycles of column No. 7, reinforced with 8-D16 longitudinal bars and spiral 8-mm-diameter with a 150 mm pitch (Table 3). The force-displacement curve has a short initial linear branch and after the maximum force has a steep softening branch and a subsequent small residual capacity, the other columns presented, qualitatively, a similar load-displacement curve.
Damage and failure of some columns, selected as the cross-section and the reinforcement change, are displayed in Fig. (4). The failure due to buckling of longitudinal bars was less frequent in the columns with spirals, and partly in the case of hoops with 135° hooks, than in the case of 90° hooks, where it was often due to both buckling of longitudinal bars and opening (failure) of hoops. The tests also showed that the reduction of the pitch of transverse reinforcement from 150 to 75 mm leads to a lesser tendency of the concrete core to damage, in addition to lower the possibility of the instability of longitudinal bars.
3.1. Force-Displacement Curves
Fig. (5) shows the force-displacement curves, obtained by processing the experimental curve of each specimen and calculating the mean curve for each type of column tested. The green line concerns spiral transverse reinforcement, the red line relates hoops with 135° hooks at the end, and the blue line relates hoops with 90° hooks. In all cases, with increases in displacement, the force gradually increases and after the peak point, the behavior is characterized, even for high values of the volumetric ratio of transverse reinforcement, by a significant decrease in strength to the increase of the mean displacement. The interruption of the curves was sometimes due to the effective column failure, and sometimes due to the need to stop the test at the column failure approaching.
The difference in maximum force in each figure is due to both the larger cross-section of columns (300 × 300 mm vs. 300 × 250 mm) and the different number of cross ties (Fig. 1). The behavior of columns confined with spirals and hoops shows small differences, but those with spirals reach a slightly larger maximum force and displacements. The small influence of the end hook detail of the hoops on the maximum force is also highlighted. However, the efficiency of spirals and hoops with 135° hooks become fundamental in the behavior of reinforced concrete structures when stressed under cyclic loading, like earthquakes, and not under monotonic loading as in the tests of this case. From this point of view, cyclic loading tests confirmed the similar performance of spirals and hoops with 135° hooks [54], but further cyclic tests are needed for endorsing the likely weakness of hoops with 90° hooks.
The softening branch is influenced by several factors such as buckling of longitudinal bars, hoop opening, concrete cracking, and spalling of concrete cover due to instability of longitudinal steel bars. The buckling of the longitudinal bars affected several tested specimens, at larger axial displacements as the hoop pitch decreases. This generally implies that the post-peak behavior was controlled by the instability of the compressed steel bars in specimens with larger hoop pitch (150mm) and by the hoop failure for smaller pitch (75mm). Though, in columns reinforced by hoops with 90° hooks, the concrete cover spalling and the hoops failure was frequently accompanied by the buckling of longitudinal bars.
 |
Fig. (4). Columns failure. |
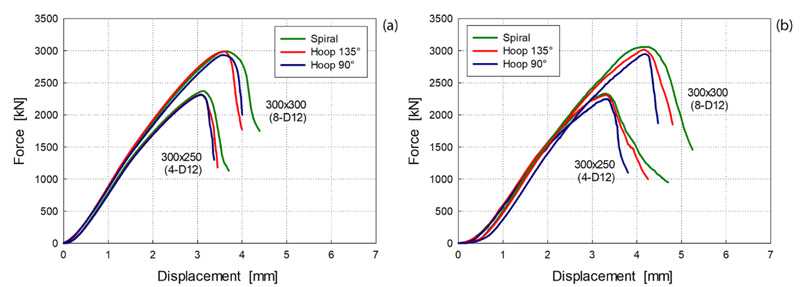 |
Fig. (5). Force-displacement curves for column with 150 mm (a) and 75 mm (b) transverse reinforcement pitch. |
In these conditions, the hoop detail (90° or 135° hooks at the end) is more relevant and the descending branch is steeper in the case of hoops with 150 mm pitch and 90° hooks. After the peak, the transverse reinforcement was occasionally stressed beyond yield, and core concrete and longitudinal bars carried high stresses. At this point, the longitudinal steel bars frequently buckled quickly, sometimes together with the opening of hoops, involving a sudden failure of the column without a stable descending branch. Sometimes the hoops' failure and the buckling of longitudinal bars led to a slightly more stable response at the end of the steeper softening branch due to the greater extension of the specimen damaged area. Moreover, the slope of the softening branch is partly attributable also to a “size effect”: as the displacement increases, the concrete cracks affect a limited portion of the specimen, with an extension almost independent on the specimen cross-section.
Finally, the tests showed that in columns with the same cross-section and transverse reinforcement, the longitudinal reinforcement has a little influence on the response of the columns in terms of concrete confinement.
3.2. Stress-Strain Curves of Confined Concrete
The experimental force-displacement curves were processed to obtain the stress-strain curves of confined concrete (Figs. 6 and 7). The concrete contribution was determined by subtracting the contribution of longitudinal steel bars from the applied force. This contribution was considered to be increasing until the yield strength of the longitudinal bars (450 MPa), and then it became constant.
The stress-strain curves could be then obtained by non-dimensionalizing the above values with respect to the gross concrete area as well as the core concrete area. The gross concrete area should represent the column behavior before the concrete cover starts to spall. The core concrete area should represent the column behavior when the concrete cover is completely spalled. Therefore, the two non-dimensionalized curves thus obtained do not reproduce the response of the column during the spalling of a part of concrete cover. In the following, reference is made, conservatively, to the curves non-dimensionalized with respect to the gross concrete area because the complete spalling of the concrete cover from all four sides of the column did never occur during the tests performed.
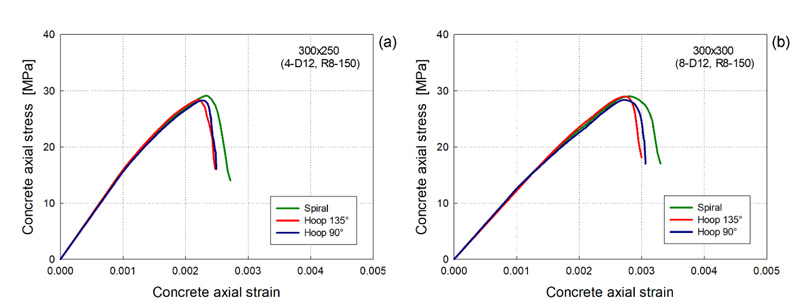 |
Fig. (6). Concrete axial stress-strain curves for column with 150 mm transverse reinforcement pitch. |
 |
Fig. (7). Concrete axial stress-strain curves for column with 75 mm transverse reinforcement pitch. |
Figs. (6 and 7) show the average stress-strain curves obtained with the procedure described above, for columns with 150 mm and 75 mm transverse reinforcement pitch, respectively. It has to be highlighted that the contribution of the concrete confined is not always suitably assessed because it is assumed that the longitudinal bars have a perfectly elastoplastic behavior and that they all yield at the same time. Actually, as the displacement increases, the experimental axial force is due to the contribution provided by the concrete and the longitudinal reinforcement which may differ from bar to bar, depending on the yield and post-yielding strength of each bar. Additionally, it should also be considered that often the instability of a compressed bar can lead to the spalling of a portion of concrete cover, thus altering the contribution of the concrete.
3.3. Effect of the Main Variables on the Confined Concrete Strength
The stress-strain curves of Figs. (6 and 7) allow assessing the dependence of confined concrete strength on type, amount and details of transverse reinforcement. Firstly, it should be remarked that the concrete of the three sets of tested columns (Tables 3, 4 and 5) showed concrete with slightly different unconfined strength, as reported immediately below. This implies that the strengths of the confined concrete are not immediately comparable when they do not belong to the same set of columns, as for the variation of the volumetric percentage of transverse reinforcement. However, Figs. (6 and 7) show that the maximum strength of the confined concrete does not notably depend on the type and detail of transverse reinforcement. The spiral does not result in an appreciable larger strength compared to the hoops with 135° hook at the end, as already highlighted by previous researches [61]. This is due to the low difference in terms of the confinement action provided by spirals and hoops with adequate hooks at the end (135°).
Table 7 contains the mean value of the confined concrete strength for the different types of tested columns. The table also contains the increment ° with respect to the unconfined strength. The latter was assessed by testing cylindrical concrete samples that were cast together with the column casting. The samples with the same days of columns were tested for determining the actual compressive strength of the unconfined concrete. Concrete with specified 28-day cylindrical compressive strength of 25 MPa was envisaged. The compression tests on the samples of the first set of columns provided a mean compressive strength of 27.8 MPa. The second and third sets provided a mean compressive strength of 25.5 MPa and 25.2 MPa, respectively.
The experimental results show a very small confinement effect for the volumetric percentages associated with a hoop pitch of 150 mm. The corresponding increase in concrete strength is smaller than 5%, with values lower than 2% for hoops with a 90° hook at the end. In the latter case, even in the case of a 75 mm pitch, the increase in concrete strength is limited at around 7%.
As expected, the columns with a high volumetric ratio ρw of transverse reinforcement display large concrete strength increments (of about 10-12%) in the case of spirals and hoops with 135° hook at the end. Greater increments (of about 11-16%) were obtained for columns with 300 × 300 mm cross-section where there were also internal rhomboidal hoops or cross-ties with the 75 mm pitch, in addition to the perimeter hoops.
The values of Table 7 also show how the increase in concrete strength due to the confinement, in the examined case, is more dependent on the transverse reinforcement pitch than the diameter of longitudinal bars. The contribution of longitudinal reinforcement to the concrete confinement is indeed rather irrelevant as the bar diameter grows from 12 mm to 16 mm, the strength increases by about 2 to 3 points percent.
The above results are quite similar to those of the few experimental papers [61, 62] that studied columns with similar poor transverse reinforcement in terms of hoop type and pitch (Table 2). Even in these papers, hoops with 90° hook at the end provided an increase in strength of only a few percent. However, the larger comparison for the same volumetric ratio ρw shows that, if ρw increases, the increment obtained by hoops with 90° hook at the end for the tested columns is lower than that of other authors, whereas it is higher for spirals and hoops with 135° hook at the end.
3.4. Experimental Results vs. Theoretical Models
Mander et al. [28] proposed a unified stress-strain curve for confined concrete applicable to all shaped transverse reinforcement. In 2019, the Italian Building Code [30] introduced this model for confined concrete, taking up the equation proposed by the Annex E of Eurocode 8 [29].
The longitudinal compressive concrete stress σc is given by:
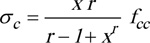 |
(1) |
where fcc is the compressive strength of confined concrete, and parameters x and r are defined as:
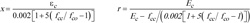 |
(2) |
In Equation (2), fco is the unconfined concrete strength, fcc is the confined compressive strength, Ec the concrete strain, and Ec is the modulus of elasticity. The confined strength fcc is given by:
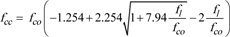 |
(3) |
The confined strength fcc depends on the effective lateral confining pressure fl on the concrete section exerted by the confining reinforcement. According to the approach first proposed by Sheikh and Uzumeri [81], and later modified by Mander et al. [28], the pressure fl is computed as a function of hoops area and pitch, reduced by an efficiency coefficient depending on the ratio between the confined concrete volume and the concrete element volume. Therefore, the pressure fl is computed by:
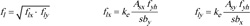 |
(4) |
where Asx and Asy are the total area of transverse bars in x and y directions, s is the pitch of spirals or hoops, bx and by are the core dimensions to centerlines of perimeter hoop, fyh is the yield strength of the transverse reinforcement, and ke is the confinement effectiveness coefficient. The latter can be computed as the product of a term relating to the arrangement of the transverse reinforcement and a term relating to the hoops pitch, through the equation:
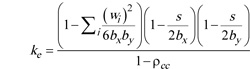 |
(5) |
In Equation (5), wi is the ith clear distance between adjacent longitudinal bars and ×cc is the ratio of the area of longitudinal reinforcement to the area of the core of section.
The model advised by the Italian Building Code is also used in the ductility analysis of existing reinforced concrete structures, where, as previously reported, the columns often have wide pitch hoops and 90° hooks at the end. In this context, it seems interesting to compare the prediction of the code in terms of confined concrete strength with the values obtained experimentally, since the Mander model [28], and then Eurocode 8 [29] and Italian Building Code [30] models, were developed regarding hoops typical of new constructions in a seismic area.
| Cross Section (mm) | Column Reinforcement | Strength | ||||
|---|---|---|---|---|---|---|
| Longitudinal | Transverse |
Ratio ρw (%) |
Mean Confined Strength (MPa) | Unconfined (MPa) |
Increment b° (%) |
|
| 300 × 250 | 4-D12 | (S) D8-150 | 0.572 | 29.10 | 27.80 | 4.68 |
| (H) D8-150 | 28.37 | 2.05 | ||||
| (U) D8-150 | 28.27 | 1.69 | ||||
| 300 × 300 | 8-D12 | (S) D8-150 | 0.873 | 29.99 | 27.80 | 7.88 |
| (H) D8-150 | 28.97 | 4.21 | ||||
| (U) D8-150 | 28.34 | 1.94 | ||||
| 300 × 250 | 4-D12 | (S) D8-75 | 1.144 | 28.56 | 25.50 | 12.00 |
| (H) D8-75 | 28.26 | 10.82 | ||||
| (U) D8-75 | 27.43 | 7.57 | ||||
| 300 × 250 | 4-D16 | (S) D8-75 | 1.144 | 29.22 | 25.20 | 15.95 |
| (H) D8-75 | 28.55 | 13.29 | ||||
| (U) D8-75 | 27.61 | 9.56 | ||||
| 300 × 300 | 8-D12 | (S) D8-75 | 1.747 | 29.78 | 25.50 | 16.78 |
| (H) D8-75 | 29.27 | 14.78 | ||||
| (U) D8-75 | 28.49 | 11.73 | ||||
| Cross Section (mm) | Column Reinforcement | Strength | ||||
|---|---|---|---|---|---|---|
| Longitudinal | Transverse | Experimental (MPa) | Unconfined (MPa) | EC8 (MPa) |
Variation (%) |
|
| 300 × 250 | 4-D12 | (S) D8-150 | 29.10 | 27.80 | 29.39 | 1.00 |
| (H) D8-150 | 28.37 | 3.60 | ||||
| (U) D8-150 | 28.27 | 3.96 | ||||
| 4-D12 | (S) D8-75 | 28.56 | 25.50 | 30.14 | 5.53 | |
| (H) D8-75 | 28.26 | 6.65 | ||||
| (U) D8-75 | 27.43 | 9.88 | ||||
| 4-D16 | (S) D8-75 | 29.22 | 25.20 | 30.07 | 2.91 | |
| (H) D8-75 | 28.55 | 5.32 | ||||
| (U) D8-75 | 27.61 | 8.91 | ||||
| 300 × 300 | 8-D12 | (S) D8-150 | 29.99 | 27.80 | 32.56 | 8.57 |
| (H) D8-150 | 28.97 | 12.39 | ||||
| (U) D8-150 | 28.34 | 14.89 | ||||
| 8-D12 | (S) D8-75 | 29.78 | 25.50 | 37.75 | 26.76 | |
| (H) D8-75 | 29.27 | 28.97 | ||||
| (U) D8-75 | 28.49 | 32.50 | ||||
Table 8 compares the confined concrete strength provided by tests with the value computed through the model advised by Eurocode 8 and Italian Building Code [29, 30]. The confined concrete strength provided by the codes is computed using the effective unconfined strength obtained by testing the corresponding concrete samples, as reported in Table 7. Table 8 also contains the percentage variation of the Eurocode 8 strength with respect to the experimental one. The comparison shows that, with the same transverse reinforcement, the overestimation of Eurocode 8, and therefore of the Italian Building Code, is systematically lower in the case of spirals and higher in the case of hoops with 90° hooks. Therefore, the results show that the code is not fully safe in predicting the compressive strength of confined concrete for the tested columns, representative of those in many existing buildings. This conclusion can also be extended to the results of previous papers [61, 62] that, as previously reported, studied columns with similar transverse reinforcement, reaching similar experimental strengths.
The code overestimation also depends on the volumetric ratio of transverse reinforcement. The experimental tests led to lower strengths than those foreseen by the theoretical model in the case of square cross-section columns, where the volumetric ratio of transverse reinforcement is higher due to the presence of both the perimeter and the rhomboidal internal hoop. In this case, the code overestimation is on average between 10% and 30%, with higher values obviously related to hoops with 90° hooks at the end. Therefore, the results highlight the need to develop specific code equations to compute the strength increase due to the concrete confinement in the case of existing buildings with poor transverse reinforcement. Obviously, the development of a specific new equation requires more experimental tests and numerical analyses than those performed in this paper.
CONCLUSION
The results of an experimental program performed to investigate the effects of type, amount and pitch of transverse reinforcement, as well as of longitudinal reinforcement, on the behavior of confined concrete are presented in the paper. A total of 45 reinforced concrete columns with four volume ratios of transverse reinforcement were tested under axial loads. Columns reinforced by spiral and hoops with 135° or 90° hooks at the end were investigated for comparing their effect on concrete confinement. The hoops with 135° and 90° hooks at the end were used for assessing the differences between stirrups typical of new buildings and hoops recurrent in existing reinforced concrete structures.
The spirals systematically provided slightly higher performance compared to traditional hoops with 135° hook at the end. The columns reinforced with spirals showed slightly higher strength and deformation, and a post-peak branch with a slightly lower slope than that of single hoops with 90° hook. The influence of the hoop details (135° and 90° hook) on the monotonic axial load behavior of columns was limited, as also concluded by other authors in the past. The columns reinforced by hoops with 90° hooks at the end systematically provided slightly less strength than the other stirrup systems tested, but the tests showed a worse behavior in the post-peak phase. However, relevance and efficiency of spirals and hoops with 135° hooks become fundamental in the behavior of reinforced concrete structures stressed under cyclic loading, like earthquakes, and not under monotonic loading as in the tests of this paper. In this context, cyclic loading tests by other authors confirmed similar strength increases in columns of spirals and hoops with 135° hooks, but further cyclic tests are needed for endorsing the likely weakness of hoops with 90° hooks.
The tests showed small increases in strength due to the concrete confinement (ranging between 2% and 7%) for a hoop pitch of 150 mm. Small increases were measured also for hoops with 90° hook, even with the pitch of 75 mm. Increases in the strength of about 10-12% were provided by spirals and hoops with 135° hook in the case of 75 mm pitch. Greater increments (of about 11-16%) were obtained when there were also rhomboidal hoops or cross-ties, in addition to the perimeter hoops and the pitch was 75 mm. The contribution of longitudinal reinforcement to the concrete confinement was rather irrelevant: as the bar diameter grows from 12 mm to 16 mm, the strength increases by a few percent, but failures due to bar instability were reduced.
Finally, the comparison with confined concrete strength provided by Eurocode 8 and Italian Building Code showed an overestimation of codes up to 30%, systematically lower in the case of spirals and higher in the case of hoops with 90° hooks at the end. Besides, the higher the volumetric percentage of transverse reinforcement, the greater the overestimation of code models. The results highlight that the examined building codes are not fully safe in predicting the compressive strength of confined concrete for the tested columns, representative of those in many existing buildings. Therefore, a specific code equation should be developed for computing the confined concrete strength of columns with poor transverse reinforcement, based on more experimental tests and numerical analyses than those performed in this paper.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data used to support the findings of this study are included in the article.
FUNDING
The APC was funded by the “V:ALERE 2019 program” of the University of Campania Luigi Vanvitelli (Italy).
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
For the publication of this article the authors would like to thank the “V:ALERE 2019 program” of the University of Campania Luigi Vanvitelli (Italy) that assigns contributions for the diffusion of open access research products.
The authors wish to thank Arch. Luca Ferri for contribution in the experimental work in-situ. Investigations were performed with equipment kindly provided by Benecon Scarl.








