RESEARCH ARTICLE
Static Analysis of Cross Vaults: The Case of the Cathedral of Casertavecchia
M. Contestabile1, E. Babilio2, *, A. Fortunato3, L. Guerriero1, M. Lippiello2, M. Pasquino2, M. Angelillo3
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
Issue: Suppl 2: M11
First Page: 329
Last Page: 345
Publisher ID: TOBCTJ-10-329
DOI: 10.2174/1874836801610010329
Article History:
Received Date: 15/1/2015Revision Received Date: 15/5/2015
Acceptance Date: 10/7/2015
Electronic publication date: 31/05/2016
Collection year: 2016

open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
In the present paper, on assuming that the material has infinite friction and no cohesion, i.e. it is No-Tension in the sense of Heyman, we study the equilibrium of cross vaults of unequal rise, such as those of some Romanesque and Gothic churches. In particular the case study of the lateral cross vaults of the Cathedral of the old town of Caserta is analyzed. The scope of the paper is not to study in detail and quantitatively any particular vault, rather we give a compressive equilibrium solution (compatible with the unilateral material assumption) for the general case of cross vaults, constructed on arches of unequal rise, and loaded by a uniform load.
For the purpose of the structural analysis, the vault is modelled as a thin shell made of Rigid No-Tension material. The webs of the vault that we consider, are supported on two crossing ribs. To obtain the axial force inside the ribs, equilibrated and singular stress fields (that is stress fields concentrated on curves and balanced with the loads) are constructed.
An estimate of the thrust forces transmitted by the vault to the peripheral arches and walls is also obtained, so that the stability of these structures can be checked.
1. INTRODUCTION
In recent papers by Angelillo et al. ([1-3]), the equilibrium of masonry vaults, domes and helical stairs has been studied, by applying a simplified theory of vaults, put forward in [4].
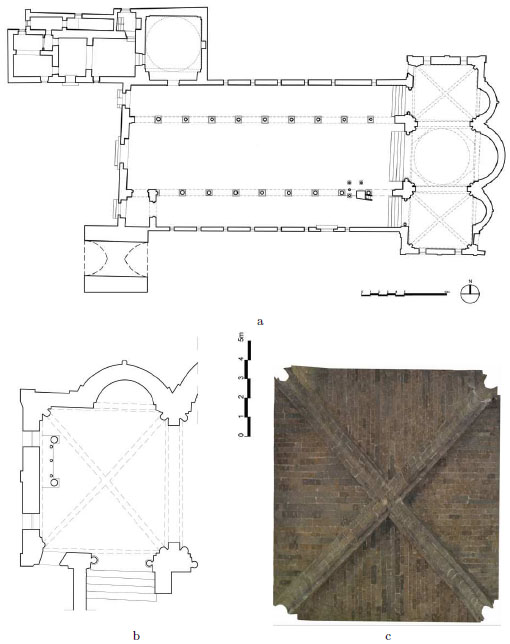
In the present paper by following the same line of thinking (that is on assuming that the material has infinite friction and no cohesion, i.e. it is No-Tension in the sense of Heyman), we shall study the equilibrium of cross vaults of unequal rise, such as those of some Romanesque and Gothic churches. In particular the case study of the Cathedral of the old town of Caserta (Fig. 1a) will be analyzed.
The construction of the Cathedral of Saint Michael in Casertavecchia started under Norman domination, in 1113, and took nearly 40 years to be completed. In 1153, under Archbishop Rainulfo, this Gothic Cathedral was finished, testifying the new identity of the place, which was undergoing a period of expansion and acquiring a new political power.
The Latin cross plan of the church, pointed toward East, shows a neat difference of orientation between the nave and the transept (see Fig. 2a). The form of the transept itself, rather protruded and different in style, suggests that the nave was the original construction.
The church of Saint Michael represents a splendid example of interaction between different traditions, cultural environments and architectural styles, ranging from French-Romanesque style to Sicilian-Arabic influences, testified by elements of Norman-Arabic mould.
 |
Fig. (1). View of the Cathedral in the old town of Caserta, from the bell tower: (a). View of a lateral vault of the transept: (b). |
The facade, whose style is similar to that of the Amalfi Cathedral, shows three white marble portals, nestled into a comparatively large wall and contrasting with the grey-ochre colour of the tuff masonry stones. The gable is marked with five equally spaced blind, interwoven arches, supported by six small marble columns.
The roof of the nave is made with shingles supported by a A-shaped wooden trusses, visible from the interior; the transept is covered by cross vaults of distinct French style, since the stones of the webs are disposed toward the key stone. Another evidence is given by the form and style of the section of the ribs disposed along the diagonals (see Fig. 1b, 2c and [5], p.165).
We suggest the reader inclined toward a historical-structural approach to masonry architecture to read the manual on vaults by Henri Thunnissen [5], which combines the historical interest with practical application and structural insight.
The equilibrium problem that we consider here is represented by the case study represented by the two lateral cross vaults of the transept, shown in Fig. (1b), and whose plan is reported in Fig. (2b). A detailed 3D photographic reconstruction of the intrados of one of the two cross vaults is reported in Fig. (2c).
The scope of the paper is not to study in detail and quantitatively any particular vault, rather we shall try to give a compressive equilibrium solution (compatible with the unilateral material assumption) for the general case of cross vaults, constructed on arches of unequal rise, and loaded by a uniform load.
For the purpose of the structural analysis, the vault is modelled as a thin shell made of Rigid No-Tension material. The vault we consider is supported on two crossing arches, which are called ribs. To obtain the axial force inside the ribs, equilibrated and singular stress fields (that is stress fields concentrated on curves and balanced with the loads) are constructed.
The existence of such (regular and singular) compressive equilibrium solutions, is a proof that, in the spirit of the safe theorem of Limit Analysis, the structure can stand without resorting to tensile strength.
An estimate of the thrust forces transmitted by the vault to the peripheral arches and walls is also obtained, so that the stability of these structures can be checked.
2. The NT MODEL
As a first approximation to the behaviour of the masonry shell that we are studying, the Rigid No-Tension model is adopted. This crude unilateral model material that idealizes the real material as indefinitely strong in compression but incapable of sustaining tensile stresses, is rigid in compression and can elongate freely, a positive deformation of the material being interpreted as a size of fracture into the material (either smeared or concentrated). It must be observed that, though this ideal material has a limited repertoire of admissible stresses and strains and can exhibit fractures, its uniaxial behaviour in elongation is elastic in the sense that strain determines stress and there are no residual strains upon reloading in compression.
The unilateral model for masonry has been around since the nineteenth century (see Moseley [6]), first rationally introduced by Heyman in [7], was divulgated and extended in Italy, thanks to the effort of Di Pasquale [8] and other members of the Italian school of Structural Mechanics, such as Romano & Romano [9], Baratta [10], Del Piero [11, 12], Como [13], Angelillo [14]. Angelillo & Giliberti [15], Angelillo & Rosso [16] and Angelillo & Olivito [17], till the more recent articles of Fortunato [18] and Angelillo et al. [19-22]. A general treatment of internal constraints on stress can be found in [23].
The formulation of the BVP for unilateral masonry materials, that is Rigid No-Tension materials for which the latent strains (fractures) satisfy a normality condition with respect to the admissible stresses, can be found in the recent papers by Angelillo [22], Silhavi [24], Lucchesi [25] and Angelillo [26].
In particular, in the application we present here, we focus on the statical approach, namely on the safe theorem of limit analysis. By working with the safe theorem, one can admit also singular stresses representing concentrated compressive internal forces, with support on surfaces or curves located inside the masonry.
Indeed the more efficient tool that can be introduced for applying the unilateral No-Tension model to masonry structures is the systematic use of singular stress and strain fields, within the framework defined by the two theorems of Limit Analysis (see Angelillo et al. [21] for applications of the safe theorem and Fortunato et al. [27] for applications of the kinematic theorem to walls).
The concept of compatible loads and distortions, and the validity of the two theorems of Limit Analysis, admitting singular stresses and discontinuous displacements, are discussed in Angelillo et al. [21, 26, 27]. The use of singular equilibrated stresses for approximating plane equilibrium problems can be traced to the work of Fraternali et al. [28], and for vaults to the more recent paper by Block & Ochsendorf [29].
2.1. Examples of Singular Equilibrated Stress Fields
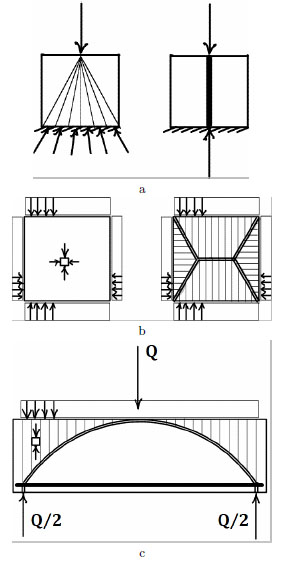
The analysis of some trivial examples of regular and singular equilibrated and compressive stress fields, in the plane case, can help to visualize how singular stresses look like inside the masonry. In Fig. (3), three simple cases are reported. In the example of (Fig. 3a), there is a panel rigidly supported at the bottom base and subject to a vertical concentrated force at the center of the upper base. Two stress fields of pure compression which are both statically admissible for the case considered, are shown.
On the left, a regular state, consisting of a fan of uniaxial compressive stresses emanating from the point of application of the force, is depicted.
On the right, a singular solution for which a constant singular stress is concentrated along the center line is reported. We may think of the support of the singular stress inside the panel as a 1d bar carrying an axial force.
In the mathematical terminology such a stress is a line Dirac delta with support on the center line.
The equilibrium conditions on such singular stress fields can be enforced in much the same way it is done with structures formed by straight and curved bars, that is 1d elements transmitting only axial forces (no moments and no shears), and subject to given external loads. The regular part of the stress field can have the effect of transmitting distributed loads to such ideal structures: if the regular part is discontinuous across an internal line Γ , the loads acting on the ideal 1d structure having the form of Γ , are represented by the unbalanced tractions produced by the regular part of the stress, across this ideal structure.
The second example (Fig. 3b), refers to a traction problem (that is a boundary value problem of pure loading: no constraints), in which there are no concentrated forces applied at the boundary. A regular and a singular stress field balancing the given tractions are reported in Fig. (3b).
A third interesting example is reported in Fig. (3c) . The example is concerned with a rectangular panel loaded by a uniform load at the upper base, supported by two vertical forces at two points on the lower base, and representing a concrete beam reinforced by a lower straight rebar and with no stirrups. In the statically admissible stress field that is depicted in Fig. (3c), the reinforcing steel, simulated in this 2d example by a 1d straight fiber, carries a singular stress, that is a concentrated constant tensile axial force; the stress field in the concrete consists of a singular part, represented by a (variable) concentrated compressive axial force, applied on a curved arch, and a regular part, represented by vertical uniaxial stresses located above the arch, and by vanishing stresses below it.
2.2. Singular Stresses as Line Dirac Deltas
Calling T the stress field inside the body, for linear elastic materials, that is hyperelastic materials for which the elastic energy is a quadratic function of stress, the usual assumption is that
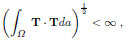 |
that is, stress fields that are square-summable are admitted. For RNT materials a weaker assumption can be made, namely
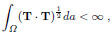 |
that is, one can admit stress fields that are only summable. Therefore the set of competing functions enlarges to bounded measures, that is to summable distributions 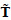 :
:
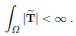 |
We note that line Dirac deltas are special bounded measures.
In general, bounded measures can be decomposed into the sum of two parts
| T͂ = T͂r + T͂s , |
where 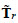 is absolutely continuous with respect to the area measure (that is
is absolutely continuous with respect to the area measure (that is 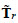 is a density per unit area) and
is a density per unit area) and 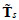 is the singular part.
is the singular part.
For simplicity only bounded measures 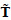 whose singular part is concentrated on a finite number of regular arcs, that is bounded measures admitting on such curves a density
whose singular part is concentrated on a finite number of regular arcs, that is bounded measures admitting on such curves a density 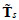 with respect to the length measure, are usually considered. This restricted class of distributions, called line Dirac deltas, represent the distributional derivatives of functions belonging to a subset of the function space BV (the space of functions of Bounded Variation), called SBV (the space of function of Special Bounded Variation), that is the space of functions of Bounded Variation whose Cantor part is void (for reference to such space and other issues connected with free discontinuities, the reader can consult the book by Ambrosio, Fusco, and Pallara [30] and see the papers [31-33]).
with respect to the length measure, are usually considered. This restricted class of distributions, called line Dirac deltas, represent the distributional derivatives of functions belonging to a subset of the function space BV (the space of functions of Bounded Variation), called SBV (the space of function of Special Bounded Variation), that is the space of functions of Bounded Variation whose Cantor part is void (for reference to such space and other issues connected with free discontinuities, the reader can consult the book by Ambrosio, Fusco, and Pallara [30] and see the papers [31-33]).
3. ANALYSIS
3.1. Geometry
The relevant geometrical dimensions of a vault are the geometry of the intrados and extrados surfaces, its (possibly variable) thickness t, the geometry of the fillings, and for vaults supported on arches rising from piers, the form and dimension of the enlargements (counter-sinks) of the piers at their tops. A schematic perspective view of a cross vault with ribs is depicted in Fig. (4a).
It is assumed that the load applied to the vault is carried by a shell structure S of thickness t′. The geometry of the shell S is not fixed, in the sense that we can displace and distort it, provided that we keep it inside the masonry.
The shell surface S carrying the stress is defined a la Monge, by considering as parameters the x1, x2 components of the points of S, and defining the third component as x3 = f (x1, x2), f being a continuous function of its arguments. The orthonormal triad associated to the Cartesian reference system depicted in Fig. (3b) is denoted {ê1, ê2, ê3}.
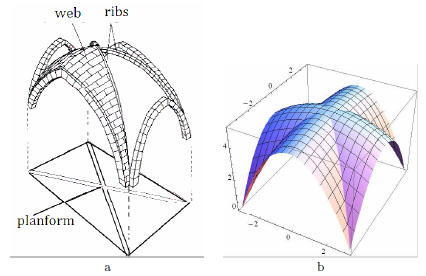 |
Fig. (4). 3D view of a gothic groin vault: (a). 3D view of the surface S: (b). |
The couple (x1, x2) belongs to a connected 2d domain Ω, called the planform of the membrane S. Ω is a domain whose boundary ∂Ω is a closed, plane curve of finite perimeter, endowed (a.e.) of a unit outer normal n, contained in the plane {O; x1, x2}.
The surface that we consider is continuous but not necessarily smooth. A 3D view of such a surface structure, that could be fitted inside the masonry for the case of Fig. (4a), is depicted in Fig. (4b).
By denoting {•, •, •} the components of vector quantities with respect to the Cartesian frame shown in Fig. (4b),the parametric description of the surface S is
| x(x1, x2) = {x1, x2, f (x1, x2)} . | (1) |
The natural (covariant) base vectors associated to the curvilinear system defined on S by the couple (x1, x2), are
| a1 = {1, 0, f,1} , a2 = {0, 1, f,2} , | (2) |
where a comma followed by an index, say α, stands for differentiation with respect to xα. The unit normal to S (also called m in what follows) is defined as
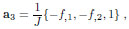 |
J = (1 + f,21 + f,22)1/2 being the Jacobian determinant, that is the ratio between the differential surface area and its projection on the planform.
The covariant components gαβ of the metric tensor, defined by the relations
| gαβ = aα • aβ |
are, in this case
| g11 = 1 + f,21, g12 = g21 = f,1f,2, g22 = 1 + f,22 . |
Finally, the reciprocal (contravariant) base vectors are
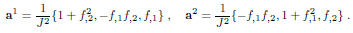 |
3.2. Membrane Equilibrium
The generalized membrane stress on S, is defined by the (surface) stress tensor T. In the covariant base, by adopting summation convention on repeated Greek indexes: α, β, γ, ... = 1, 2, it can be represented as follows:
T = Tαβ aα
 aβ aβ
|
Tαβ being the contravariant components of T. Notice that the basis {a1, a2} is neither unit nor orthogonal, then though the contravariant components are useful and convenient, they are non-physical components of stress, and a bit of conversions is needed to transform them into Cartesian stress components.
Membrane equilibrium is dictated by the condition that the divergence of the generalized surface stress T balances the load b, defined per unit surface area on S. Such a condition can be written, explicitly, as follows:
 |
(3) |
The most simple way of thinking about membrane equilibrium of a thin shell under a load p defined per unit projected area:
| p = {p1, p2, p3} , |
(that is p = Jb) is to adopt Pucher’s approach (see [34]). With Pucher’s transformation the generalized contravariant stress components Tαβ on the surface are transformed into projected stress components Sαβ = JTαβ in the planform (J being the Jacobian of the coordinate transformation and, as already remarked, the ratio between the surface differential areas on the surface and on the planform). Indeed, by projecting equation (3) into the three non-coplanar directions {ê1, ê2, m = a3}, after some algebra,one obtains:
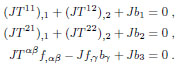 |
Therefore, on substituting for the projected stress components Sαβ and for the load per unit projected area p, one obtains:
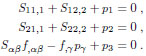 |
(4) |
The equilibrium equations (4), in terms of such projected stresses, in the plane of the planform, are identical to those of the plane problem and, in the case of pure vertical loading (say p = {0, 0, −p}), may be solved with the use of an Airy stress function F , in the form:
| S11 = F,22 , S22 = F,11 , S12 = −F,12 , | (5) |
F being a function of x1, x2, usually assumed as smooth, and that here we consider only continuous. Indeed if F is only continuous, it may have folds, and, along these folds, the projected stress (and hence the actual stress) is a line Dirac delta with support along the projection Γ of the fold on the planform Ω. The Hessian of F is singular transversely to Γ (namely has a uniaxial singular part directed as the normal to Γ ); the intensity of the concentrated second derivative component in the direction of the normal h to Γ , is represented by the jump of the directional derivative of F in the direction of h, called [F] h. Therefore, the singular part of the Hessian H of F can be written as:
Hs = δ (Γ ) [F ] hh
 h , h ,
|
δ(Γ ) being the unit line Dirac delta defined on Γ .
Based on relations (5), the singular part of the corresponding projected stress is also a line Dirac delta defined on Γ , uniaxial in the direction of the unit tangent k to Γ :
Ts = δ(Γ ) [F ]hk
 k , k ,
|
The force acting transversely to the surface S, is balanced by the scalar product of the matrix of the Pucher stress components times the matrix of the covariant components of the curvature (see the third of equations (4)). In terms of the Airy’s solution, for the case of pure vertical loading, such transverse equilibrium equation can be rewritten in the form
| F,22f,11 + F,11f,22 − 2F,12f,12 = p . | (6) |
The first to consider membrane equilibrium with Pucher's transformation for NT materials were Angelillo & Fortunato in [4]. If the membrane is made of NT material, the surface stress tensor must be negative semi-definite and (as it is shown in [4]) the matrix itself of the projected stresses must be negative semi-definite. In terms of the stress function F , this condition can be translated into the two conditions:
| F,11 + F,22 ≤ 0 , F,11F,22 − F,12F,21 ≥ 0 , | (7) |
that is F must be concave.
3.3. Equilibrium of the NT Membrane in Terms of F
Based on the Airy solution (5), in the case of pure vertical loading, the problem of equilibrium for the unilateral membrane S reduces to the form:
Find a concave stress function F satisfying equation (6), with the boundary conditions:
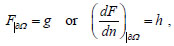 |
(8) |
where g and h are the moment and the shear force along a 1d beam structure, having the same form of the projected boundary, and loaded by the projected tractions acting at the boundary.
Remark. Equation (6) is a second-order p.d.e. rather than a fourth-order one (like in plane linear elasticity); therefore, we cannot impose both boundary conditions. As a result, we must choose between prescribing either the projection of the normal stress component at the boundary (i.e., to give F ) or prescribing the tangential component (dF/dn given).
If the shape f is given, then the second-order differential equation (6) with the BCs (8) has a unique solution for F (modulo a linear function not affecting the corresponding stress). Therefore, for a given shape one can just verify, aposteriori, if the solution corresponding to that shape is or is not concave.
The idea is that a concave solution F could be produced, by changing f within the masonry, that is, allowing for the surface S to vary: in a sense, under this view, the problem of equilibrium of a unilateral membrane resembles the problem of equilibrium of a cord or a net of cords under given loads: the cord and the net are underdetermined structures that change their geometry in order to reach equilibrium (form finding).
Another possible approach to obtain an admissible stress field is to consider f as an unknown, and start from a class of statically admissible and concave Pucher stresses, by assigning a restricted class of concave stress functions F (notice that this can be done, since the planform equilibrium equations are independent of the shape). Then determine, by solving the p.d.e. of transverse equilibrium, a corresponding restricted class of shapes f , and check whether the corresponding S can fit inside the vault.
Some iterative procedures based on the alternate applications of this two dual approaches starting from f or from F, are proposed and exploited in a recent paper (see [1]) in the case of domes. Here we use simply the approach based on the assignment of a restricted class of stress functions F.
4. EQUILIBRIUM OF A NT CROSS VAULT: A CASE STUDY
4.1. Geometry of the Surface S for a Cross Vault
The relevant geometrical dimensions of a generic cross vault are the internal spans a, b, the rises h1, h2 of the supporting arches, and the rise h of the center of the vault. The, possibly variable, thickness t of the vault is another important parameter. An element whose definition is of crucial importance, is the geometry of the fillings together with the form and dimension of the enlargements (counter-sinks) of the piers at their tops. A schematic 3D view of the intrados of a cross vault is depicted in Fig. (5a), to which we refer for notations.
It is assumed that the load applied to the vault is carried by a shell structure S of thickness t′. The geometry of the shell S is not fixed, in the sense that we can displace and distort it, provided that we keep it inside the masonry.
We describe the shell surface S a la Monge, in the form (1), that is in terms of a continuous function f depending on x1, x2. For the surface S, we assume:
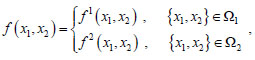 |
(9) |
{Ω1, Ω2}, being the partition of the planform Ω of S, shown in Fig. (5a).
The surface that we consider is continuous but not smooth; it is divided into four curved sectors, meeting at an angle at the common boundaries. In doing this we follow the geometry of the intrados of the vault, and, as we shall see, allow for concentrated forces along the ribs. The geometry of the ribs (shown by thick solid lines in Fig. 6a), treated as 1d arches, is defined by the intersection of these surfaces. A schematic 3D view of such a folded structure S is depicted in Fig. (4b).
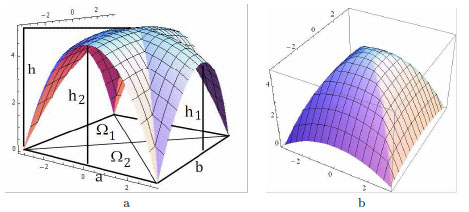 |
Fig. (5). Schematic 3D view of the intrados of a cross vault: (a). Quadratic, continuous and folded, stress function F, corresponding to the form (7), for a special choice of the parameters:(b). |
4.2. Equilibrium on the Folds of f
For the cross vault shown in Fig. (5a), we then explore the possibility that both S (i.e., f ) and the stress function F are folded on the same line Γ , that is, both the curvature field (i.e., the Hessian of f ) and the stress field (i.e. the Hessian of F ) have singularities in the form of line Dirac deltas having support on Γ .
The fact that when F is folded on a line Γ then also f must be folded on the same line (and vice-versa) can be explained as follows. To fix ideas assume that F,11 is a line Dirac delta along the line Γ = {(x1, x2, 0)
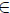 Ω s.t. x1 = 0}, that is the surface whose graph is represented by F is folded and the folding line has a projection on the planform in the form of a straight line directed as the axis x2.
Ω s.t. x1 = 0}, that is the surface whose graph is represented by F is folded and the folding line has a projection on the planform in the form of a straight line directed as the axis x2.
By rewriting the equation of transverse equilibrium (6) along the line Γ
| F,22| Γf,11| Γ + F,11| Γf,22| Γ − 2F,12| Γf,12| Γ = p| Γ , | (10) |
we deduce that, in order to satisfy it, point by point, along Γ , either
- f,22| Γ = 0, that is, the line on S that projects on x2 is straight;
- p is singular along Γ and cancels F,11| ΓF,22| Γ;
- F,11| Γ is singular along Γ (i.e., also S is folded along Γ ) and F,22| Γf,11| Γ cancels F,11| Γf,22| Γ.
Therefore, if the surface S is curved along Γ , and p is absolutely continuous, both F and f must be folded along the same line Γ .
4.3. Transverse Equilibrium Starting from F
To construct a statically admissible stress field for the cross vault, we start by assigning a restricted class of stress functions, depending on a few parameters.
A sensible choice for F is of the type depicted in Fig. (5b). The corresponding Pucher stress is a piecewise constant and singular stress field (the singular part being a concentrated axial force field with support on the diagonals); four balanced concentrated forces, directed as the diagonals and representing the thrust of the diagonal arches, emerge at the corners (see Fig. 7a). The class of stress functions we consider is defined as follows
 |
(11) |
σ, σ1, σ2, being unknown parameters. The surface represented by this composite stress function is represented in Fig. (5b), for a particular value of the parameters, is continuous but folded along the lines ℓ1, ℓ2, whose parametric description is
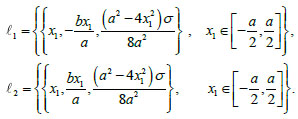 |
The regular part of the stress corresponding to the function F defined in (11) is piecewise continuous. In Ω1
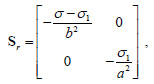 |
and in Ω2
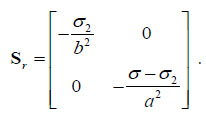 |
Notice that the stress inside Ω1 and Ω2 is negative semidefinite if σ1 ≤ σ and σ2 ≤ σ, a circumstance that is to be verified at the end of the analysis.
Since the surface is folded, then its Hessian is singular along the diagonals of the rectangular planform. The corresponding singular part Ss of the projected stress S associated to F , having support on the two diagonals
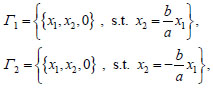 |
is a line Dirac delta, whose intensity can be computed as the jump of slope of F across the diagonals.
Some simple calculation show that, in the present case, the singular stress can be written as follows:
Ss = δ(Γ1) g (σ, σ1, σ2) |x1| k1
 k1 + δ(Γ2) g (σ, σ1, σ2) |x1| k2 k1 + δ(Γ2) g (σ, σ1, σ2) |x1| k2
 k2 , k2 ,
|
(12) |
where,
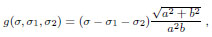 |
and δ(Γ1), δ(Γ2) are the line Dirac deltas with support on the diagonals, k1, k2 the unit vectors along the diagonals.
From (12) we see that the axial internal force, concentrated along the diagonals, is non positive (that is compressive) if
| σ ≤ σ1 + σ2 |
Assuming that the load p is uniform, in order to satisfy the equation of trans-verse equilibrium (6) away from the diagonals (that is where the stress is regular), the shape (9) must be piecewise quadratic. The general solution of these two differential equations (given the restrictions on the shape of S, see Fig. (5a)) is
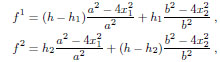 |
(13) |
where h, h1, h2, are the rises of the diagonal and lateral arches, three parameters that we may change slightly with respect to the corresponding actual values at the intrados, in order to fit the surface S inside the masonry.
For the cross vault of Figs. (1b, 2b, 2c), the values of the geometrical parameters appearing in (13), expressed in meters, are a = 6.42m , b = 7.25m , h = 5.10m , h1 = h = 5.10m , h2 = 4.51m .
The form of the surface S corresponding to these values of the parameters, obtained as a solution for the case at hand, is depicted in Fig. (6a). In the same pictures the ribs of the arch are reported with thick, solid lines.
If f is piecewise quadratic and of the form (13), taking into account (11), the equilibrium equation (6), written inside Ω1 and Ω2 (that is excluding the diagonals) gives the two algebraic conditions
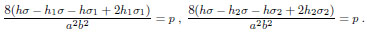 |
(14) |
Besides these two equations, we must also enforce equilibrium along Γ1 and Γ2, that is impose equation (10). In the case at hand, such a condition reduces to the single algebraic equation
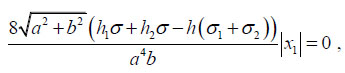 |
that, since must be valid for any value of x1 in the interval [−a/2, a/2], gives the condition
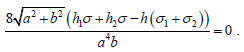 |
(15) |
The system formed by equations (14) and equation (15), is linear in the three unknown parameters σ, σ1, σ2, and admits the unique solution:
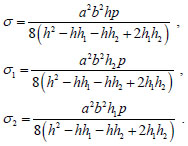 |
(16) |
Notice that, this solution verifies all the conditions that must be imposed on the parameters in order that the stress be compressive, if h1 ≤ h, h2 ≤ h.
Finally, from (11) on the base of (16), stress function which we select to generate a statically admissible stress field is
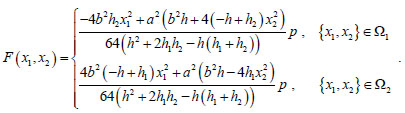 |
(17) |
The 3D plot of this function for a = 6.42m, b = 7.25m, h = 5.10m, h1 = h = 5.10m, h2 = 4.51m is reported in Fig. (6b). It can be observed that, in this special case, the surface of which this F is the graph, is a ruled surface (that is has a single curvature) in Ω2, and is a double curvature surface in Ω1.
4.4. Postprocessing of the Solution Obtained in Terms of F
4.4.1. Projected Stresses and Forces
By recalling (5), the projected stress corresponding to the stress function (17) consists of regular and singular parts Sr and Ss. For what concerns the regular part, in Ω1
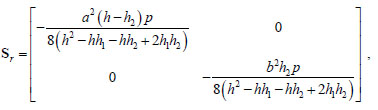 |
and in Ω2
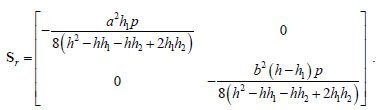 |
Notice that the stress inside Ω1 and Ω2 is negative semidefinite if h1 ≤ h and h2 ≤ h. Schematic pictures of the projected stresses for the general case and for case study, are reported in Figs. (7a, b).
Since the surface is folded, then its Hessian is singular along the diagonals of the rectangular planform. The corresponding singular part of the projected stress S associated to F , having support on the two diagonals Γ1, Γ2, is a line Dirac delta, whose intensity can be computed as the jump of slope of F across the diagonals.
Taking into account (17) and recalling (12), in the present case, the singular stress can be written as follows:
Ss = δ(Γ1)g(h, h1, h2, p) |x1| k1
 k1 + δ(Γ2)g(h, h1, h2, p) |x1| k2 k1 + δ(Γ2)g(h, h1, h2, p) |x1| k2
 k2 , k2 ,
|
where,
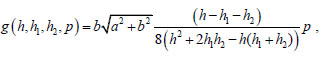 |
and δ(Γ1), δ(Γ2) are the line Dirac delta with support on the diagonals, k1, k2 are the unit vectors along the diagonals.
Then the projection on the planform of the axial contact force transmitted along the two ribs, written as a function of x1 is
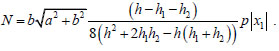 |
(18) |
N is positive if h ≤ h1 + h2.
4.4.2. Physical Stresses and Forces
To pass from projected stress components to physical stress components some transformations are needed.
If we just wish to write the principal stresses Σ1, Σ2 of the regular part of stress T on the surface S, we can compute the first and second invariants i1, i2 of the stress tensor on S and find the two eigenvalues by solving the equation
| Σ2-i1Σ + i2 = 0 . | (19) |
Taking into account that
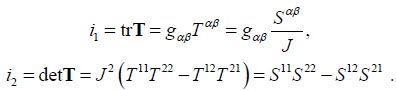 |
and considering that, in the case study a = 6.42m, b = 7.25m, h = 5.10m, h1 = h = 5.10m, h2 = 4.51m, by solving (19), we obtain, in Ω1
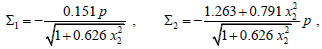 |
and in Ω2
 |
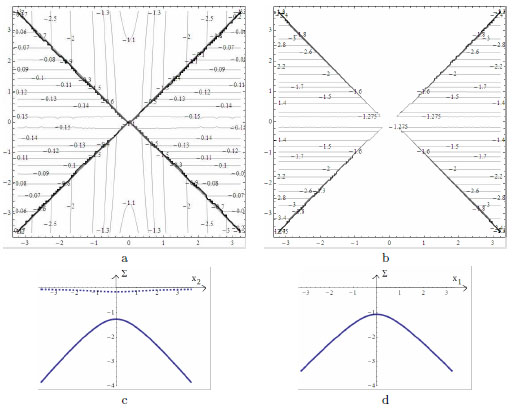
Notice that the previous formulas are dimensional, in the sense that the load per unit area p must be given in kNm-2, and Σ1, Σ2 read in kNm-1.
One way to obtain physical components is, instead, to consider a variable orthonormal system
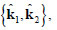 tangent to S, and obtain the Cartesian components T(αβ) of T in such reference system, through the formula
tangent to S, and obtain the Cartesian components T(αβ) of T in such reference system, through the formula
T(αβ) = T ∙ (k̂α
 k̂β) . k̂β) .
|
(20) |
Taking into account, again, that Tαβ = J-1Sαβ and recalling (2), from (20) one obtains
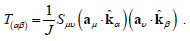 . .
|
By choosing, in Ω1:
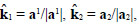 , and in Ω2:
, and in Ω2:
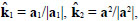 in the case study, one obtains, in Ω1
in the case study, one obtains, in Ω1
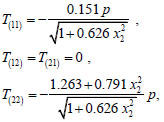 |
(21) |
and in Ω2
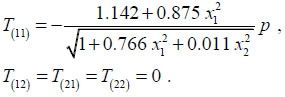 |
(22) |
From (21), (22) we deduce that the directions k̂1 , k̂2 chosen in Ω1, and Ω2, are eigenvectors for the surface stress in the regions Ω1, and Ω2 respectively.
Also these formulas are dimensional, in the sense that the load per unit area p must be given in kNm-2, and T(αβ) are generalized stress components which read in kNm-1.
The contour plots of these physical components are shown in Figs. (8a, b). In Figs. (8c, d), plots of the nonvanishing stress components at the boundary, are reported. Finally the axial force along the diagonal ribs
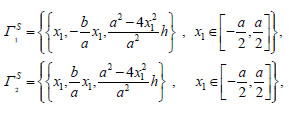 |
can be obtained by the contact axial force N. Taking into account that, in the case study, the unit tangent to the rib, say Γ1S , is:
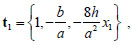 |
and that, recalling (18), the value of the projected axial force, in the case study, is:
| N = -1.688 |x1| p , | (23) |
one obtains:
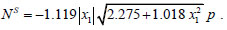 |
(24) |
In Fig. (7c), plots of the axial force NS and of its projection N, are reported. From (23), (24) the value of the axial force PS at a vertex and of its projection P can be calculated:
| P = −5.417 p , PS = −12.83 p . | (25) |
Notice that the formulas (23), (24), (25) are dimensional, in the sense that the load per unit area p must be given in kNm-2, and N , NS, P , PS, read in kN.
CONCLUSION
The present paper is concerned with an application of the safe theorem of Limit Analysis to the study of the equilibrium of a Gothic cross vault under the effect of pure vertical loading. The possibility of applying the theorems of Limit Analysis to masonry structures, stems from the adoption of the so called masonry-like model, that is essentially the model of Heyman describing Rigid No-Tension materials.
Based on the particular results that we present here, the cross vaults that we consider (the cross vaults of the transept of the Cathedral of Casertavecchia) are in a compressive, stable state of equilibrium and the stress level is small compared with the limit strength of the stones. Besides the distributed thrust transmitted to the walls and to the lateral arches, and the concentrated thrust transmitted to the piers, give rise to internal forces largely comprised within the thickness of the masonry.
The approach we propose is not restricted to the particular case that is considered, and can be applied to cross vaults of general shape, that is having different rises along the sides and at the center.
The method, put forward in by Angelillo, Fortunato in the paper [4], and applied to simple vaults by Angelillo et al in [1] and to spiral stairs by Angelillo in [2], leans on the use of singular stresses concentrated on surfaces (membranes), on the Monge representation through a function f of the membrane surface, and on the Pucher formulation of membrane equilibrium.
For parallel external loads, the Airy stress solution of equilibrium, based on a stress function F , can be adopted. In this case, the equilibrium of the vault is described by two scalar functions: the function f , representing the shape, and the function F , representing the stress. On assigning the shape f, the stress function F is determined by solving the second order differential equation of transverse equilibrium. Vice versa, if F is given, the shape f is found by solving the same equation. In both cases the problem is constrained, since F must be concave in order that the stress be compressive, and the surface described by f must be contained inside the masonry due to the No-Tension assumption.
In the present paper we adopt the second strategy, namely we assign a restricted class of stress functions F and find a function f that is contained within the masonry, by solving the equation of transverse equilibrium. In general the search of the couple (f, F ), can be formulated as an optimization problem, constrained by an equality constraint (the transverse equilibrium equation), and the inequality constraints resulting from the No-Tension assumption. The objective function to be minimized could be either the stress energy of the membrane or a scalar measure of the thrust of the vault. The development of this line of research, deserving further study, is encouraged by the preliminary results concerning cross vaults that we present here and in the recent papers [2, 3], where simple vaults and spiral stairs are considered.
CONFLICT OF INTEREST
The author confirms that this article content has no conflict of interest.
AKCNOWLEDGEMENTS
Decleared None.




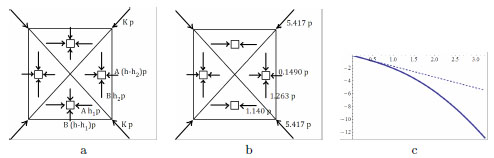
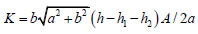 . In (b) schematic picture of the projected stress field corresponding to the stress function (17), in the case study; the load per unit area p must be given in kNm-2, and the projected stress components, are generalized stresses which read in kNm-1. In (c), plot of the projected axial force along the diagonals (dashed line) and of the axial force along the fold (solid line), as a function of x1, in the interval [−a/2, a/2].
. In (b) schematic picture of the projected stress field corresponding to the stress function (17), in the case study; the load per unit area p must be given in kNm-2, and the projected stress components, are generalized stresses which read in kNm-1. In (c), plot of the projected axial force along the diagonals (dashed line) and of the axial force along the fold (solid line), as a function of x1, in the interval [−a/2, a/2].