All published articles of this journal are available on ScienceDirect.
Structural Behavior of Layer-Printed Reinforced Concrete Beams
Abstract
Three-dimensional printing with atypical paste and mortar mixtures has been a topic of research and demonstration within the commercial and military sectors for several years. However, to the authors’ knowledge, printing with traditional concrete (a mixture of cement, fine- and coarse aggregate, and gravel) has yet to be investigated at the scale of habitation structures. This article explores the concrete material properties, printing process, and flexural testing of three-dimensionally printed concrete beams.
Objective:
The study aims to perform bending tests of nine normal strength, additively manufactured concrete beams when reinforced with various combinations and types of meshes and bars, and determine the flexural capacity of each reinforcement combination and type.
Methods:
The structural behavior of each layer-printed beam was evaluated in third-point loading to failure. All beams were printed to mimic a simply supported, flat roof beam spanning 4.57 m, incorporating seven varied reinforcement schemes.
Results:
Results show a layer-printed concrete beam with infill webbing that commonly fails in the shear span due to weak nodal connections. Test results also indicate that, in layered beam configurations, the interface between concrete and reinforcement significantly influences overall beam performance.
Conclusion:
Test results indicate that the interaction between concrete and reinforcement in layer-printed beams did not adequately bond for optimal beam performance. Further testing and variation the size, placement, roughness of beam reinforcement and thickness of concrete layers are needed to fully characterize the effect each reinforcement scheme has on flexural capacity and ductility
1. INTRODUCTION
Concrete Three-dimensional [3D] printing technology, developed by the authors and their co-performers, is centered on large-scale construction, utilizing computer-automated hardware to control spatial motions of printers while extruding planar, shape-stable concrete material in a continuous layering process. The concrete mixture and printer hardware must work systematically. The volumetric discharge of the concrete material must be consistent with the speed of the printer to enable continuous flow that may also stop, restart, and create steps for each new layer as needed. This type of 3D printing is a rapidly growing technology. However, while scale model research results using 3D printed forms are available [1], research on large-scale 3D printing with concrete materials is limited [2]. Current demonstration projects have been reviewed in a recent International Union of Laboratories and Experts in Construction Materials, Systems and Structures (RILEM) Technical Letter [3]. The reviewed projects tended to focus on atypical paste or mortar mixtures that contained little or no coarse aggregate. Despite numerous news articles reporting on advances in 3D printing, to the authors’ knowledge, this is the first peer-reviewed publication to report full-scale tests of reinforced concrete beams constructed by 3D printing. Since infill and reinforcement schemes remain under development, no attempts are made here to compare these printed concrete beams with conventional reinforced concrete beams.
The objective of this study was to determine the flexural capacity of printed beams with different reinforcement configurations under typical loading demands. While the design of reinforced concrete beams is a well-established field, layered concrete beams constructed with a 3D printer are relatively new. Layered beams are expected to behave differently from traditional concrete beams for the following three reasons: (1) interfacial bonding between layers can be limited, (2) reinforcement is constrained by the dimensions of the printer nozzle, and (3) traditional shear reinforcement using stirrups or studs is difficult or impossible to properly execute, as discussed by Wangler and co-authors [3].
2. MATERIALS AND METHODS
2.1. Test Specimens
Nine concrete beams were designed and printed to emulate typical roof components for military barracks huts (B-Huts). Of these nine, eight beams were reinforced and one was unreinforced. The reinforcements were placed by hand by pausing the printer between layer depositions. Typical B-Hut dimensions are 4.88 x 9.75 m, as described by the Army Facilities Components System (AFCS). The beams printed for this study were 4.88 m long and were tested as simply supported, unbraced roof components over a span of 4.57 m.
The printed concrete beams were tested in third-point bending. Eight beams had cross sections of 203 mm deep by 140 mm wide, and one beam had a cross section of 254 mm deep by 140 mm wide. All beams were 4.88 m long, with 4.57 m of clear span during the tests. All beams were printed as slender beams with a high shear span to depth ratio of 6 or greater. The beams were printed vertically, along the perpendicular direction to gravity, without formwork. Each beam had six printed layers, and each layer was approximately 35 mm thick.
The concrete mixture design used to print all beams in this study consisted of Type I cement, fine aggregate, coarse aggregate, and gravel at a ratio of 1:1.25:1.25:1, respectively. The mix design had a target water-to-cementitious (w/c) ratio of 0.47, although adjustments due to aggregate moisture conditions may have resulted in ratios from 0.45 to 0.52. A maximum coarse aggregate size of 9.5 mm was used since aggregates larger than 9.5 mm would not flow properly through the printing nozzle. To meet the required flowability, strength, and shape stability for printable concrete, dry additives (fly ash, silica fume, and bentonite clay) were included in the mixture. Fly ash improves the workability of concrete without impacting shrinkage [2]. On the other hand, silica fume stiffens fresh concrete workability while increasing the early-age strength through denser interfacial transition zones and bonding [4]. Bentonite enhances the bonding between layers and improves shape stability in self-consolidating concrete [5]. Liquid admixtures (plasticizer, rheology controller, and accelerator) were also used to achieve target strength development and rheological parameters. Batches were produced approximately 0.13 m3 at a time, so each beam required two to three batches of concrete, including waste.
Based on the infill configuration, the beam cross section is non-prismatic. This results in multiple cross-sectional configurations which vary beam material properties, such as the moment of inertia and stress assumptions at critical sections. Balduzzi and co-authors [6] discuss the difficulty of modeling shear stress distributions in non-prismatic beams. Here, the authors maintain a simplified analysis of moments of inertia for three basic beam sections. The three cross-sectional configurations shown in Fig. (1) were determined to be the most common and critical. These sections are specified by concrete strip size and void number.
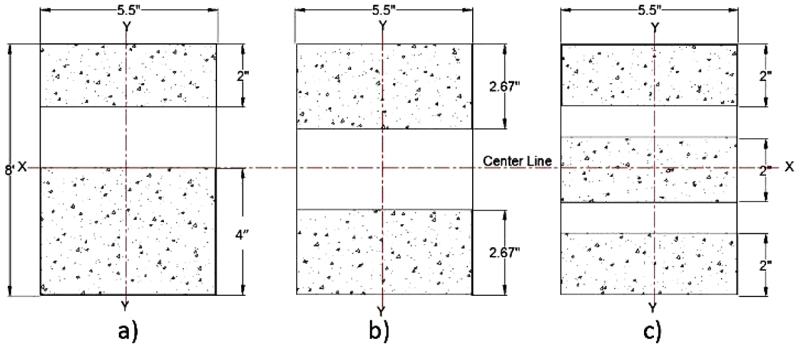
In order to compute the stress at the most critical section, the corresponding moment of inertia was first calculated by using the parallel axis theorem. For section a) in Fig. (1), (with depth of 203 mm), the centroid of the beam, as measured from the bottom is calculated by the following equation:
 |
(1) |
The moment of inertia about the x-axis for a depth of 203 mm is calculated as:
 |
(2) |
Similarly, for section a) with beam depth of 254 mm the centroid is calculated as:
 |
(3) |
And, the moment of inertia about the x-axis for a 254 mm depth is calculated as:
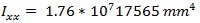 |
(4) |
The moment of inertia about the y-axis with a beam depth of 203 mm would be:
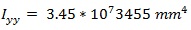 |
(5) |
And for a 254 mm beam depth, the moment of inertia about the y axis would be:
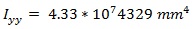 |
(6) |
The moments of inertia for sections in Fig. (1) are summarized in Table 1.
| Beam Width | Section a | Section b | Section c |
Solid Section |
||||
|---|---|---|---|---|---|---|---|---|
|
Ixx (mm4) |
Iyy (mm4) |
Ixx (mm4) |
Iyy (mm4) |
Ixx (mm4) |
Iyy (mm4) |
Ixx (mm4) |
Iyy (mm4) |
|
| 203 mm | 8991 | 3445 | 9407 | 3080 | 8699 | 3455 | 9781 | 4620 |
| 254 mm | 17565 | 4329 | 18356 | 3829 | 16982 | 4329 | 19063 | 5786 |
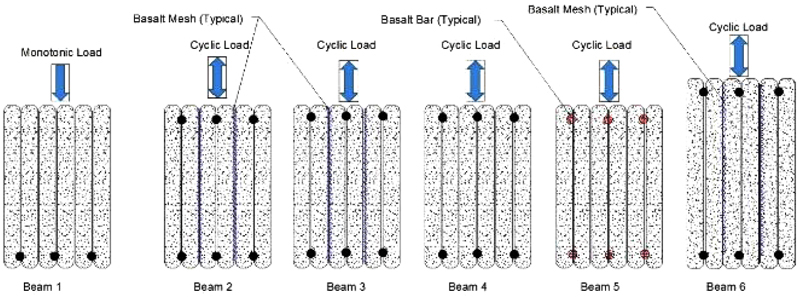
A variety of reinforcement configurations were used to determine the behavior of each reinforcement type, either individually or combined. All reinforcement configurations are listed in Table 2. Of the nine printed beams, six were reinforced with rebar, two were only reinforced with mesh, and one lacked reinforcement. Only one beam was singly reinforced with No. 3 deformed steel rebar. All other rebar-reinforced beams were doubly reinforced. One beam was doubly reinforced with No. 3 basalt rebar. One beam was reinforced with 25 mm basalt mesh. The remaining beams reinforced with mesh utilized 6 mm basalt mesh. The last three beams were damaged during preloading, so cut sections were loaded over a shorter span and the results were scaled up in order to compare results across all beams.
| Beam ID | Description | Depth (mm) | Clear Span (m) | Rebar | Basalt Mesh | Rebar Quantity and Type of Reinforcement |
|---|---|---|---|---|---|---|
| 1SR-S-0 | Singly reinforced | 203 | 4.57 | Standard | No | 3 - No. 3 Tension |
| 2DR-S-6B | Doubly reinforced | 203 | 4.57 | Standard | 6 mm Basalt | 3 - No. 3 Tension 3 - No. 3 Compression |
| 3DR-S-6B | Doubly reinforced | 203 | 4.57 | Standard | 6 mm Basalt | 3 - No. 3 Tension 3 - No. 3 Compression |
| 4DR-S-0 | Doubly reinforced | 203 | 4.57 | Standard | No | 3 - No. 3 Tension 3 - No. 3 Compression |
| 5DR-B-0 | Doubly reinforced | 203 | 4.57 | Basalt | No | 3 - No. 3 Tension 3 - No. 3 Compression |
| 6DR-S-6B | Doubly reinforced | 254 | 4.57 | Standard | 6 mm Basalt | 3 - No. 3 Tension 3 - No. 3 Compression |
| 7UR-0-0 | Plain concrete | 203 | 4.57* | None | No | None |
| 8UR-0-6B | Mesh only | 203 | 4.57* | None | 6 mm Basalt | None |
| 9UR-0-25B | Mesh only | 203 | 4.57* | None | 25 mm Basalt | None |
It should be noted that, while the use of No. 3 rebar conformed to American Concrete Institute (ACI) specifications of reinforcement ratio, two key issues stem from the relative area of reinforcement in the overall cross section. First, the voids in sections drawn in Fig. (1) will effectively reduce the depth parameter and increase the reinforcement ratio, perhaps over the maximum specification. Additionally, and perhaps more importantly, the relatively small area of concrete engaging the reinforcement will increase the developmental length of load transfer to the reinforcement. If load transfer does not fully develop, the concrete will slip and crack before the reinforcement yields, effectively reducing the yield strength of the tensile section and the overall strength of the entire beam. Future investigations should either source deformed No. 2 rebar or increase the amount of concrete in contact with rebar to enhance load transfer near and after stress failure.
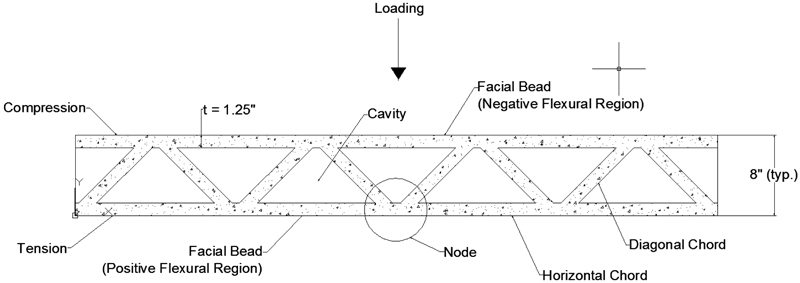
Beams were printed with the cross-sectional details shown in Fig. (2). The longitudinal cross section of the printed beams is shown in Fig. (3). Each beam layer was printed with a facial bead to define the perimeter and then filled with a sinusoidal, “zig-zag” bead. The bead thickness and reinforcement sizes were limited by the nozzle dimensions.
2.2. Test Setup
Each beam was tested as a simply supported beam under third-point bending. A schematic of the third-point bending laboratory test setup is shown in Figs. (4 and 5). Each beam was laid on its side over friction-reducing plastic panels and loaded horizontally, along the vertical axis. Friction forces inherent to the loading frame were removed from the data during analysis. An actuator, supported by a reaction wall, applied a single load to a structural steel tube fabricated specifically for the horizontal test setup. The actuator load was transmitted through the steel tube into two point loads on the beam using steel half-cylinder rollers.
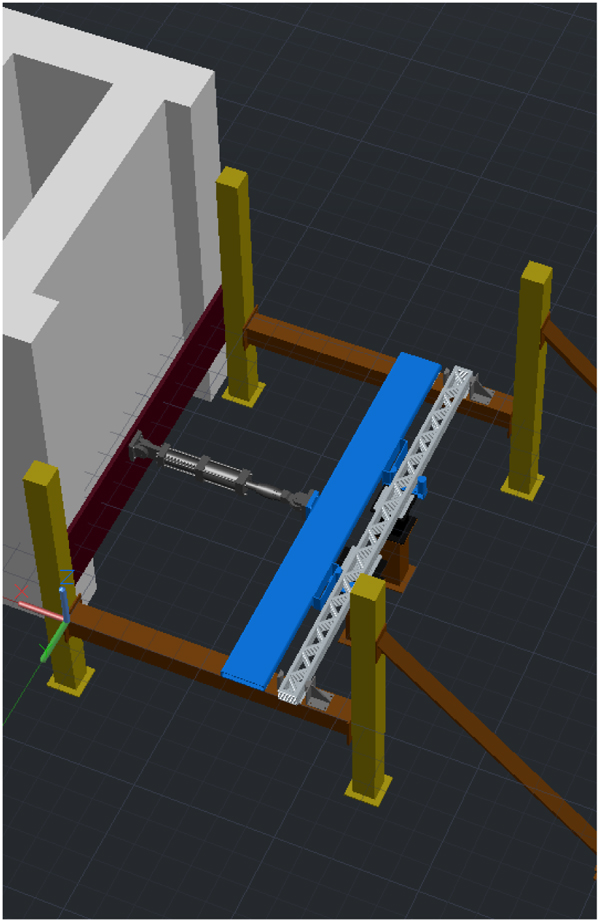
The third-point load test was used since the flexural strength of a beam is a key design factor for roof components. Under an ideal third-point load test, the shear between the point loads (center span) is zero, and the beam is expected to fail near the center under a pure moment. Despite the efforts to avoid mixed-mode failures in this test setup, the beam may experience shear failure in the end spans.
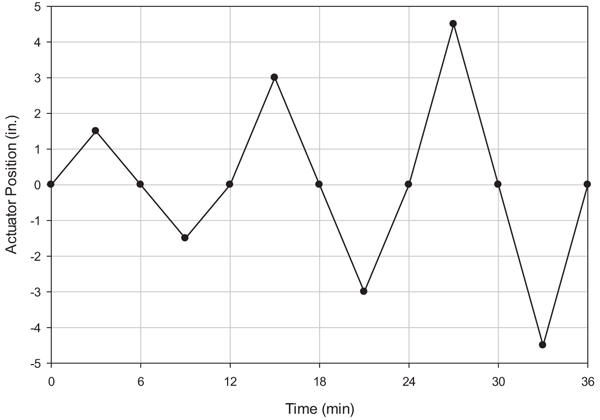
Cyclic third-point bending tests were performed for doubly reinforced beams. Supports and point loads were positioned on the top and bottom of each beam for cyclic tests. Beam displacement at the center, beam displacement at the loading points, and actuator load and displacement were continuously recorded at 250 kHz and reduced to 1 kHz in post-processing. Each test was displacement-controlled with 3 cycles of varying maximum displacement and displacement rate. The first cycle began by pulling the beam toward the reaction wall (positive y-direction) until an actuator displacement of 38 mm from the origin was reached. Then, the beam was pushed away from the reaction wall (negative y-direction) until an actuator displacement of 38 mm in the opposite direction was reached. The cycle finished when the beam was pulled back to the origin. The second and third cycles repeated the same process as the first, except with maximum actuator displacements of 76 mm and 114 mm. Each cycle took 12 minutes from start to finish, so the displacement rate for the first, second, and third cycles was 13 mm/min, 25 mm/min, and 38 mm/min, respectively. Fig. (6) depicts the displacement pattern and time to completion. All beams underwent this cyclic pattern except the singly reinforced beam, which only experienced positive beam displacement to place the reinforcement in tension. The beams lacking rebar were fragile and failed under self-weight during test setup. Therefore, saw-cut sections 2.44 m in length were tested using a smaller, vertical load frame. The maximum applied load and beam displacement were recorded, and the equivalent loads and displacements for beams 4.57 m in length were determined analytically.

3. RESULTS
Table 3 provides a summary of the residual load at maximum displacement and the maximum stress experienced by each beam.
| Beam | Residual Load at Absolute Maximum Displacement | Load at Absolute Maximum Stress | ||||
|---|---|---|---|---|---|---|
| Displacement (mm) |
Load (N) |
Stress (kPa) | Displacement (mm) | Load (N) | Stress (kPa) | |
| 1SR-S-0 | — | — | — | 51.3 | 12811 | 11714 |
| 2DR-S-6B | 73.4 | 10191 | 9315 | 53.6 | 17673 | 16154 |
| 3DR-S-6B | 74.4 | 5667 | 5178 | 60.5 | 18207 | 16644 |
| 4DR-S-0 | 74.4 | 10026 | 9163 | 31.8 | 14154 | 12935 |
| 5DR-B-0 | 77.5 | 4422 | 4040 | 58.4 | 7958 | 7274 |
| 6DR-S-6B | 75.4 | 8412 | 4792 | 32 | 16619 | 9473 |
| 7UR-0-0 | — | — | — | 2.79 | 3612 | 3213 |
| 8UR-0-6B | 7.41 | 267 | 234 | 1.52 | 4288 | 3820 |
| 9UR-0-25B | 22.6 | 1121 | 1000 | 17.5 | 1957 | 1737 |
A brief description of beam behavior and failure mode follows here, along with plots of hysteresis curves. Reported displacements and stresses are the absolute maximum; beams may have achieved these stresses in either the positive or negative direction. The corresponding moments and stresses at the surface of the beam in critical section c) in Fig. (1) were calculated from the measured values according to classical beam theory, as follows:
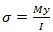 |
(7) |
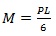 |
(8) |
Therefore,
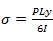 |
(9) |
where y is the centroid of the beam for critical cross-section c) in Fig. (1) and Table 1 is the moment of inertia for critical section c), L is the clear span of the beam, and P is the maximum load from Table 3. A sample calculation of moment and stress from Beam 1SR-S-0 would be:
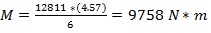 |
(10) |
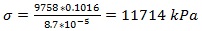 |
(11) |
As stated previously, the beams lacking rebar were cut into sections 2.44 m long and tested with a smaller, vertical load frame over a 1422 mm span. Given that both the short and long beams were tested in third-point bending, determining an equivalent critical long beam applied load followed by an analysis of moments applied to each, would be calculated in the order of equations below:
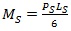 |
(12) |
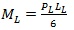 |
(13) |
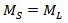 |
(14) |
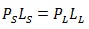 |
(15) |
Therefore,
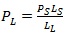 |
(16) |
where PL and PS are the loads applied to the long and short beams, respectively, and LL and LS are 4.57 m and 1422 mm, respectively. As stated above, the equivalent loads and stresses are shown in Table 3. Displacements were measured by a Linear Variable Differential Transformer (LVDT) at the center of the short beams.
3.1. Beam 1SR-S-0, Singly Reinforced with Steel
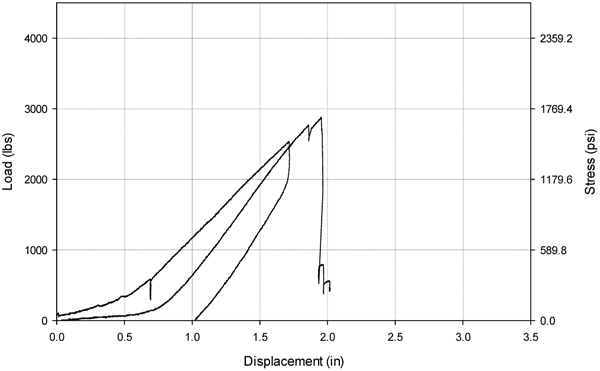
Beam 1SR-S-0 was singly reinforced with three No. 3 steel rebar placed in the positive flexural region. Since there was no reinforcement in the negative flexural region, the beam was only loaded in one direction. The stress-displacement response is shown in Fig. (7). Beam 1SR-S-0 completed the first cycle (38 mm displacement), but the beam failed during the second cycle (76 mm displacement). It reached an absolute maximum displacement of 51.3 mm and an absolute maximum stress of 11714 kPa (12811 N). The maximum displacement was approximately 1/90 of the clear span, exceeding the allowable maximum midspan deflection by 25.4 mm. Heavy cracking near one side of the support was observed. The failure occurred in shear due to several diagonal chords splitting from the horizontal chords at the nodes. This shear failure is illustrated in Fig. (8).

3.2. Beam 2DR-S-6B and Beam 3DR-S-6B, Doubly Reinforced with Steel and 6 mm Basalt Mesh
Beams 2DR-S-6B and 3DR-S-6B were identical, doubly reinforced beams with three No. 3 steel rebar placed in the negative and positive flexural regions. The rebar was standard steel and was hooked on one end to anchor into the full depth of the beam. Basalt mesh was placed between each layer during printing. The mesh covered the entire beam, including the voids. Both reinforcement types were used to determine the load capacity and ductility of the reinforcement combination.
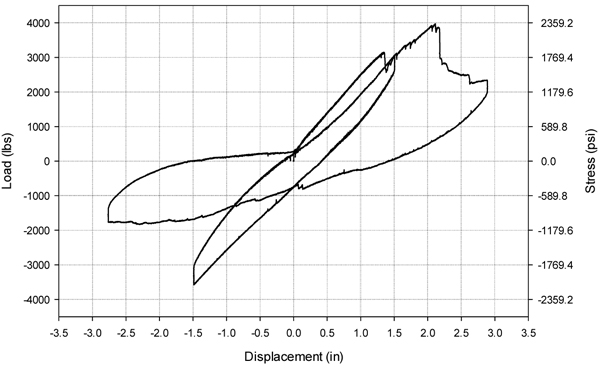
The stress-displacement responses are shown in Figs. (9 and 10). Both beams failed near the end of the second cycle, at 76 mm displacement. Beam 2DR-S-6B reached an absolute maximum displacement of 73.4 mm and an absolute maximum stress of 16154 kPa. Beam 3DR-S-6B reached an absolute maximum displacement of 74.4 mm and an absolute maximum stress of 16644 kPa.
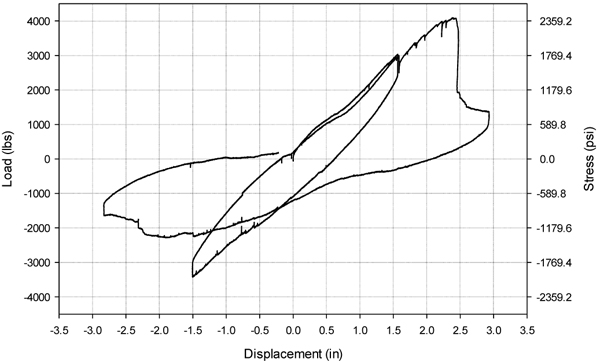
Several small cracks were observed along the outer spans near the point loads. The failure occurred in shear due to nodal fracture, similar to Beam 1SR-S-0. While the rebar and basalt mesh remained intact, structural integrity of the beam was lost due to the nodal failures. This was apparent in the third cycle (114 mm displacement), when the beam did not carry a significant load. In addition, bonding between concrete layers was shown to be weak in several places Fig. (11), but this weakness did not negatively impact structural integrity.

3.3. Beam 4DR-S-0, Doubly Reinforced with Steel
Beam 4DR-S-0 was doubly reinforced with three No. 3 steel rebar placed in the positive and negative flexural regions. Mesh was not placed in this beam configuration. The stress-displacement response is shown in Fig. (12). Beam 4DR-S-0 reached an absolute maximum displacement of 74.4 mm and an absolute maximum stress of 12935 kPa (14154 N). Only steel rebar was used in Beam 4DR-S-0 in order to determine the overall contribution of the steel to the performance and ductility of beams, unlike 2DR-S-6B and 3DR-S-6B that incorporated the second reinforcement of mesh.
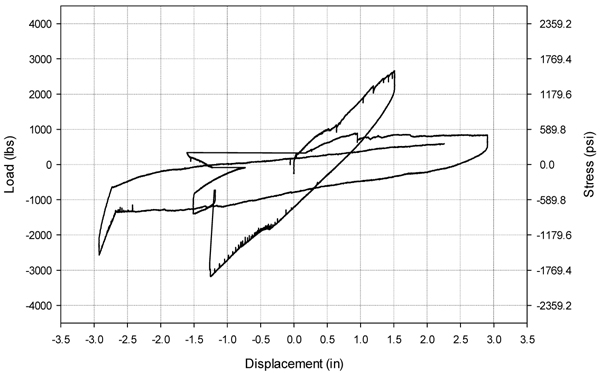
A small amount of cracking occurred in the sinusoidal beads before failure. The failure occurred after the peak of the second cycle. Testing continued after failure, since the beam was still able to hold load (4448 N in both flexural regions). Significant cracking was observed in the center and outer span nodes after failure occurred. Similar to Beam 2DR-S-6B and 3DR-S-6B, failure was observed near the supports. There was a complete detachment of the nodes from the facial chords. The spalling and failure behavior of the beam is shown in Fig. (13).

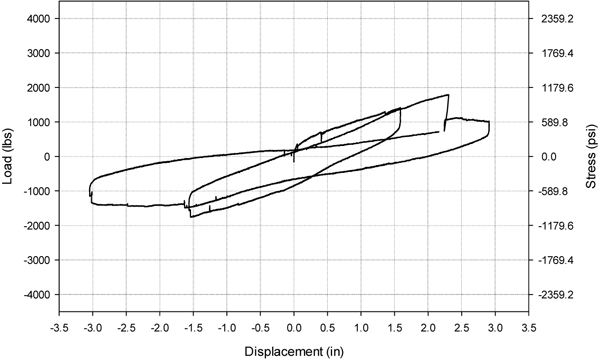
3.4. Beam 5DR-B-0, Doubly Reinforced with Basalt
Beam 5DR-B-0 was doubly reinforced with three No. 3 basalt rebar placed in the positive and negative flexural regions. Mesh was not placed in this beam configuration. Beam 5DR-B-0 reached an absolute maximum displacement of 77.5 mm and an absolute maximum stress of 7274 kPa (7958 N). The stress-displacement response is shown in Fig. (14).
Failure occurred from the detachment of the rebar from the concrete, after which the beam was unable to carry a significant load (Fig. 15). Since the basalt rebar was delivered in a roll, residual curvature contributed to the material’s poor bond with the concrete. Shear failure due to nodal fracture also occurred in the outer spans.

3.5. Beam 6DR-S-6B, doubly reinforced with steel and 6 mm basalt mesh
Beam 6DR-S-6B was doubly reinforced with three No. 3 steel rebar, placed in the positive and negative flexural regions. Basalt mesh was placed between each layer during printing. This beam 6DR-S-6B was 254 mm deep instead of 203 mm. The stress-displacement response is shown in Fig. (16).
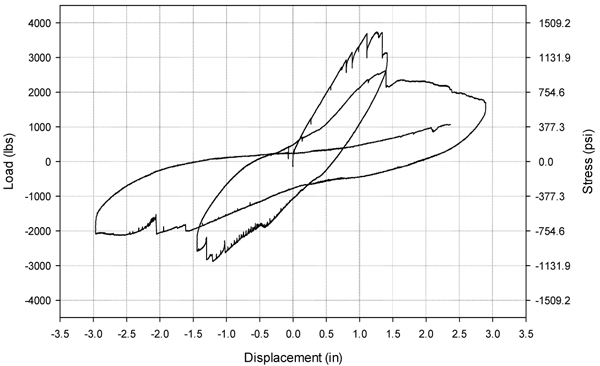
Beam 6DR-S-6B reached a maximum stress of 9473 kPa, (16619 N) in the first cycle. Several small cracks formed before the maximum value was reached due to the basalt mesh breaking. The mesh continued to tear through the end of the first cycle and into the second. The load capacity of the beam was decreased as the test continued. Failure occurred due to the breaking mesh, debonding of rebar, and shear failure at nodes Fig. (17). By the third cycle, only minimal load was carried. The maximum displacement reached was 75.4 mm.

3.6. Beam 7UR-0-0, lacking reinforcement and mesh
Beam 7UR-0-0 was considered the baseline beam. Reinforcement was not used, and the beam was loaded monotonically under a quasi-static third-point bend test. The beam had an initial printed length of 4.57 m, but it was not tested at this length since the beam damaged during preloading. Therefore, a section 2.44 m in length was cut out and tested on a vertical load frame over a 1.42 m span. The results were then analytically transformed to determine the equivalent load on a beam 4.57 m in length.
Beam 7UR-0-0 completed only one cycle, with a maximum displacement of 2.79 mm and stress of 2834 kPa (Fig. 18). The beam response was similar to an unreinforced cast concrete beam. The failure was dominated by flexural behavior, with one or two main flexural cracks forming at the center of the bottom of the beam (tension side) before immediately penetrating upward to the top of the beam.
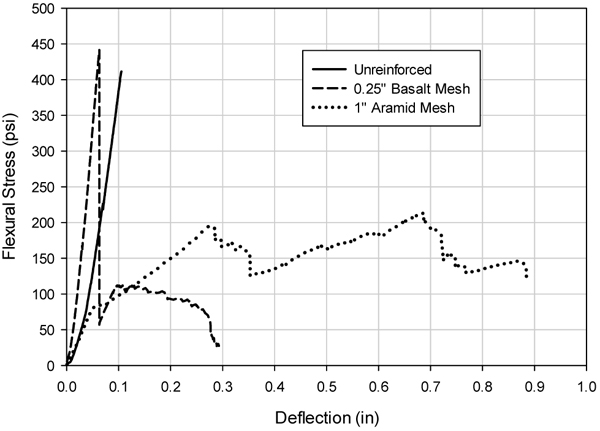
3.7. Beam 8UR-0-6B and 9UR-0-25B, Unreinforced, with Either 6 mm or 25 mm Basalt Mesh
Beam 8UR-0-6B was reinforced only with 6 mm basalt mesh, and Beam 9UR-0-25B was reinforced only with 25 mm basalt mesh. The mesh was placed between each layer during printing. As with the unreinforced beam 7UR-0-0, these beams were damaged during preloading, so sections were cut and loaded monotonically in third-point bending over a 1.42 m span.
Beam 8UR-0-6B reached a maximum displacement of 7.37 mm and a stress of 3047 kPa (fig. 18). The basalt mesh altered the beam’s behavior in two ways: increasing the capacity about 8% and resistance to brittle failure exhibited by an extended, nonlinear failure after maximum stress occurred. Failure occurred by flexural cracks at the middle of the bottom of the beam (tension side) and splitting of the basalt mesh.
Beam 9UR-0-25B reached a maximum displacement of 22.61 mm and stress of 1469 kPa (fig. 18). The 25 mm basalt mesh resulted in a nonlinear region three times longer than the 6 mm basalt mesh. However, significant strength reduction was observed due to poor bonding between the 25 mm basalt and concrete. Similar to Beam 8UR-0-6B, failure occurred by flexural cracks at the middle of the bottom of the beam (tension side) and splitting of the basalt mesh.
4. DISCUSSION
Modes of failure appeared similar for all beams in this test. Cracks and spalling began to show within the first cycle of the test, then a hinge effect developed at the loading points after beams achieved their maximum load due to a degree of freedom in the load frame. Interlayer bonding seemed strong, as cracking between layers was only observed adjacent to reinforcements. The most significant failure occurred in the nodes because the shear forces applied in the outer spans resulted in tensile and shear loads at the unreinforced nodes. The concrete was very weak in this region, and since there was no reinforcement to fully support tension or shear in these nodal zones, the horizontal chords detached from the diagonal chords. The horizontal chords were reinforced in most cases, so it was clear that the steel or basalt rebar aided in resisting tensile loads in these chords.
The reinforcement system will require significant improvement to produce a layer-printed beam capable of up to 114 mm of deflection. These improvements would include addressing the total area of reinforcement, increasing the relative area of concrete engaging the reinforcement, ensuring that the flexural reinforcement has deformed surfaces, and adding shear reinforcement at the nodes. Steel and basalt No. 3 reinforcement debonded from the small amount of concrete surrounding the rebar. Therefore, it is recommended that similar tests use No. 2 reinforcement with a rough surface to improve bonding between the rebar and concrete and to reduce the developmental length of the reinforcement.
Compared with Beam 4DR-S-0, the flexural capacity of Beam 5DR-B-0 decreased about 44%. The loss of performance was likely not caused by the material properties of the basalt rebar; rather, the smooth basalt rebar surface did not enable effective load transfer to the reinforcement. On the other hand, when comparing beams 2DR-S-6B and 3DR-S-6B with beam 4DR-S-0, the data show that 6 mm basalt mesh increased the maximum load capacity of the beam by about 27% and the displacement at maximum stress by at least 60%. The residual load at large displacements was not significantly affected. Basalt mesh imparted a nonlinear, semi-ductile behavior without compromising strength capacity.
Finally, the effects of beam depth can be compared with the quantity of reinforcement. Beam 6DR-S-6B was 50.8 mm deeper than beams 2DR-S-6B and 3DR-S-6B, but 6DR-S-6B failed at both lower load and stress after considering the change in moment of inertia and centroid. The singly reinforced beam 1SR-S-0 failed in a nearly brittle manner, while doubly reinforced beams exhibited both significant ductility during failure and adequate residual load-carrying capacity. When lacking flexural reinforcement, 4.57 m long beams could not carry self-weight. These results are testaments to the necessity and effectiveness of either steel or basalt reinforcement in layer-printed beams. However, considering the results of beams 6DR-S-6B (deep) and 1SR-S-0 (singly reinforced), and the shear failure behavior at chord nodes, several opportunities exist to improve upon the reinforcement system tested here.
CONCLUSION
We briefly described the concrete mixture and its material properties, described the beam printing process and test setup, and provided testing results comparing the strength and ductility benefits and burdens of each reinforcement scheme tested. Most beams failed at nodal connections between diagonal and horizontal chords. Double reinforced beams exhibited significantly higher strength and residual load-carrying capacity at larger deflections than singly reinforced beams. Smooth basalt rebar was not as effective as standard steel rebar when used for flexural reinforcement. While basalt mesh increased beam strength and ductility, it did not improve the post-peak load-carrying capacity. Furthermore, increasing beam depth to 254 mm reduced the beam load-carrying capacity compared with a similarly reinforced, 203 mm depth beam.
Further investigation into shear reinforcement at critical nodes to evaluate potential reduction in nodal failures and improvement in beam performance is recommended. Beam performance could also be improved by increasing the area of concrete engaging the reinforcement to reduce concrete spalling and layer debonding, and by using deformed-surface rebar to reduce the developmental length of load transfer to the reinforcement. Further testing, varying the size and roughness of steel rebar to fully characterize performance effects, is recommended.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors would like to acknowledge Tanner Wood and Hassan Issa for their contributions during the fabrication of the test setup. The authors also appreciate Hassan Issa for his efforts during the initial data collection and analysis. The program manager of the ACES program, Dr. Michael Case is also acknowledged.


