Energy Dissipation in Frame Structures using Sliding Lever Mechanism Technique

1. INTRODUCTION

Engineers have been struggling to evade the damaging effect of vibrations caused by various mechanisms. Over the past several years, researchers and engineers from the field of earthquake engineering have been collaborating to devise a mechanism that will efficiently dissipate the energy transmitted to the structures through various natural or man-made pheno- mena. The two main techniques used in this regard are to either allow a certain degree of damage in the structure or to have supplemental energy dissipating devices. In order to avoid damage to the structural components during seismic shaking, different types of passive energy dissipation techniques have been studied. The main function of these devices is to channel the detrimental drifts and energies from the main structure to one of these devices, where energy is ultimately lost in the form of heat energy [1, 2]. In the absence of such devices, the input energy will be transferred to load-bearing systems (beams and columns), causing excessive non-linear displacements which might be detrimental for the sanctity of structure [3, 4]. Various seismic energy dissipating mechanisms are used in the civil engineering industry, such as friction type [1, 2], viscous [5, 6], visco-elastic [7, 8] and metallic type dampers [9-11]. Different experimental and analytical studies have been conducted in the literature to verify the effectiveness, suitability and structural configuration of these passive control systems [12-28]. Shake table studies conducted by Bogdano- vic et al. [29] on a five-story reference steel model in order to investigate newly developed prestressed viscous dampers showed promising results. The sequence of increasing input acceleration records was used to excite the bare frame specimen with and without the damper devices in different configurations. From experimental studies, 70% decrease in the displacement response, 68% decrease in the acceleration response and about 6 times more energy dissipation were exhibited due to the provision of new Prestressed Viscous Dampers PVDs as compared to the bare frame test model. Bagheri et al. [30] conducted shake table tests on three-story and two bays braced steel structures with and without hysteric dampers. Two types of the test specimen, i.e. steel framing with concentrically braced system and another with steel framing with hysteric dampers, were considered during the experimental phase. The proposed hysteric damping devices were supplemented with increased stiffness, controlled hysteric behavior characteristics and provided with the specified yield strength along with the story height. It was confirmed from the experimental studies that 40% acceleration and 60% displacement response reduction were observed during the maximum shaking level. In order to investigate and optimize different types of metallic energy dissipation devices, Jaisee et al. [31] conducted shake table tests on a two-story steel frame structure. The test frame consists of two bays of length 5.25 feet (1600 mm) and story height of 9.32 feet (2840 mm) with two pair of metallic dampers installed on each story. The test frame with and without dampers was excited with an increasing level of excitations in order to compare different dynamic characteristics. It was revealed from the test results that the inter-story drift significantly reduced with increasing level of excitations with estimated drift angle within a range of 1/205. The majority of these studies focused on the brace-type damper devices and revealed the outstanding performance of such interventions in reducing the seismic demand on the structure. However, the typical braced configuration which is directly connected to the connection regions may attract more load demands on the structural column and beam members during extreme excitations [32]. Different braced configurations like diagonal, toggle and chevron showed good energy dissipation behavior, which may require the strengthening of the connected members in order to transfer the damping forces [33]. Sigaher et al. (2003) [33] studied a unique configuration of dampers, where the horizontal movement of the steel frame was amplified using a novel technique, the Scissor-Jack Energy dissipating system. The results of this testing showed promising results in terms of reduction in drift and accelerations. A comparison of various damping systems was presented in this paper and reproduced in Fig. (1) for reference. It can be easily verified that diagonal bracing will have 80% of horizontal displacement when the angle of the bracing system is 37^o and corresponding damping is 3%. With the same structural properties but a different damper configuration (chevron bracing), displacement amplification is 1 and the damping ratio of the system is 5%. This study aimed to develop another technique. To understand the working principle of this system, we recognize that the ratio of horizontal displacement at the story level to the damper displacement is smaller than one (in case of diagonal bracing) or equal to 1 (in case of chevron brace); mathematically, we can write as Eq. (1) [33]:

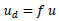(1)

Where is the displacement amplification factor; similarly the Damper Forces and net horizontal forces can be written as Eq. (2):

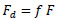(2)

The linear viscous dampers can have forces along their axis, which are given in Eq. (3):

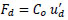(3)

Where is coefficient of damping and is relative velocity between the ends of dampers.

Therefore, the damping ratio in the system can be given as Eq. (4):

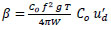(4)

Assuming a 5% damping in chevron bracing system, the corresponding damping will be 3% for the same damper when used in a diagonal configuration, and for scissor-jack, it will be 23%, as shown in Fig. (1). The sliding lever mechanism increases the damping from 5% to 7%. Such damping devices are required where the inter-story drift is significantly smaller and requires special attention to the detailing and designing of dampers, which will increase the cost of dampers.

The amplification factor for this geometric configuration is given by Eq. (5):

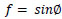(5)

Where Ø is the angle of the lever horizontally.

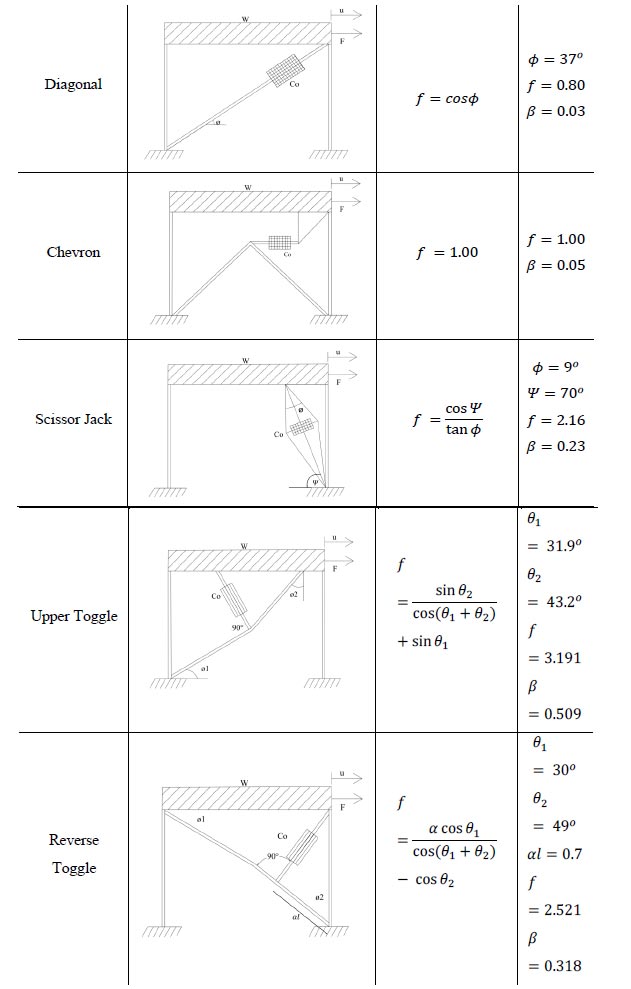
To validate the concept of sliding lever mechanism, dynamic testing was performed on the steel moment frame structure. The developed new mechanism would not increase axial or shear demand on columns, which is the main problem with the conventional energy dissipation bracing devices. A reduced scale, three-story and one bay in each direction steel frame model was dynamically tested on a shake table for Imperial Valley 1979 Earthquake records with and without the new configuration. The geometric configuration of the supplemental damping was designed such that it did not alter the shear and axial demand on columns.

2. SLIDING LEVER MECHANISM TECHNIQUE

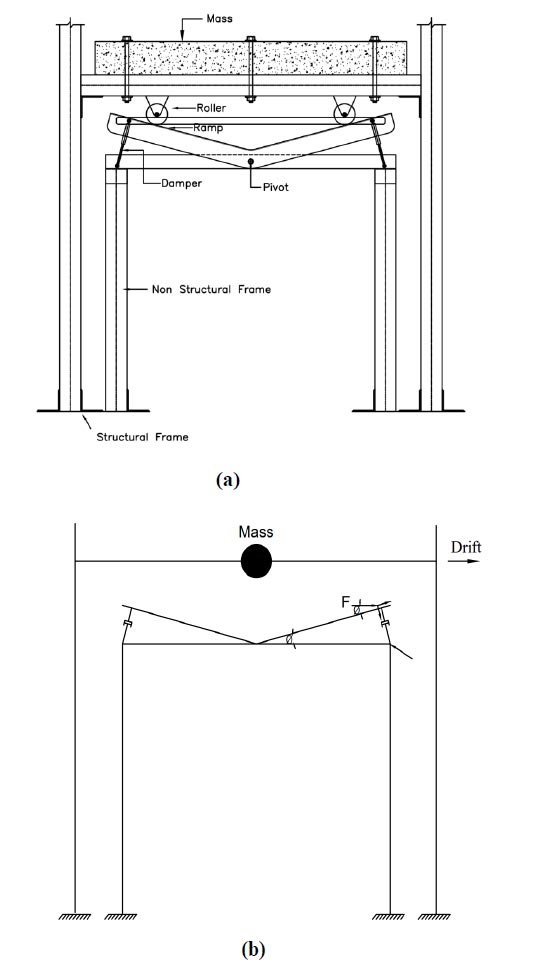
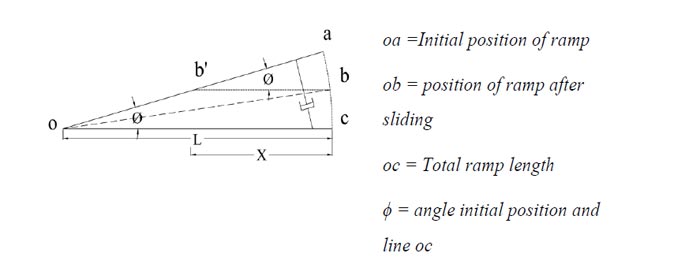
Most of the available energy dissipation damper configu- rations require to install and connect the braces and dampers directly to the structural members, i.e. beams, columns and their connection regions. Such configuration can cause extra loading demand on these structural members, and sometimes, the proposed energy dissipation scheme for existing structures may require also the strengthening and retrofitting of structural members [24]. In the currently proposed sliding lever energy dissipation configuration, the force transfer from dampers is resisted by a non-structural frame member and the energy is dissipated by a sliding lever mechanism provided through a ramp and damper assembly installed on the non-structural frame, as shown in Fig (2). As can be seen from Fig. (2), the transfer of structural displacement to the non-structural frame is supported by the ramp and damper assembly. When the structure deflects on one side, due to the connected rollers on ramp-damper assembly, the same side of the assembly acti- vates the damper. Due to the lever mechanism, the other side of the ramp will be forced to move upward and that will cause to activate the second damper on the opposite side. This will also cause two dampers to dissipate energy simultaneously. The total vertical displace- ment drop can be calculated using Fig (2) and Fig (3), and is the basis for Eq. (4).

3. EXPERIMENTAL PROGRAM

3.1. Description and Geometry of Structure

In order to investigate the effectiveness of the proposed sliding lever energy dissipation technique through the shake table test, a regular three-story steel frame with a tube section (for beam and column members) was considered. Due to the limitation of the shaking simulator, a one-third scaled reduced test model was developed and fabricated for testing purposes. Fig. (4) shows the schematic view and geometry of the experimental model, which consists of three-story and one bay frame in each direction. For the reduced scale model, a one third scaled height of 1219.2mm (4 feet) and a bay length of 1295.4mm (4.25 feet) and 990.6mm (3.25feet) in x-direction and y-direction respectively, have been considered for the testing purpose.

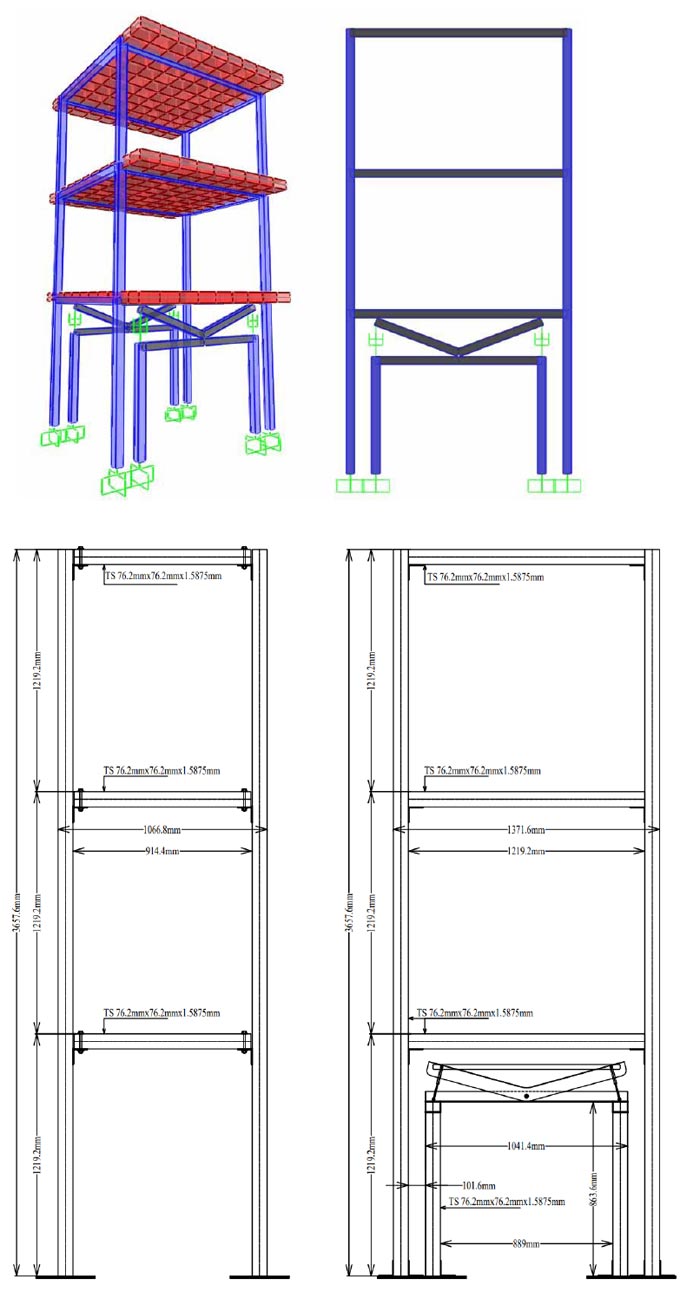
The selection of a regular framing system was based on the limitation of the shaking simulator table size and the choice of three-story was to compare the undamped as-built model with the damped (sliding lever dissipation technique installed model) in the required range of drift and acceleration limits. For the analysis and the design of the prototype frame model, SAP2000 analysis platform has been unitized, using different trial sections for the beam and column members. After a number of dynamics analyses using different natural acceleration records, e.g. EL Centro 1940, Northridge 1994, Imperial Valley 1979 and Kashmir 2005 acceleration records and based on the practical availability of reduced size steel section, a 76.2mm x 76.2mm (3in x 3in) tube section with a thickness of 1.59mm (1/16in) was considered for both beam and column sections.

3.2. Structural and Non-Structural Frame

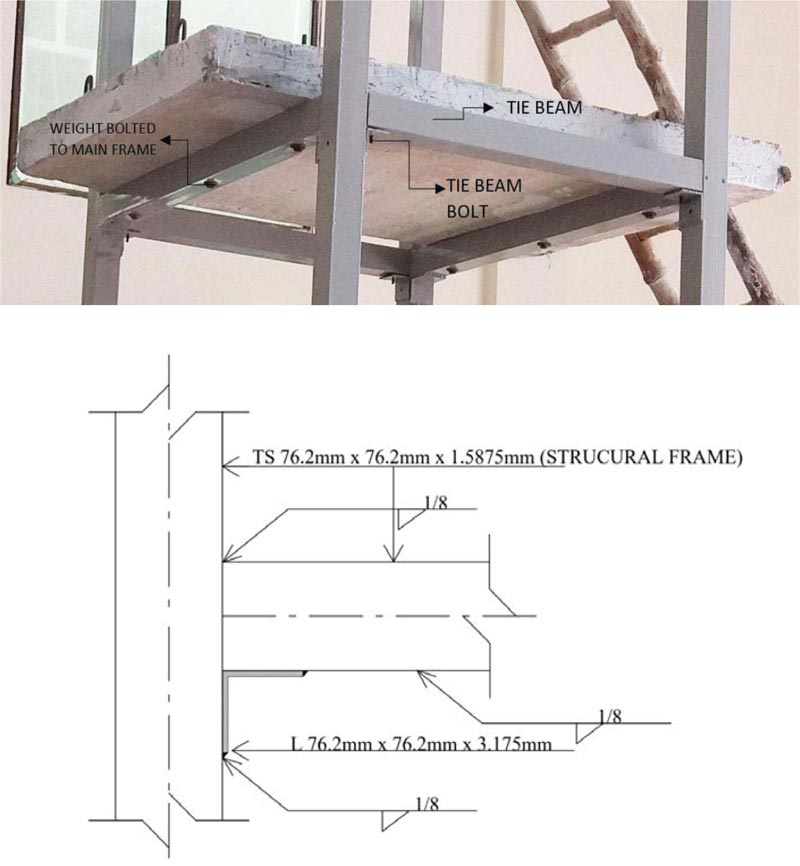
In order to install the proposed damping dissipation technique, the test model has been divided into two components. A structural main frame, which is the outer load carrying frame, and a non-structural inner frame, which does not carry any gravity load and lateral loading, but is provided to install sliding lever energy dissipation technique and connected to the main structural frame through the roller support. The main purpose of providing the non-structural frame is to install the ramp and the damper assembly on two columns with fixed support conditions. The arrangement of the non-structural frame and the sliding lever mechanism is shown in Fig (4). Two non-structural frames are provided in plane and between the two bays of outer structural frame in the x-direction only. For the non-structural frame, the same tube section of 76.2mm x 76.2mm (3in x 3in) and 1.59mm (1/16in) thickness is considered, whereas the height and bay length are based on the arrangement of sliding lever ramp-beam arrangement. The offset distance between the columns of the structural and non-structural frame is based on the allowable maximum drift limits based on time history analysis using acceleration records.

Initially, the columns of both structural and non-structural frame are welded to steel plate with predefine holes, through which the test model is fixed on the shake tabletop. After that, the structural frame columns are welded and connected to beam members, using a common L-shape 76.2mm x 76.2mm (3in x 3in) and 3.175mm (1/8in) section. Fig. (5) shows the test model fabrication sequence. The design of the structural frame's fixed connections was made mainly using the simulation results of the time history analysis. For the non-structural frame, the same column section was used, whereas, in order to provide the assembly for the dampers and ramp beam, an inverted steel C channel section with 76.2mm x 76.2mm (3in x 3in) and 1.59mm (1/16in) thickness has been used as a beam, as shown in Fig. (6). The inner faces of the non-structural beam and ramp C sections were towards each other so that to provide a type of casing for the damper assembly. For this purpose, the ramp steel C section's width was about 12.7mm (0.5in) wider than the beam section, so that damping and deformation actions could take place without any friction or obstructions. As the non-structural frame does not support the gravity load, the structural and non-structural frame will vibrate with different time periods and frequencies. The ramp section was pivoted at the midpoint of the non-structural beam section so as to provide a see-saw action, i.e. when one end of the ramp is trying to compress, the other end will rise up. In order to provide stiffness to the ramp-beam and damper assembly, a steel strip of 1.59mm (1/16in) thickness was tied between the two ends of the ramp beam.

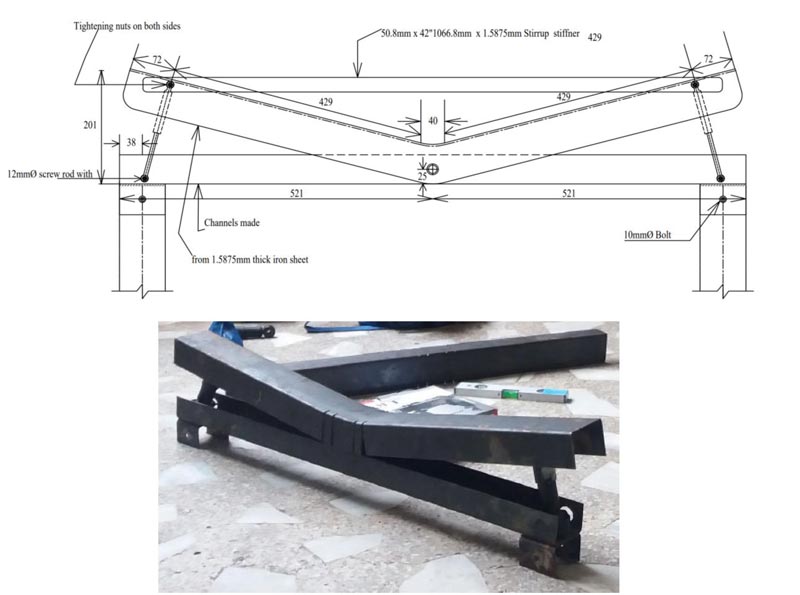
The slope angle of the ramp and the type of dampers are the two important parameters which affect the overall damping and energy dissipation mechanism. In the current study, the slope angle of the ramp was based on the available small size dampers in the local market, which has been utilized in the current dynamic testing.

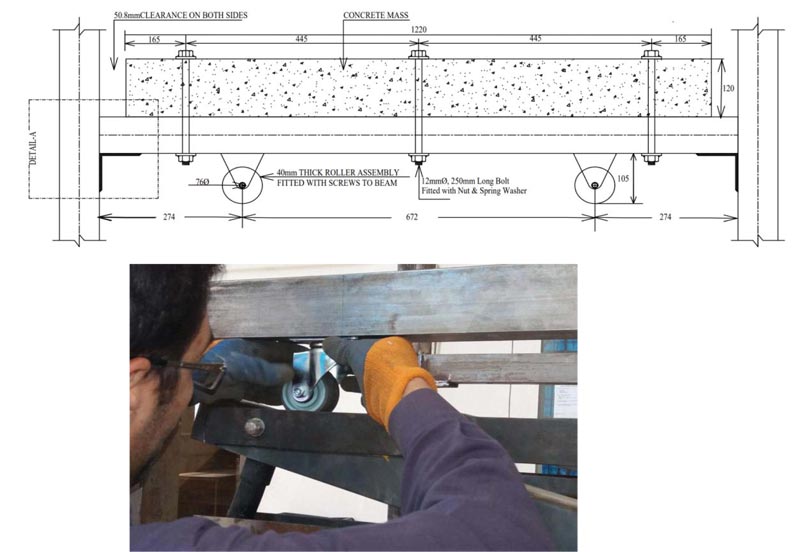
In order to impart the structural deformation and activate the proposed sliding level technique during lateral shaking, rollers were provided at the base of structural beams, which were in direct contact with the ramp beams, as shown in Fig. (7). The rollers were provided so that when one end of the ramp tries to compress, the other end will tend to rise due to the lever arm mechanism. The function of rollers is to take the horizontal lateral drift and tends to transform or dissipate it through the vertical motion of the damper. The rollers were installed on the bottom faces of the structural beams using epoxy glue. It should be noted that there should be no gap between the ramp beam and rollers in order to avoid any impact of shaking on the non-structural frame during lateral shakings. For this purpose and during the fabrication of the test specimen, first the rollers were fixed to the bottom faces of the structural frame beam, and after that, the ramp and damper assembly was provided with full contact with respective rollers.

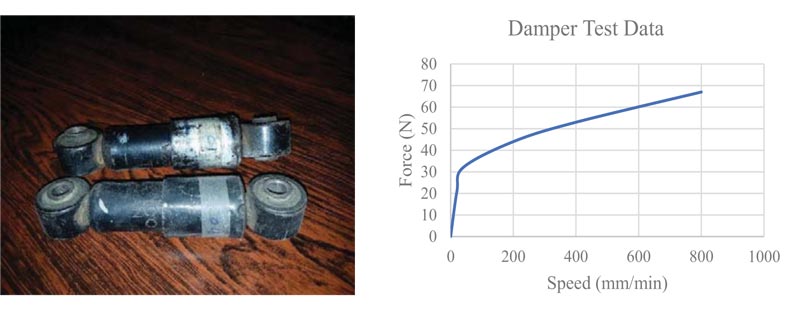
For dampers, locally available small size fluid dampers were used that can be easily installed in the proposed energy dissipation configuration, as shown in Fig. (8). Fig. (8) also shows the force-speed relationship of the installed dampers. It is also worth mentioning that, due to the reduced size scaling of the test specimen, the reduced model will act by reducing seismic loading. For this purpose, to have the same frequency range, as compared to the prototype frame structure, an extra mass of 520 kg was provided to theform reinforced concrete slab during the shake table testing. The size of the provided slab was 1600.2 mm (5.25 feet) in length, 1118.62 mm (3.67 feet) in width, and with a thickness of 120.65 mm (4.75 in). Predefined holes in the slab were provided during the casting of concrete, in order to fix the slab mass over the structural frame beams through steel screws, as shown in Fig. (9). During the experimental testing, the dead load and additional seismic weight were provided to the form RCC slab to ensure rigid diaphragm behavior. For this purpose, the RC slab was rigidly screwed to beams at each story level. Fig. (9) also shows the test model joint detailing.

3.3. Shake Table test of Test Specimen

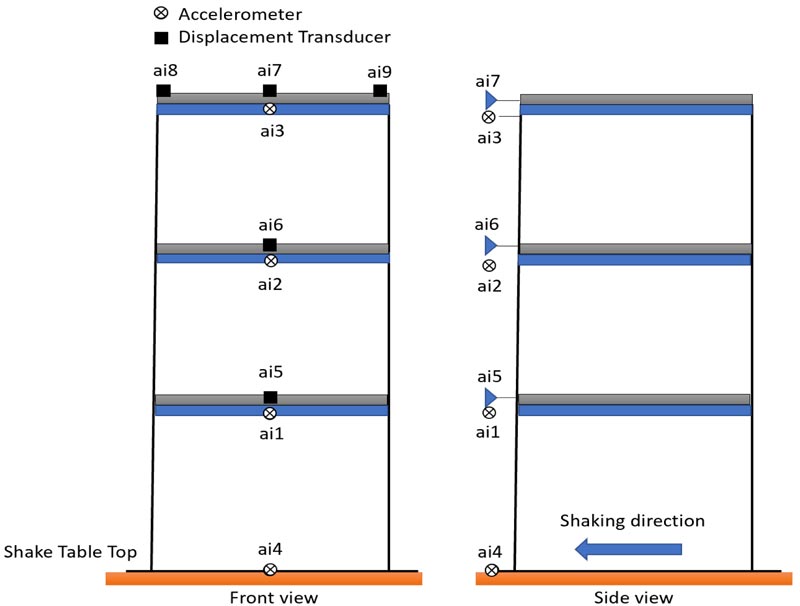
Fig. (10) shows the test model set up on the uni-directional shaking simulator of Earthquake Engineering Center EEC, University of Engineering and Technology Peshawar. As the objective and scope of the experimental study were to check the feasibility of the proposed damping mechanism, only in-plane direction of the test model was considered and tested in uni-directional lateral excitation, as shown in Fig (10). For out-of-plane and/or bi-directional excitations, the same configu- ration may be provided in the orthogonal direction of the structural frame. The test model was instrumented with five linear variable displacement transducer LVDTs and four accelerometers to record the frame displacement and acceleration records for each excitation. Three accelerometers were installed on the first, second and third story level, mid position, and one accelerometer was installed on the shaking tabletop. Similarly, three LVDTs on each story level, mid position and two extra LVDTs on the third story extreme edges were installed. Fig. (11) shows the test frame instrumentation layout; whereas, Fig. (12) shows the input acceleration records used for shaking. The experimental model was tested for acceleration records of Imperial Valley 1979 accelerogram, after careful analysis of a number of acceleration records to be within the limits of shaking simulator. Table 1 reports the sequence of input excitation applied to the damped and undamped test models. During the testing of the undamped frame system, the attached rollers were removed from the structural frame, and the test frame was excited with same excitation runs. The test models were excited with increasing PGA with 10%, 20%, 30%, 40%, 50% and 60% of the input excitation, with and without the sliding lever energy dissipation technique. During each test run, the frame model was inspected for any localized damages in the structural frame column and beam members. At the end of Run No.12, the shake table ran into severe self-check excitation, during which the column at the base and joint regions were observed with local buckling damages. After this run, the testing sequence was stopped.

Table 1.

Run No.	Scale	Sliding Lever Damping Configuration Installation
1	0.1g	YES
2	0.2g	YES
3	0.3g	YES
4	0.4g	YES
5	0.1g	NO
6	0.2g	NO
7	0.3g	NO
8	0.4g	NO
9	0.5g	YES
10	0.5g	NO
11	0.6g	YES
12	0.6g	NO

4. RESULTS AND DISCUSSION

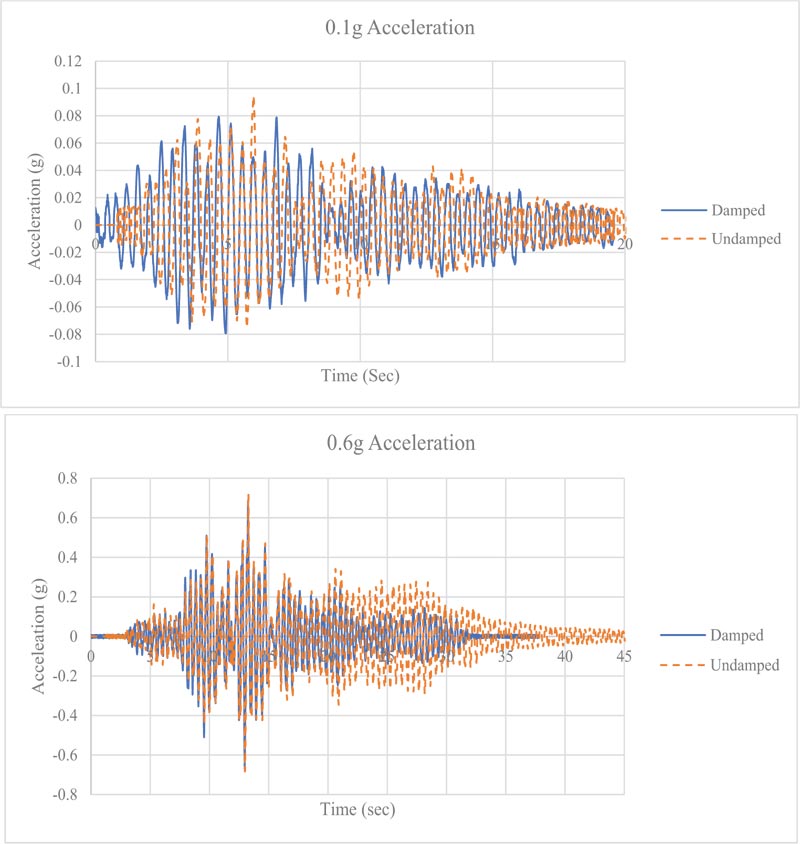
The recorded data obtained from install instrumentation, in the form of acceleration and displacement records, were further processed using signal analysis software DADISP, in order to perform data filtering and to remove any noise during the experimental shaking. Once all the data has been processed, the displacement and acceleration time histories for each run and with and without sliding lever damper technique have been obtained and used for comparison. Fig. (13) and Fig. (14) show the acceleration and displacement response history of the test frame for the 0.1g and 0.6g input excitation and with and without sliding damper configuration. For the damped and undamped cases, the acceleration and displacement time histories showed a similar response with lesser peak values for damped configuration. Fig. (15) shows the peak displacement response with increasing exaction PGA inputs, whereas Fig. (16) shows the structural response spectrum for different input excitations. As shown in Fig. (13) and Fig. (15), in the case of 0.2g shaking excitations, the top story peak displacement obtained for the undamped and damped cases was 18.10 mm and 11.17 mm, respectively, showing a decrease in the peak displacement values by an amount of about 36.55%. Similarly, in the case of 0.6g shaking excitations, the top story peak displacement obtained for the undamped and damped cases was 79.60 mm and 70.00 mm, respectively, showing a decrease in the peak displacement values by about 12.06%. Similarly, the maximum acceleration for the damped frame, at the third story, decreased by 55% and 6%, respectively. The top story peak displacement response with increasing PGA, shown in Fig. (15), demonstrated the reduction of displacement response due to the energy dissipation of sliding lever mechanism. Due to the sliding lever damping technique, the top story peak displacements for the damped frame case decreased by 36.55% in case of 0.1 g, 37.95% in case of 0.2g, 31.89% in case of 0.3g, 38.05% in case of 0.4g, 29.37% in case of 0.5g and 12.06% in case of 0.6g shaking excitation.

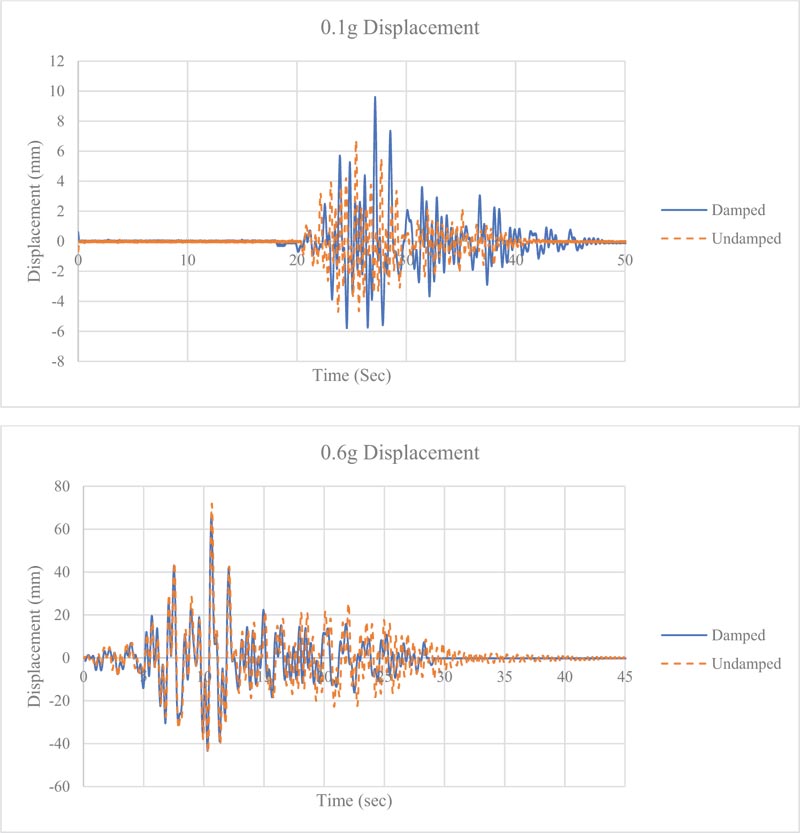
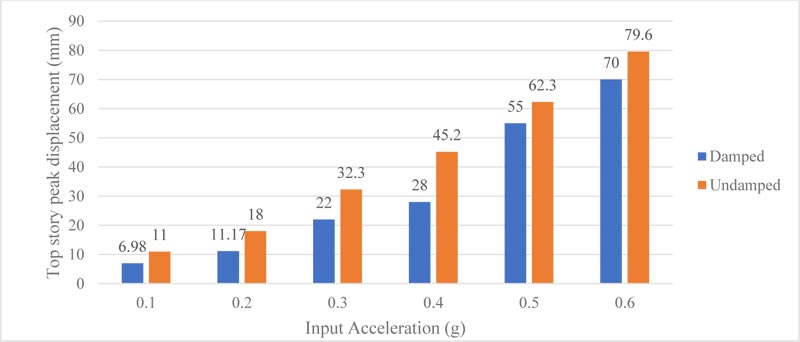
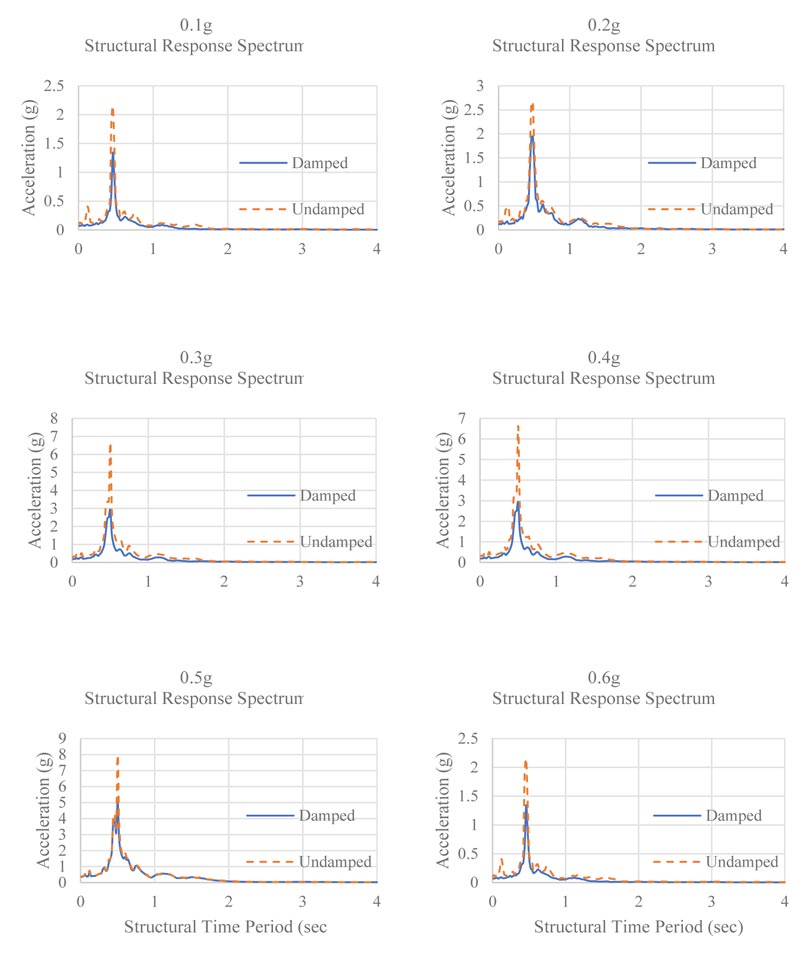
It is evident from Fig. (13) to Fig. (14) that displacement and acceleration response differences are quite significant during the initial elastic stage, which decreases with increasing input excitations. It has been observed from the shaking test of the proposed sliding lever energy dissipation configuration that with the increase in shaking excitations, the damping mechanism becomes less efficient, leading to a small decrease in the displacement and acceleration response. The sliding lever mechanism shows a good behavior in controlling displacement and acceleration response in low excitation shaking, whereas with an increase in the shaking level, the damping technique seems to be less efficient. This can be attributed to the installed damper characteristics having low energy dissipation at higher velocity levels, as shown in Fig. (8). As shown in this study, locally available dampers that can be easily fixed in test model configuration have been utilized in order to check the feasibility of proposed energy dissipation sliding technique. Due to shake table limitations, such as reduced model size and use of locally available small size dampers, the dissipation mechanism at high acceleration excitation values seems less efficient. It is believed that, with a further optimized size damper, the configuration can be made more effective in high shaking demands. Fig. (16) shows the test model response spectrum with increasing shaking excitations and corresponding damping value, showing an increase in damping values and no frequency variations with the energy dissipation sliding lever mechanism.

CONCLUSION

A novel energy dissipation mechanism using a sliding lever damping technique has been proposed and experimentally investigated through the shake table test. The new damping configuration mechanism aims to avoid the structural members and connection regions to resist any extra loading as seen in other passive braced type energy dissipation techniques. For this purpose, a non-structural frame supporting the ramp-damping assembly has been provided to check the feasibility of the proposed configuration. A 1/3^rd scaled reduced test specimen has been fabricated and tested dynamically in a uni-directional excitation without and with the new configuration.

The following important findings and conclusions have been obtained based on the shake table test performed:

1. It has been confirmed from the current experimental study that the new configuration was quite effective in reducing the overall displacement and acceleration response. The reduction in the structural response parameters was very significant during low excitations shaking, whereas, with the increase in shaking intensities, the responses varied with much less difference.
2. The top story peak displacements for the damped frame case decreased by 36.55% in case of 0.1 g, 37.95% in case of 0.2g, 31.89% in case of 0.3g, 38.05% in case of 0.4g, 29.37% in case of 0.5g and 12.06% in case of 0.6g shaking excitations, as compared to the structure without sliding damping configuration.
3. The roof/top story maximum acceleration for the damped frame case decreased by 55% in case of 0.2g and 6% in case of 0.6g shaking excitations as compared to the structure without sliding damping configuration.
4. The damping ratios for the damped model case showed an increase of about 70% in case of 0.1g and 22% in case of 0.6g excitation, as compared to the structure without sliding damping configuration.
5. It has been observed from the current experimental study that the new sliding lever energy dissipation configuration does not change the frequency of the structural frame, and thus stiffness of the main frame remains the same.

REFERENCES