All published articles of this journal are available on ScienceDirect.
Ground Movements Prediction in Shield-Driven Tunnels using Gene Expression Programming
Abstract
Introduction:
The increase in population and traffic in metropolitan areas has led to the development of underground transportation spaces. Therefore, the estimation of the surface settlement caused by the construction of underground structures should be accurately considered. Several methods have been developed to predict tunneling-induced surface settlement. Among these methods, artificial intelligence-based methods have received much attention in recent years. This paper is aimed to develop a model based on Gene Expression Programming (GEP) algorithm to predict surface settlement induced by mechanized tunneling.
Methods:
For this purpose, Tehran Metro Line 6 was simulated numerically to investigate the effects of different parameters on the surface settlement, and 85 datasets were prepared from numerical simulations. Subsequently, several GEP models were implemented using the obtained datasets from numerical simulations and finally, a model with 30 chromosomes and 3 genes was selected as the optimum model.
Results:
A comparison was made between obtained maximum surface settlements by the proposed GEP model and numerical simulation. The results demonstrated that the proposed model could predict surface settlement induced by mechanized tunneling with a high degree of accuracy.
Conclusion:
Finally, a mathematical equation was derived from the proposed GEP model, which can be easily used for surface settlement prediction.
1. INTRODUCTION
The demand for underground spaces and facilities is increasing because of population increment and the lack of urban spaces. The underground structures in urban areas are usually excavated in soft soils beneath surface buildings and underground utilities, therefore, the excavation of tunnels should be controlled within the permissible range of surface settlement [1]. The shield-driven method is extensively used in urban areas with the aim of reducing ground movements induced by tunnel excavation and as well as increasing tunneling advance rate. The Earth Pressure Balance (EPB) is the most applied shield tunneling machine to tunnel construction for subway lines because of its ability to work in various geological conditions.
Surface settlements in mechanized tunneling are usually resulted from three ground movements including, movement in the tunnel face, movements on the shield shell due to the difference in the outer diameter of the cutter head and tail skin (shield skin gap), and finally movements at the shield tail due to the difference between the diameter of the shield tail (tail void gap) and tunnel lining [2]. Fig. (1) shows the contribution of the influential parameters on tunneling-induced surface settlements. According to this figure, the contribution of deformations in the tunnel face is between 25 and 30 percent [3].
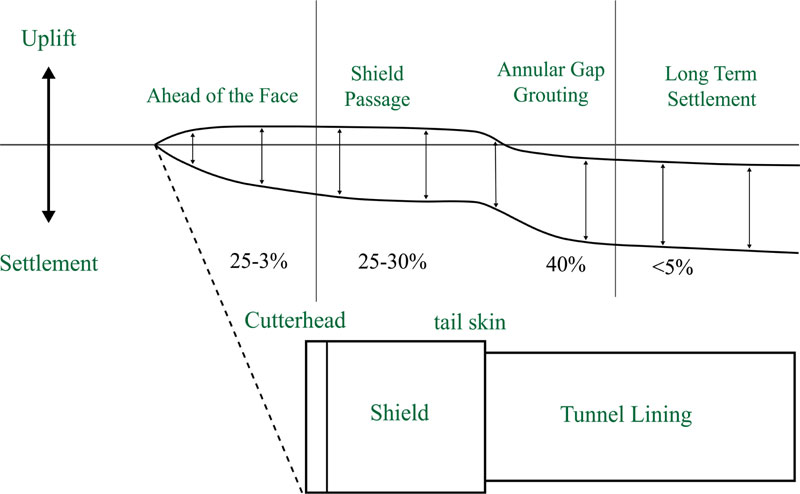
Prediction is the first step to prevent the undesirable ground movements induced by tunneling. A precise prediction of surface settlement in mechanized tunneling is very complex and depends on parameters, such as tunnel geometry, soil mechanical properties as well as operational parameters. The tunneling-induced surface settlement can be evaluated by analytical, experimental and numerical methods, as has been done in the Istanbul metro [4]. Although extensive experiments have been conducted around the world to design and build the tunnel, however, few empirical relationships developed to precisely predict surface settlement [5, 6].
Analytical approaches, among the prediction methods, are less reliable because of simplifications and ignoring some parameters. Numerical methods are time-consuming and need high skill for prediction. In the meantime, artificial intelligence-based methods have significantly been developed to solve problems that are difficult to solve by analytical and numerical methods [7-9]. Artificial intelligence-based methods have been widely used in many geotechnical aspects [10-14]. These methods have also been used to predict tunneling-induced ground movements [15-20].
Gene expression programming (GEP), as a powerful intelligence method, has recently widely been used in many researches. The great advantage of this method, among other artificial intelligence-based methods, is the ability to extract a relationship between given data, whereas other ordinary artificial intelligence approaches have not this ability [21]. This method was used in many geotechnical subjects such as predicting crest settlement in concrete face rockfill dams [22], settlement prediction of shallow foundations on cohesionless soils [23], prediction of crest settlement of concrete-faced rockfill dams [24], settlement prediction of rock-socketed piles [25], predicting tunnel convergence [21], performance prediction of tunnel boring machine [26] and roadheader performance prediction [27].
This study is aimed to present a mathematical relationship to predict the maximum surface settlement due to EPB tunneling. For this purpose, Tehran Metro Line 6 was investigated as the case study. First of all, 2D numerical simulations in two forms of axial symmetry and plane strain were conducted and all effective parameters on surface settlement were considered. Subsequently, effective parameters on surface settlement were changed in an acceptable range in the numerical models. Finally, a GEP model was developed by using the obtained database from numerical simulations and a mathematical relationship was proposed to predict surface settlement induced by EPB tunneling.
2. MATERIALS AND METHODS
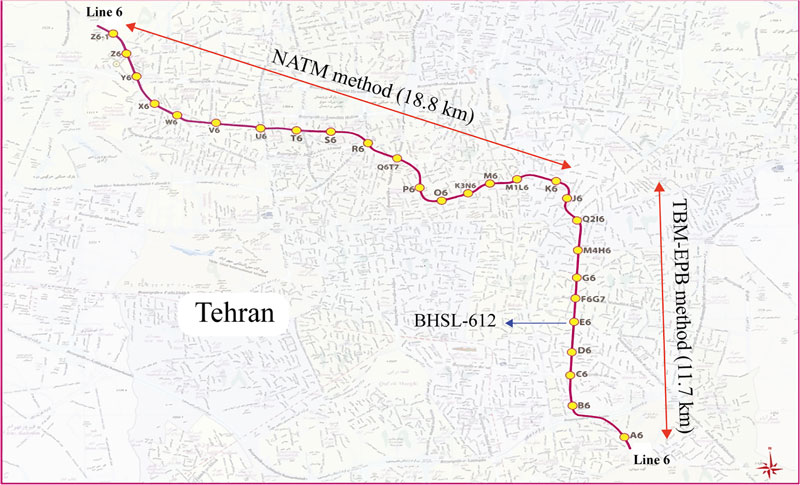
Line 6 of Tehran Metro is one of the longest metros in Iran that connects southeast of Tehran to its northwest. Its original design had 30 km long and consisted of 28 stations, with nine stations intersecting with the other seven subway lines. By recent developing of the south of this line, Line 6 has 38 km long with 31 stations and is currently the longest subway line in the Middle East. The plan for this line shown in Fig. (2).
According to the existing topographic maps, the project area is approximately located at the level in the range from 1085 to 1391 m above sea level. Tehran's alluvial sediments are mainly the result of rivers and seasonal floods originating from the northern highlands, located in central Iran, which is about 650 meters above sea level.
The changes in climate and tectonic regimes have directly affected the status of the surface water inflows and their sediment transport over time. It has induced deposition of coarse-grained and fine-grained soils. More coarse-grained soils can then be found in the northern parts of Tehran rather than its southern parts. The result of the feldspar alteration and weathering are clay minerals, i.e. Illite and Kaolinite. The crushing and erosion of quartzes mostly result in sandy elements and thus tuffs provide fine-grained materials and alluviums [28].
The soil properties of the borehole BHSL-612 is tabulated in Table 1 which is one of the critical sections of this line.
Tunnel excavation in various parts of a project can be conducted using several methods. Some parameters such as the topography, tunnel length, operational conditions, groundwater level, interference with underground urban facilities and presence of commercial and residential buildings are limiting parameters in excavation method selection. Considering the mentioned parameters, two most famous methods of mechanized tunneling as well as new Austrian tunneling method (NATM) were selected to be used in the excavation of Line 6 of Tehran Metro. In this regard, the southern part of this line is excavated using EPB Tunneling and the middle and northern parts are excavated by NATM.
The EPB part of the tunnel was selected as the case study. The outer diameter of the tunnel lining is 8.85 m. The support of the tunnel excavated by the EPB machine is conducted using the precast reinforced concrete segments where each ring consists of eight pieces and a key. Each ring has 1.5 m long and 0.35 m thickness. Table 2 shows the mechanical properties of the precast segmental lining of the case study.
3. NUMERICAL SIMULATION
In this study, FLAC 2D V.8 was used to simulate the excavation of the Tehran Metro Line 6 tunnel. In the numerical simulation, model dimensions should not be considered very small to affect the simulation results and not very large to increase the model analysis time. In this paper, the model length and height are considered to be 140 m and 68 m, respectively. The Mohr-Coulomb failure criterion was used to simulate the surrounding soil of the tunnel and the isotropic elastic behavior model and beam structural element were used to simulate the tunnel support system. The diameter of the tunnel is equal to 8.85 m. There are crossroads on the tunnel cross-section at the ground surface. Therefore, the surface load of 20 KPa equivalent to the traffic load was applied.
| Parameter | Symbol | Value | Value | Unit |
|---|---|---|---|---|
| Layer | L | Sandy clay | Clayey Sand & Gravel | - |
| Depth | H | 9 | 68 | m |
| Dry volume weight | γ dry | 1710 | 1700 |
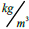
|
| Saturated volume weight | γ saturation | 2100 | 2100 |
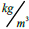
|
| Young's Modulus of the MC model | E | 15 | 100 | MPa |
| Poisson's ratio of MC model | v | 0.4 | 0.35 | - |
| Cohesion | C | 35 | 30 | kPa |
| Angle of internal friction | Øo | 28 | 30 | degree |
| Coefficient of earth lateral pressure | Ko | 0.5 | 0.65 | - |
| Uniaxial compressive strength | Poisson's ratio | Young's Modulus | Density |
|---|---|---|---|
| fc (MPa) | v | E(MPa) |
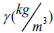
|
| 35 | 0.2 | 27800 | 2500 |
According to Fig. (1), considering the 25 to 30 percent effects of tunnel face deformation on the surface settlement, the effect of the face pressure should also be considered in the two-dimensional numerical simulation. Consequently, the longitudinal profile of the tunnel was simulated in addition to its cross-section. The boundary conditions, element size and numerical model of the tunnel cross-section is shown in Fig. (3). In addition, the numerical model of the tunnel in the longitudinal profile is presented in Fig. (4). Quad mesh (zone) is used in numerical modeling for the ground.
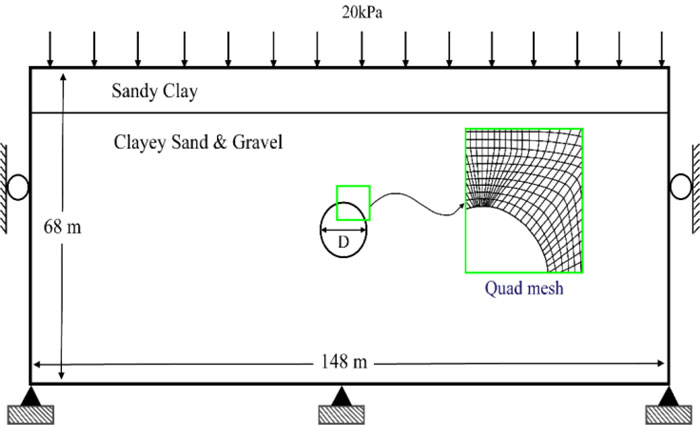
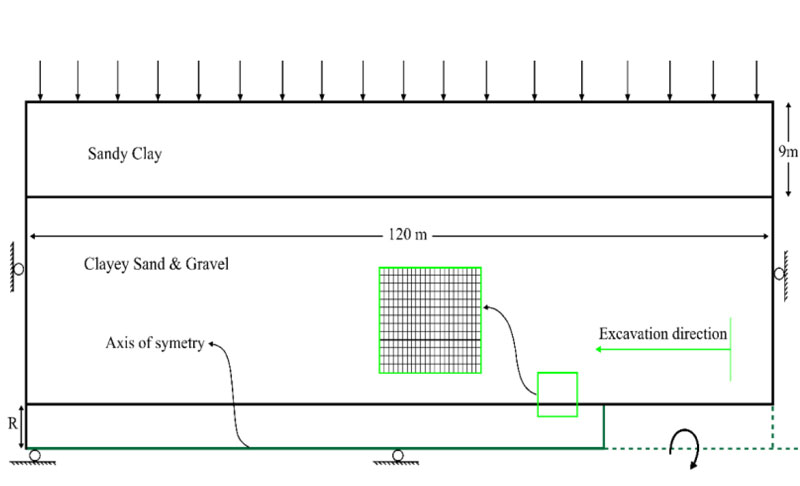
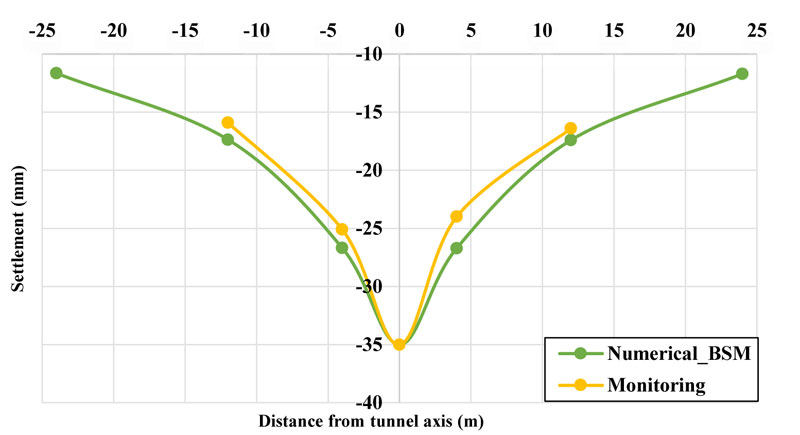
The surface settlement attained by using the numerical model was back analyzed using the surface monitoring results to calculate an adequate stress relaxation factor. The maximum surface settlement obtained from the survey is for the cross - sectional is using to calibrate the amount of stress relaxation in the two-dimensional model, which is initialized with reality. It is the cause that the maximum surface settlement attained by the numerical model is in very good agreement with the monitoring result. In addition, the obtained settlement curve is also in good agreement with the monitoring data, as shown in Fig. (5).
Subsequent to initializing the numerical results, a parametric analysis was conducted to prepare the datasets for GEP analysis. In this regard, 85 numerical models were constructed for various conditions, including tunnel diameter and depth, elasticity modulus, cohesion, Angel of internal friction, grouting pressure and surface loads. The effect of tunnel face pressure also simulated in the longitudinal profile and the obtained settlements were added to the obtained settlements from transversal section modeling. The range of the parameters used in numerical simulations and maximum surface settlements are tabulated in Table 3.
4. GENE EXPRESSION PROGRAMMING
Gene expression programming was proposed by Ferreira [30] based on the combination of genetic algorithm (GA) and genetic programming (GP). In GEP, the individuals are implied as the fixed-length strings called “chromosomes”. The chromosomes are then stated as non-linear entities of different sizes and shapes named expression trees [31].
In GEP, mathematical equations are defined as chromosomes. GEP has two main components called chromosomes and Expression Tree (ET). A chromosome, in which some information is coded using a specific language, may contain one or more genes. Any mathematical information in the gene on the chromosomes is encoded by the KARVA language and translated into the expression trees by the ET language [32]. Chromosomes are composed of two main elements of terminal and function, the terminals being input variables or constants that are chosen by the designer and the functions being mathematical operators (+, −, ×, ∕, sin, Log, etc.). The main components of GEP include terminal set, function set, fitness function, genetic operators, and stopping criteria. Each gene has two head and tail segments, whereas the functions and terminals can be located in the head. While the tail only includes terminals. The head length of the (h) segment is specified by the user and the length (t) of the tail is determined by h and the number of function arguments, as in Equation (1).
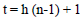 |
(1) |
Where, n is the arguments number of the function.
| Parameter | Unit | Symbol | Type | Max. | Min. | Mean |
|---|---|---|---|---|---|---|
| Tunnel diameter | m | D | Input | 10.85 | 3.85 | 8.78 |
| Tunnel depth | m | H | Input | 132.75 | 13.27 | 34.35 |
| Elasticity Modulus | MPa | E | Input | 1000 | 10 | 198.9 |
| Cohesion | kPa | C | Input | 550 | 10 | 49.6 |
| Internal friction angle | ◦ | Φ | Input | 60 | 0 | 30 |
| Grout pressure | kPa | P | Input | 500 | 1 | 162.5 |
| Surface load | kPa | L | Input | 150 | 10 | 30.5 |
| Face pressure | kPa | F | Input | 500 | 60 | 297.2 |
| Settlement | cm | S | Output | 8.49 | 1.80 | 2.62 |
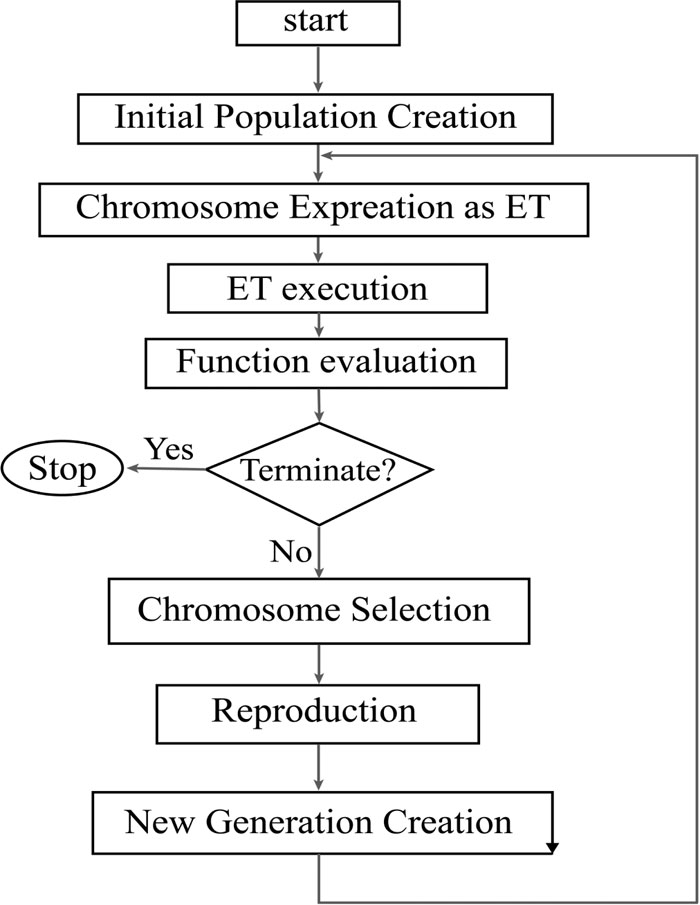
The first step in GEP is to generate the initial population of solutions which can be conducted by a random process or by considering input information about the problem. The chromosomes are then expressed as a tree expression and evaluated by the fitting function. If the desired solution is reached or the generations reach a certain number, evolution is terminated and the best solution is offered. If no stopping conditions are found, the selection is done and the rest of the solutions are assigned to a selection process. This process is repeated for several generations and the quality of the population improves as well [33]. To evaluate the performance of the model, a series of statistical indices are used, including root mean square error (RMSE), mean absolute error (MAE) and correlation coefficient (R2), as in Equations (2) to (4). Fig. (6) presents a schematic view of the GEP algorithm.
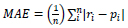 |
(2) |
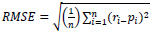 |
(3) |
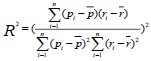 |
(4) |
where i is the data number, r is the actual value of the maximum surface settlement, p is the predicted value of the maximum surface settlement, r̅ and p̅ are the means of actual and predicted values of maximum surface settlement, respectively, and n is the number of data sets.
5. RESULTS AND DISCUSSION
In this study, GeneXproTools V.5 was used to predict the surface settlement induced by tunneling through the GEP algorithm. In this regard, the total of 85 datasets obtained from numerical simulations including 8 input parameters and 1 output parameter were used. From these datasets, 57 datasets (67%) were used for training and 28 datasets (33%) for validation. The RMSE was also considered as the fitness function. Table 3 shows the range of input and output data.
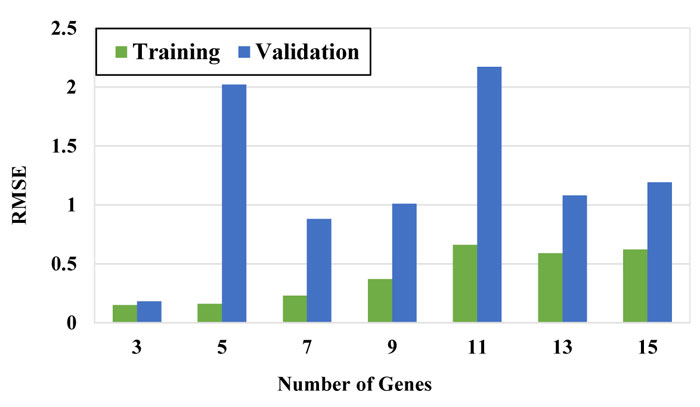
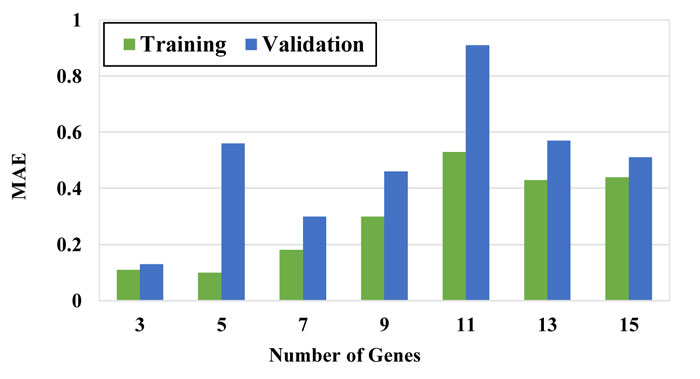
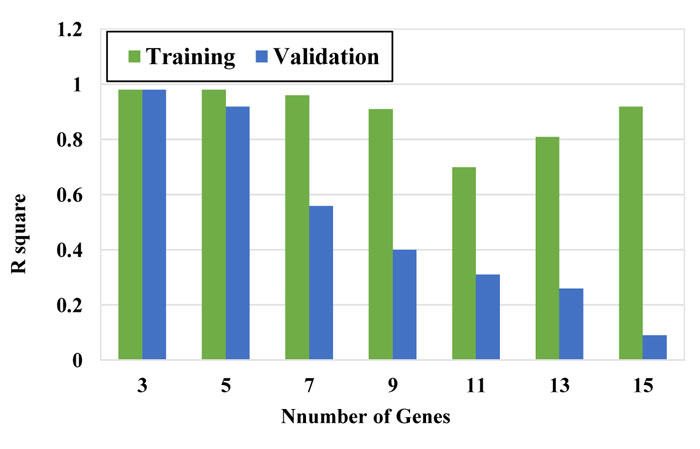
To obtain the best model, the number of chromosomes and number of genes were selected using the trial-error method by changing them within a large range. Figs. (7-9) show the performance of the models with a different number of chromosomes. While other parameters were considered constant, the optimal number of chromosomes was selected based on the minimum error and maximum correlation. The function that has the minimum RSME and MAE is selected as the optimal function.
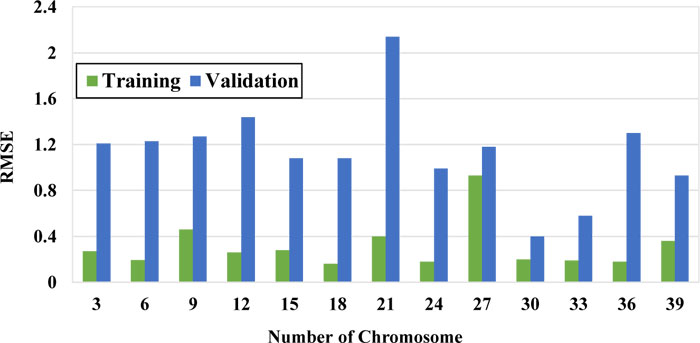
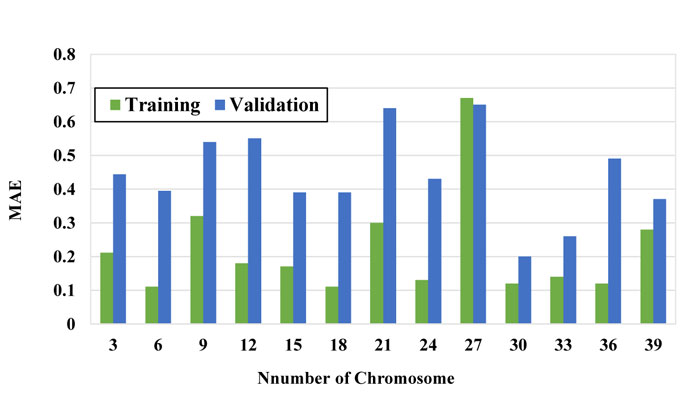
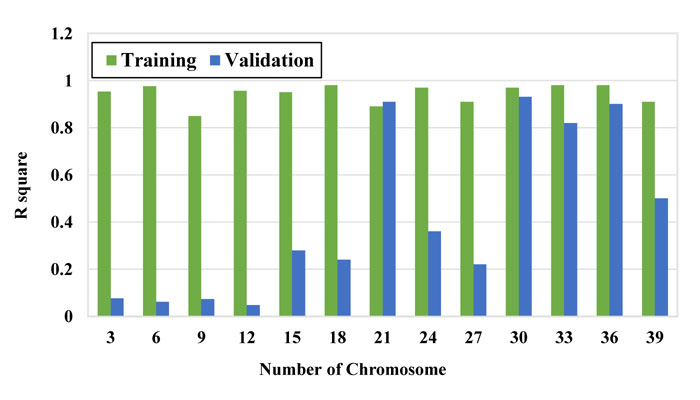
As it can be seen in these figures, the model with 30 chromosomes yields the minimum RSME and MAE and maximum R2 for both training and validation datasets. Therefore, number of 30 chromosomes was selected to be used in modeling.
In the next step, several modeling was performed with a chromosome number of 30 with different genes. The results are presented in Figs. (10-12). Based on the RMSE, MAE and R2 values, the model with 3 genes presented the best performance among other models and therefore, the model with 30 chromosomes and 3 genes was selected as the final model. The configuration of the selected GEP model is tabulated in Table 4.
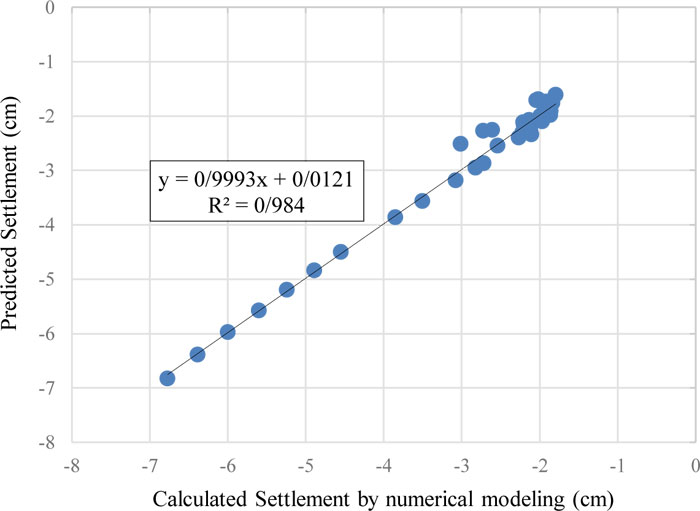
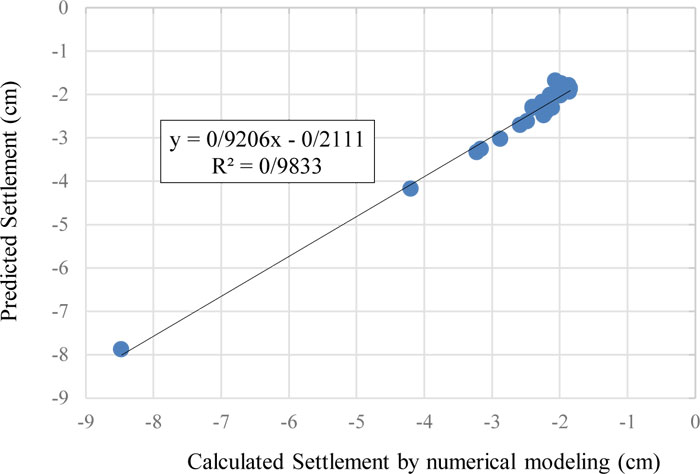
Table 5 presents the results of the proposed model for predicting the maximum surface settlement due to tunneling According to this table, values of R2 for training and validation datasets are above 0.98 that the proposed model is able to predict surface settlement with a high degree of accuracy. Comparisons between the obtained surface settlement by the proposed GEP model and numerical simulation for training and testing datasets are shown in Figs. (13 and 14), respectively.
| Number of Chromosomes | Head Size | Number of Genes | Connection Function | Constants per Gene | Function Set |
|---|---|---|---|---|---|
| 30 | 8 | 3 | Addition | 2 | +, -, ÷, ×, exp, Ln, log, x2, tan, inv |
| MAE | RMSE | R2 | Role |
|---|---|---|---|
| 0.11 | 0.15 | 0.984 | Training |
| 0.13 | 0.18 | 0.983 | Validation |
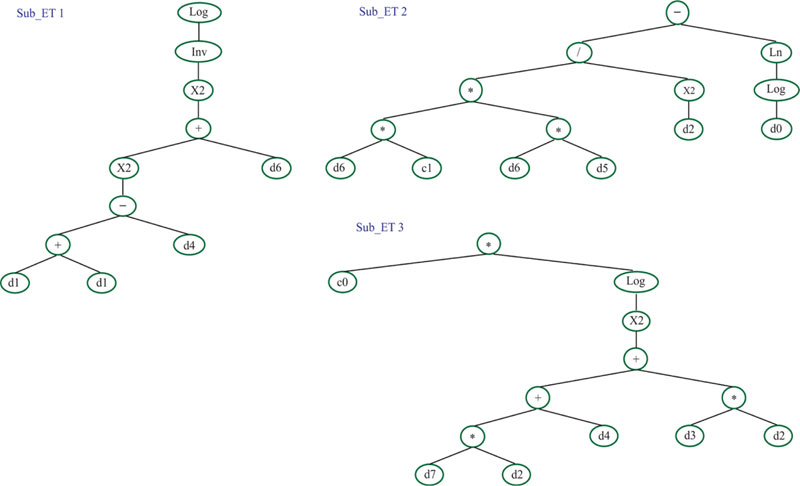
Fig. (15) presents the expression tree for the suggested GEP model, whereas Equation (5) was extracted from this figure. Fig. (15), in fact, presents the derived relationships between input and output data by using the GEP algorithm. This feature of the GEP algorithm makes its results more applicable compared to other artificial intelligence techniques.
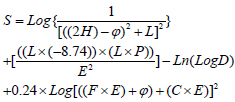 |
(5) |
where S is the maximum surface settlement (cm), H and D are tunnel depth and diameter (m), respectively, E is the modulus of elasticity (MPa), C is the cohesion force (KPa), φ is the internal friction angle of soil (°), P and F are grout pressure and face pressure (KPa), L is ground surface load (KPa).
CONCLUSION
A GEP model was developed with the aim of predicting surface settlement caused by mechanized shield tunneling. To achieve this goal, 85 datasets were prepared using numerical simulation of the Tehran Metro Line 6 project. To develop a GEP model, 57 datasets were used for training, and 28 datasets were used to validate the results. Each dataset contains eight input parameters, including tunnel diameter, tunnel depth, elasticity modulus, cohesion, internal friction angle, grout pressure, tunnel face pressure and surface loads. The output parameter was the maximum surface settlement. The RMSE fitness function was also selected to evaluate the modeling performance. By the trial-error method, several GEP models were implemented and finally, an optimal model with 30 chromosomes and 3 genes was selected to be used for maximum settlement prediction. Based on the obtained results, it can be concluded that the proposed GEP model is a reliable tool to predict maximum surface settlement induced by mechanized shield tunneling.
NOTES
1 Department of Mining, Faculty of Engineering, Urmia University, 5756151818 Urmia, Iran. Email: a.ramesh4735@gmail.com
2 Department of Mining, Faculty of Engineering, Urmia University, 5756151818 Urmia, Iran. Email: m.hajihassani@urmia.ac.ir; mohsen_hajihassani@yahoo.com, Contact No: +989122735914 (Corresponding Author).
3 Department of Mining, Faculty of Engineering, Urmia University, 5756151818 Urmia, Iran. Email: alireza.rashiddel@gmail.com
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


