All published articles of this journal are available on ScienceDirect.
Soil Unconfined Compressive Strength Prediction Using Random Forest (RF) Machine Learning Model
Abstract
Aims:
Understanding the mechanical performance and applicability of soils is crucial in geotechnical engineering applications. This study investigated the possibility of application of the Random Forest (RF) algorithm – a popular machine learning method to predict the soil unconfined compressive strength (UCS), which is one of the most important mechanical properties of soils.
Methods:
A total number of 118 samples collected and their tests derived from the laboratorial experiments carried out under the Long Phu 1 power plant project, Vietnam. Data used for modeling includes clay content, moisture content, specific gravity, void ratio, liquid limit and plastic limit as input variables, whereas the target is the UCS. Several assessment criteria were used for evaluating the RF model, namely the correlation coefficient (R), root mean squared error (RMSE) and mean absolute error (MAE).
Results:
The results showed that RF exhibited a strong capability to predict the UCS, with the R value of 0.914 and 0.848 for the training and testing datasets, respectively. Finally, a sensitivity analysis was conducted to reveal the importance of input parameters to the prediction of UCS using RF. The specific gravity was found as the most affecting variable, following by clay content, liquid limit, plastic limit, moisture content and void ratio.
Conclusion:
This study might help in the accurate and quick prediction of the UCS for practice purpose.
1. INTRODUCTION
Soil science is a complex discipline that involves fundamental and applied aspects of soil biology, soil physics and soil chemistry [1]. In civil engineering, understanding the mechanical properties of soils in a relationship with the applications is of fundamental importance [2]. Soil mechanics allows engineers to explore the properties and behaviors of soils, so that an adequate solution to given problems could be granted. While treating settlement or damage problems, soil science is important as many construction works are directly affected by the soil mechanics studies, including building, bridges, road, railway, tunnels and dams. Various investigations related to this field have been conducted, for instance, soil mechanical properties [3], permeability of fractured porous media [4-6], consolidation of soil [7-8] and especially the compressive strength of soil.
Indeed, soil Unconfined Compressive Strength (UCS) is an important factor which is used to validate the compaction ability of soil [9]. It can be directly determined in the laboratory through unconfined compression test. However, this test usually takes a long time and is costly, which might increase construction costs. Moreover, the accuracy of such a test depends significantly on the quality of equipment or the experimenter. It is thus necessary to find an alternative and effective way to predict the soil UCS. The use of machine learning algorithms has spread rapidly over the last decades, especially in computer science. Such approach provides a possibility to learn information from data, which is an attractive alternative compared with “manual” learning [10]. In civil engineering, machine learning algorithms have been applied to solve countless real-world problems, such as landslides [11-13], floods [14], weather and climate [15-17], materials science [18-23], engineering structures [24-26] or soil properties [27]. In general, the machine learning approach is promising and potential for accurate and fast prediction of soil properties.
Despite the fact that Random Forest (RF) is one of the most popular and effective machine learning algorithm, limited research has investigated the possibility of using RF in predicting the Soil Unconfined Compressive Strength. In this work, the RF algorithm was developed to investigate the feasibility of applying such a model for quick estimation of the Soil Unconfined Compressive Strength. For this, a total number of 118 samples was collected from Long Phu 1 power plant project and laboratory experiments were carried out to determine the soil properties. The database included input parameters such as clay content, moisture content, specific gravity, void ratio, liquid limit, plastic limit and one output variable, the Unconfined Compressive Strength (UCS). To validate the performance of RF, several assessment criteria were used, namely the correlation coefficient (R), root mean square error (RMSE) and mean absolute error (MAE). Using RF, feature importance analysis of input parameters in predicting the UCS was also conducted with the aim of providing better insights into the problem.
2. DATA COLLECTION AND ANALYSIS
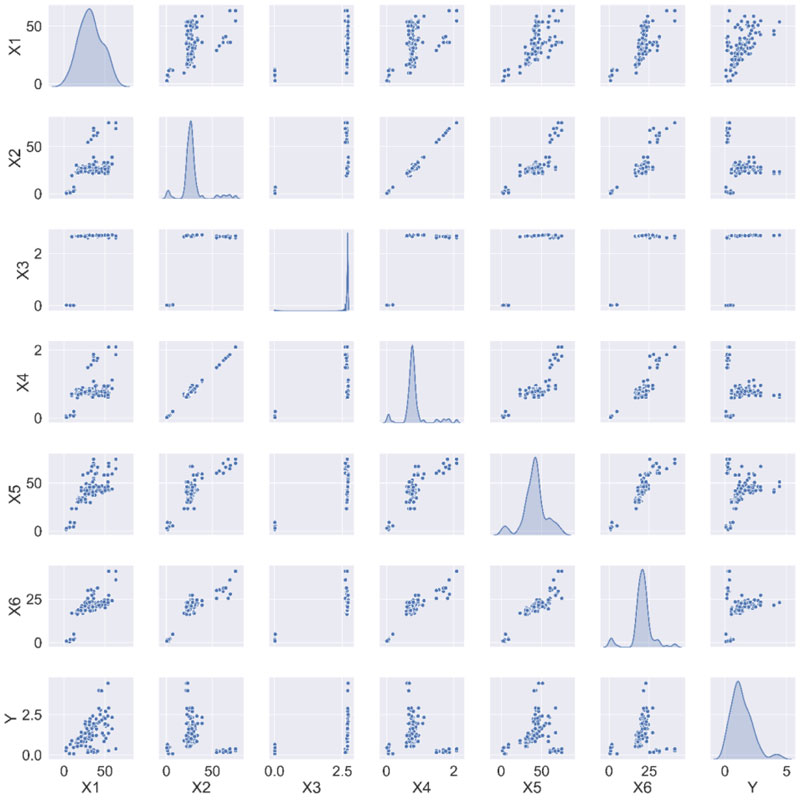
In this study, soil samples were collected from the Long Phu 1 power plant project, located in Soc Trang province, Vietnam. Laboratory tests of 118 soil samples were carried out to determine the soil properties used for the design and construction of the project, and used to generate the training (70%) and testing (30%) datasets for the development of the RF model. In the datasets, there were six soil properties, including the clay content (%), void ratio, liquid limit (%), moisture content (%), plastic limit (%), and specific gravity. They were used as input parameters of the RF model. Besides, the UCS (or qu), determined by using unconfined compression tests in laboratory conditions, was used as an output parameter. Detail description of these parameters can be found in the work of Das and Sobhan [28]. A correlation analysis of the inputs was carried out and presented in Fig. (1). It can be observed that the value of clay content ranging from 2.4-63.4 mm, with an average and median values of 32.63, 31.55, respectively, and a standard deviation of 13.85. The value of moisture content ranging from 0.61-75.14%, with an average and median values of 28.66, 26.42, respectively, and a standard deviation of 13.46. The value of specific gravity ranging from 0.01-2.72, with an average and median values of 2.53, 2.69, respectively, and a standard deviation of 0.64. The value of the void ratio ranging from 0.017-2.089, with an average and median values of 0.83, 0.78, respectively, and a standard deviation of 0.36. The value of the liquid limit ranging from 1.6-74.9%, with an average and median values of 41.54, 42.0, respectively, and a standard deviation of 14.30. The value of plastic limit ranging from 0.6-41.0%, with an average and median values of 20.64, 20.75, respectively, and a standard deviation of 6.31. Finally, the UCS ranging from 0.078-4.43 kG/cm2, with an average and median values of 1.37, 1.21, respectively, and a standard deviation of 0.87.
It can be seen that for all the variables, the median values were very close to the average values, representing that such variables could be approximated by a normal distribution. The inter-correlation between inputs and between input variables and the output are depicted (Fig. 1). From such results, it can be seen that the moisture content is highly correlated with the void ratio. The plastic limit, with a lower level of correlation, is in relatively strong relationships with the liquid limit and the void ratio. Otherwise, no direct relationship is found between the UCS and the input variables presented in the database.
3. METHODS USED
3.1. Random Forest (RF)
Random Forest (RF), a well-known supervised machine learning algorithm, is a nonparametric technique derived from classification and regression trees (CART), which applies ensemble learning method to solve problems [29]. Since the first introduction by Breiman [29], RF has been extremely applied in practice and with a wide range of applications, such as bioinformatics [30], materials sciences [31], remote sensing [32] or land cover classification [33]. RF is referred to construction of many trees, where each tree is generated by bootstrap samples. Then, a certain number of samples is kept for the validation process, which is called the out-of-bag predictions (OOB). Each split of the tree is constructed by a random process to create a subset of the predictors at each node. The final output of RF is the average of the results obtained by all the trees [29]. In this study, RF was applied to predict the UCS in which the number of bags used for bootstrapping was set at 500, whereas the optimal leaf size was set at 20.
3.2. Performance Assessment Criteria
In this study, various performance assessment criteria, namely Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Correlation Coefficient (R) were selected to evaluate the prediction capability of the proposed RF model. MAE, in general, is a statistical metric used for the assessment of the prediction quality of given soft computing algorithm [34], [35]. MAE measures the absolute difference between the predicted and experimental data. Besides, RMSE calculates the square root of the average of squared difference between the predicted and experimental data [36], [37]. R, the so-called Pearson correlation coefficient, is also a statistic measurement used to quantify the statistical relationship between the predicted and actual data [38]– [40]. The three criteria MAE, RMSE, and R are widely used in prediction problems utilizing machine learning algorithms. Literally, lower RMSE and MAE values mean better prediction capability. On the contrary, higher R values signify better performance [41]. The formulas of these criteria are given as below:
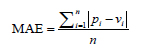 |
(1) |
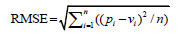 |
(2) |
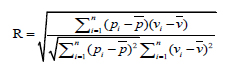 |
(3) |
where n is the number of data used, and are the ML predicted and mean ML predicted values, while and are the experimental and mean values of the UCS, respectively.
4. RESULTS AND DISCUSSION
4.1. Prediction Capability of RF
For UCS modeling and prediction, the RF algorithm was performed 20 times in randomly shuffling the training dataset (70% of the total samples) and the results of the best configuration was taken. The best adopted configuration was the one which gave highest value of R and lowest values of RMSE and MAE. The results and the corresponding values of error were presented.
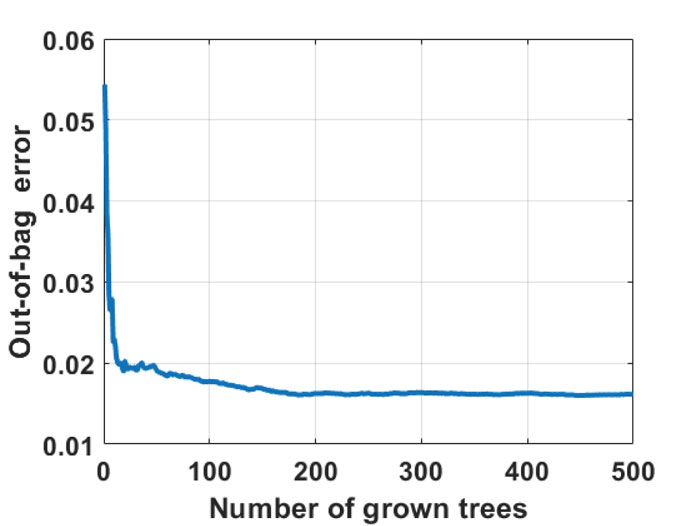
The out-of-bag regression error in predicting the soil UCS is shown in Fig. (2). It can be seen that the error stabilized from 200 grown trees, so that increasing the number of grown trees does not seem necessary. This indicated that such number was sufficient to obtain converged prediction results.
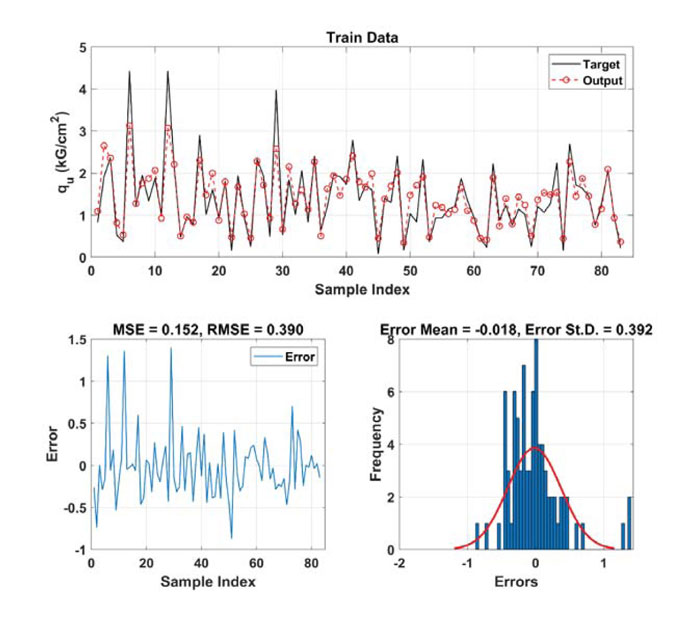
The validation process of RF algorithm was performed and shown in Fig. (3). For the training dataset, it can be clearly observed that the experimental data (continuous, black line) and the predicted UCS values (red circles, discontinuous line) obtained by RF model were in strong coherence. The maximum values of error between the predicted UCS were about 1 kG/cm2 for only 3 samples, whereas only 4 samples exhibited an error of about 0.5 kG/cm2. The values of MSE was 0.152, while RMSE value gave 0.390 kG/cm2. Out of these, smaller values of error were in the range around 0 and the probability density was rather narrow, with an average of -0.018 and a standard deviation of 0.392. It is thus universally concluded that RF method has an effectiveness in finding the optimal UCS solutions.
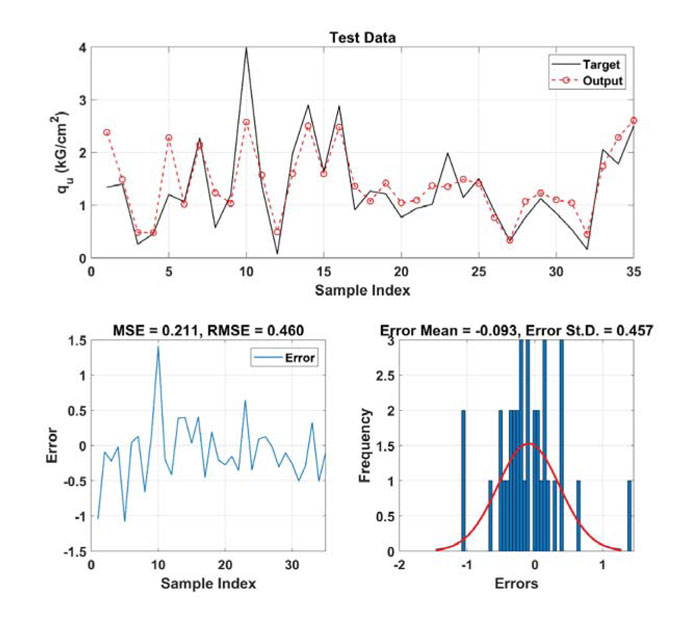
Regarding the testing dataset (30%), the predicted results using RF were highlighted in Fig. (4). It can be seen that, similar to the training part, the experimental data and the predicted UCS values were in good agreement. In this case, the maximum values of error were close to 1.5 kG/cm2 (only 1 samples), whereas only 3 samples exhibited an error of about 1 kG/cm2. The values of MSE for the testing dataset was 0.211 while RMSE value gave 0.460 kG/cm2. The values of error were centered on 0 with an average of -0.093 and a standard deviation of 0.457. The accuracy of the testing part was inferior to the training one, which helps preventing overfitting phenomenon.
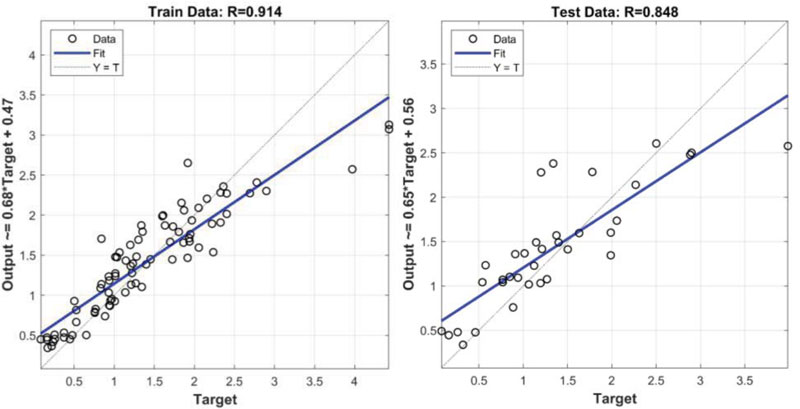
Validation results of the linear fit line, its equations and the R values are given in Fig. (5) for the training and testing datasets. The performance of RF in predicting the compressive strength values was satisfactory with R = 0.914, R=0.848 for the training and testing parts, respectively. Two linear fits were proposed and plotted in Fig. (5), where the slopes were computed as 0.68 and 0.65 for the training and testing datasets, respectively. The values of intercept were given as 0.47 and 0.56 for the two datasets.
This result demonstrates that the proposed RF model is suitable and can predict the soil compressive strength values which are, in general, close to experimental values.
4.2. Sensitivity Analysis
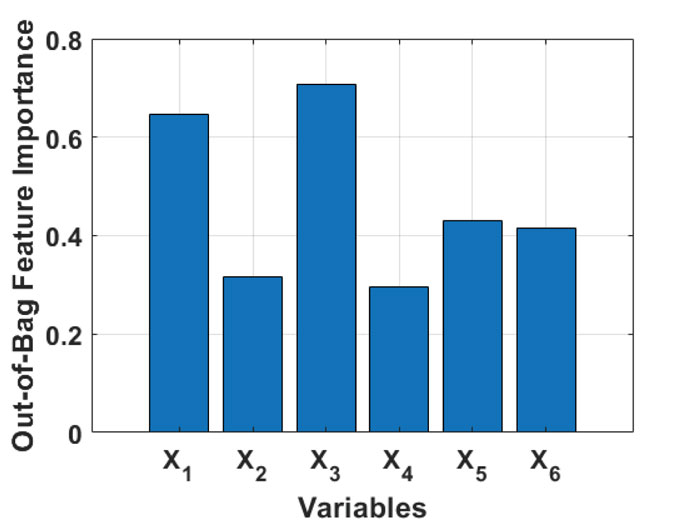
Naturally, the RF algorithm allows evaluating the significance of input parameters. The estimation of predictor importance values was conducted by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. Fig. (6) illustrates the out-of-bag feature importance of variables used in this study. It can be seen that the specific gravity (X3) is the most important variable in predicting the soil UCS as this factor is related to the density of particles presenting in soil [42]. Besides, the clay content (X1) is the second important input parameter, followed by the liquid limit (X5), plastic limit (X6) with equally importance, and the moisture content (X2), void ratio (X4), also with similar level of importance.
CONCLUSION
The soil unconfined compressive strength represents one of the important mechanical properties in civil engineering. In this study, the possibility of using the Random Forest algorithm in predicting the unconfined compressive strength of soil was investigated. A dataset containing 118 samples was constructed, taking the clay content, moisture content, specific gravity, void ratio, liquid limit and plastic limit as input variables. The main objective of the study was to predict the soil unconfined compressive strength. The verification on the reliability of the results was firstly conducted through analysis between the numbers of trees versus the out-of-bag error. The RF prediction process was then conducted and it was found that RF was a good predictor with satisfactory results of R, RMSE and MAE as 0.848, 0.460 and 0.093, respectively. A sensitivity analysis was carried out in order to reveal the importance of each given input to the predicted UCS. The specific gravity was found as most influential feature to the UCS, followed by clay content, liquid limit, plastic limit, moisture content and void ratio.
Many interesting perspectives of this study can be envisioned: (i) collection of more data of the UCS as to cover a wider range of input and output variables, (ii) analysis of the robustness of the RF algorithm taking into account the random data splitting using Monte Carlo simulations [43], as it is well-known that the accuracy of any ML algorithm strongly depends on the construction of the training dataset; and (iii) applying other ML algorithm or hybrid techniques to improve the prediction performance.
NOMENCLATURES
| UCS | = Unconfined Compressive Strength |
| RF | = Random Forest |
| R | = Correlation Coefficient |
| RMSE | = Root Mean Square Error |
| MSE | = Root Mean Square Error |
| MAE | = Mean Absolute Error |
| CART | = Classification and Regression Trees |
| X1 | = Clay Content |
| X2 | = Moisture Content |
| X3 | = Specific Gravity |
| X4 | = Void Ratio |
| X5 | = Liquid Limit |
| X6 | = Plastic Limit |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 105.08-2019.03.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


