All published articles of this journal are available on ScienceDirect.
Numerical Modeling of Masonry-infilled RC Frame
Abstract
Background:
The behavior of masonry-infilled Reinforced Concrete (RC) frame structures during an earthquake, has attracted the attention of structural engineers since the 1950s. Experimental and numerical studies have been carried out to investigate the behavior of masonry-infilled RC frame under in-plane loading.
Objective:
This paper presents a numerical model of the behavior existing masonry-infilled RC frame that was studied experimentally at the University of Patra. The objective of the present study is to identify suitable numerical constitutive models for each component of the structural system in order to create a numerical tool to model the masonry infilled RC frames in-plane behavior by accounting the frame-infill separation.
Methods:
A 2D masonry-infilled RC frame was developed in DIANA Finite Element Analysis (FEA) software and an eigenvalue and nonlinear structural cyclic analyses were performed. It is a 2:3 scale three-story structure with non-seismic design and detailing, subjected to in-plane cyclic loading through displacement control analysis.
Results:
There is a good agreement between the numerical model and experimental results through a nonlinear cyclic analysis. It was found that the numerical model has the capability to predict the initial stiffness, the ultimate stiffness, the maximum shear-force capacity, cracking- patterns and the possible failure mode of masonry-infilled RC frame.
Conclusion:
Therefore, this model is a reliable model of the behavior of masonry-infilled RC frame under cyclic loading including the frame-infill separation (gap opening).
1. INTRODUCTION
Masonry-infilled RC frame structures are widely dispersed around the world. Earlier studies have shown that the in-plane strength and stiffness of the infill walls have an influence on the global behavior of a structure, subjected to seismic loads. The existence of infill walls in an RC frame can increase the strength, stiffness (relative to a simple frame) [1, 2] and the lateral capacity of the building [2-4], and it can introduce brittle shear failure mechanisms associated with the wall failure and wall frame interaction. The role of the infill walls in earthquake-resistant structures is considered as very important and prevents the collapse of the relatively flexible and weak RC frame [5, 6].
Fardis et al. [4] and Kappos et al. [7] presented the global picture of the seismic behavior of masonry-infilled RC frame by referring to the energy dissipated by each member of the structural system as a function of the considered earthquake intensity. They revealed that over 95% of the energy dissipation takes place in the infill wall. In addition, the lateral stiffness of masonry-infilled RC frame is depended by flexural stiffness of the columns, beams and masonry. In addition, the flexural stiffness of the floor joists is an essential parameter in the determination of the dynamic characteristic (lateral stiffness) old type building structures or building without linking beams [8]. The floor joists contribute to the lateral stiffness of the structure by restraining the rotation of the columns at the floor level [9]. This type of restraint has a considerable influence on the overall frame stiffness.
In order to obtain the specific damage level (vulnerability assessment) caused by an earthquake to a given building type, the collapse mechanisms and the structural typology [10] of masonry-infilled RC frame must be specified. The failure mechanism and the load resistance of a masonry-infilled RC frame depend on the strength and stiffness of the infill wall with respect to those bounding frame (columns and beams surround the masonry infill). It is known that masonry structures are vulnerable to both in-plane and out-of-plane movement under the action of lateral loads. The in-plane and out-of-plane behavior of masonry-infilled RC frame have been studied experimentally [11] and numerically [12]. The out-of-plane failures turn out to be more disastrous than the in-plane ones [13].
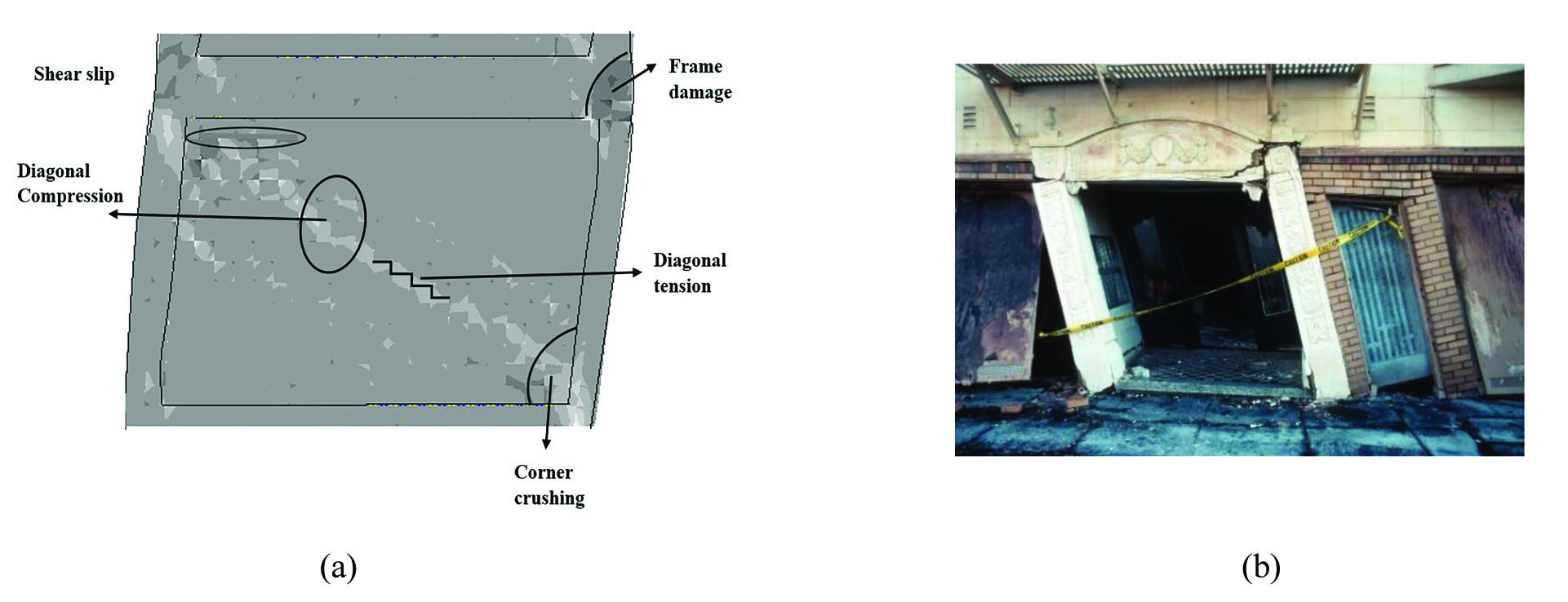
The in-plane failure mechanism of masonry structures is identified according to ATC 43 [14], Asteris et al. [15], Shing et al. [16] and Chrysostomou [17]. The infill wall fails in various modes and most often involves a combination of bed joint sliding, comer crushing, diagonal cracking (due to the diagonal orientation of the tensile-compressive principal stress), diagonal compression [17] and frame failure modes. The mode of failure of masonry-infilled RC frame depends on the material properties, such as compressive strength, shear strength and friction and on the geometry constraints, such as a frame-wall interface or window openings. Infill wall may have window and door openings. The existence of openings led to lower initial stiffness but more ductile behavior compared to masonry structure without openings [18, 19]. In the case of the infill wall with openings, the crack patterns are affected by openings. Fig. (1a) [20] shows the possible in-plane failure mechanisms of masonry-infilled RC frames.
In addition, the infill wall restrained by the bounding frame can develop out-of-plane resistance due to the developing of arching mechanism [21] and developed a bending out-of-plane failure that limits the strength of the wall, with respect to the previous failure mode. Such behaviors can be induced by different phenomena, such as ineffective connections between continuing walls, insufficient anchoring of the floors or out-of-plane horizontal loadings due to floors and roofs [11-13].
The infill wall influences the behavior of masonry structures as observed from the damages after recent earthquakes. The infill walls in RC structures cause several undesirable failure mechanisms under seismic loading due to the large concertation ductility demand in a few members of the structure. For instance, the soft-story mechanism (the interstory demand is in the first story) [22, 10], the short-column mechanisms (ductility demands on RC columns) [23], and plan-torsion mechanisms (infills are unsymmetrically located in the plan). In addition, the vertical irregularities introduced by the infill panels increase the seismic vulnerability of gravity-load design building [22]. The existence of the infill wall causes a shear failure of the columns, due to the increase in the stresses at the interface between the infill wall and frame [24].
The purpose of this paper is to simulate the behaviour of masonry-infilled RC frame under in-plane cyclic loading. To achieve this, 2D masonry-infilled RC frame model was developed in DIANA Finite Element Analysis (FEA) software, using meso-level approach for modeling the infill wall, and an eigenvalue and nonlinear structural cyclic analysis were performed. The present study identifies suitable numerical constitutive models of each component of the structural system in order to create a numerical tool to model the masonry-infilled RC frame behaviour by accounting the frame-infill separation. The calibration was based on the experimental test performed by Koutas et al. [25] for his Ph.D. study at the University of Patras.
2. MACRO-MICRO-MESO- MODELING OF MASONRY INFILL
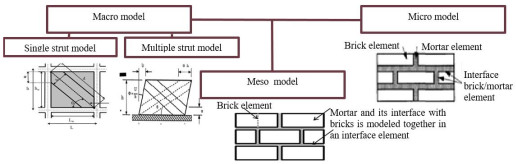
In the literature, different techniques that simulate the behavior of the infill wall can be found. The techniques are divided into three categories, namely micro-modeling, meso-modeling and macro-modeling [26, 27]. In micro-modeling, the wall panel is divided into numerous elements, considering the local effects in detail. On the other hand, macro-models are simplified models based on the psychical behavior of the infill wall [28]. In these models, the infill wall is replaced by the equivalent strut member along the loading direction. For large structure, it is better to use meso-modeling, which is between micro and macro-modeling approach. The most important factors for simulating the non-linear behavior of masonry-infilled frame arise from the material non-linearity (infill wall, frame and frame-infill interface) [29]. This study employs the meso-modeling approach to model the masonry infill. Fig. (2) presents the three modeling strategies for masonry infill.
2.1. Macro-modeling
The most popular method for modeling the masonry infill is based on the concept of replacing the infill wall with equivalent diagonal strut [30-36]. Although the fact that the single-strut model constitutes a sufficient tool for the prediction of the nonlinear response [32], the multi-strut model is superior in precision [30] [31]. In all strut models, the nonlinear strut behavior is described by constitutive monotonic or cyclic law [37]. In the case of multiple strut configurations [38], the assessment of a constitutive monotonic or cyclic law is needed for each strut. The representation of the non-linear cyclic behavior of masonry-infill with equivalent diagonal strut increases not only the complexity but also the uncertainties of the problem.
2.2. Micro-modeling
The micro-modeling approach considers the effect of the mortar joints as a discrete element in the model. According to Lourenco [39] and Asteris [40], in micro-modeling, the bricks units and the mortar are represented by continuum elements and the brick units-mortar interaction is represented by different interface elements, which leads to accurate results and intensive computational requirement [32]. Vertical interfaces can be introduced in the middle of the brick to reproduce its possible tensile failure. Past studies have investigated the use of a smeared crack approach for modeling the brick and mortar (quasi-brittle materials) [41-43] that leads to accurate results. An interface failure criterion for interface characterized by a tension cut-off, Coulomb friction law, and a compression gap model was developed [26]. The infill-frame contact is also modelled with the interface elements.
2.3. Meso-modeling
The main problem with micro-scale analysis is the significant computational demand that will be required to model large-scale structure. Therefore, for large structures, it is more reasonable to use meso-model. For the meso-modeling approach, the same element types, material properties and constitutive models are used as with the micro-modeling approach as described before. The exception that occurs in meso-model compared to micro-model is: the mortar is not explicitly modeled and the approach for modeling the mortar-brick interfaces differs as described here. In this approach, bricks are modeled by continuum elements, but the mortar joint and its interface with bricks are modeled together in an interface element. In the meso-modeling approach, the material properties and the constitutive law of the interface elements are modified to incorporate those of the mortar and the brick mortar joints.
3. DESCRIPTION OF EXPERIMENTAL CASE STUDY
In the experimental case-study carried out by Koutas et al. [25], the effectiveness of seismic retrofitting of existing masonry-infilled RC frame with Textile Reinforced Mortar (TRM) was studied. It was a 2:3 scale three-story structure with non-seismic design and detailing subjected to in-plane cycling loading. Two masonry-infilled frames were designed and built with and without TRM. The scope of this design effort represented a full height internal bay of an existing non-ductile building built in southern Europe in the 1960s. In this part, detailed description of the experimental case study regarding the masonry-infilled RC frame without the strengthening material TRM is presented, since the main scope of the article is to propose a numerical model to represent the masonry-infilled RC frame in-plane behavior. Full details about the experimental case study can be found in Koutas et al. [25, 44].
3.1. Geometry of Masonry-infilled RC Frame
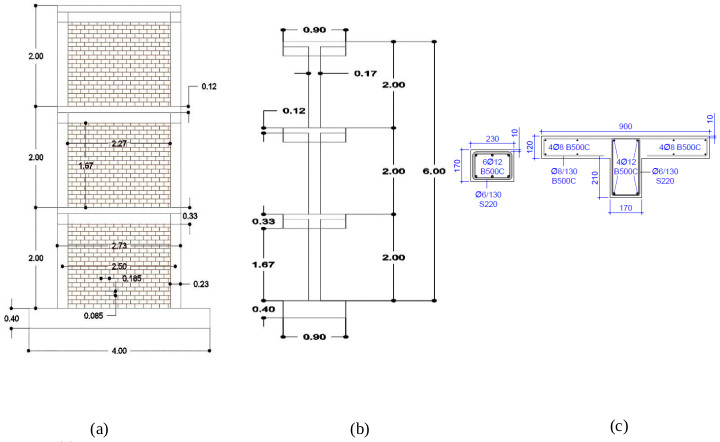
The geometry of the masonry-infilled RC frame is shown in Fig. (3). The scaled test specimens had a total height of 6.0 m (2.0 m per story) and a bay width of 2.73 m. The columns were of rectangular cross-section and the beams were T-section (Fig. 3c). The column deformed reinforcement was Y12 (longi tudinal) and lap-spliced only at the base of the first story. The transverse reinforcement for all concrete members was Y6 plain bars. The thickness of the concrete cover was 10mm. The dimension of the infill wall was 2.27x1.67x0.17m. The infill wall had a length-to-height aspect ratio of 1.36. The masonry wall was constructed from perforated, fired clay bricks (185x85x55mm). The perforation of the brick running parallel to the unit’s length in the x-direction. The infill wall was composed of two independent wythes separated by a gap equal to 60mm. Lime mortar was used between the bricks with a thickness of the bed and head mortar joint equal to 10mm. The wall was supported rigidly by the RC foundation beam plate with dimensions 0.4 x 0.9 x 4.0 m at the bottom of the frame.
3.2. Material Properties of Masonry-infilled RC Frame
For the construction of the RC frame, C25/30 class of concrete was used, with the compressive strength of concrete which was equal to 27.8 MPa for control structure. The modulus of elasticity of the concrete was 24.1 GPa. The reinforcement that was used is steel bars, class of B500C as longitudinal reinforcement in the beams and columns, and smooth steel stirrups class of S220. The mean value of yield stress was equal to 270MPa and 550 MPa for the smooth steel stirrups and for deformed reinforcement bar, respectively. Compression and diagonal test on masonry wall with dimensions of 500x500mm and thickness of 55 mm were performed. The mean value of compressive strength was 5.1 MPa and the modulus of elasticity perpendicular to the bed joints was 3.37GPa.The diagonal compression tests on masonry wallets were performed in order to determine the cracking strength and the shear modulus of the masonry wall. The mean value of diagonal cracking stress was 0.39 MPa and the shear modulus was 1.38 GPa.
3.3. Experimental Campaign
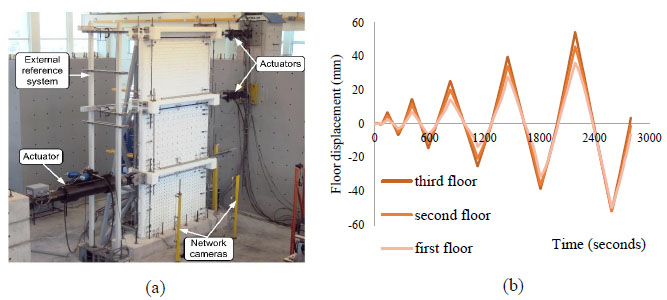
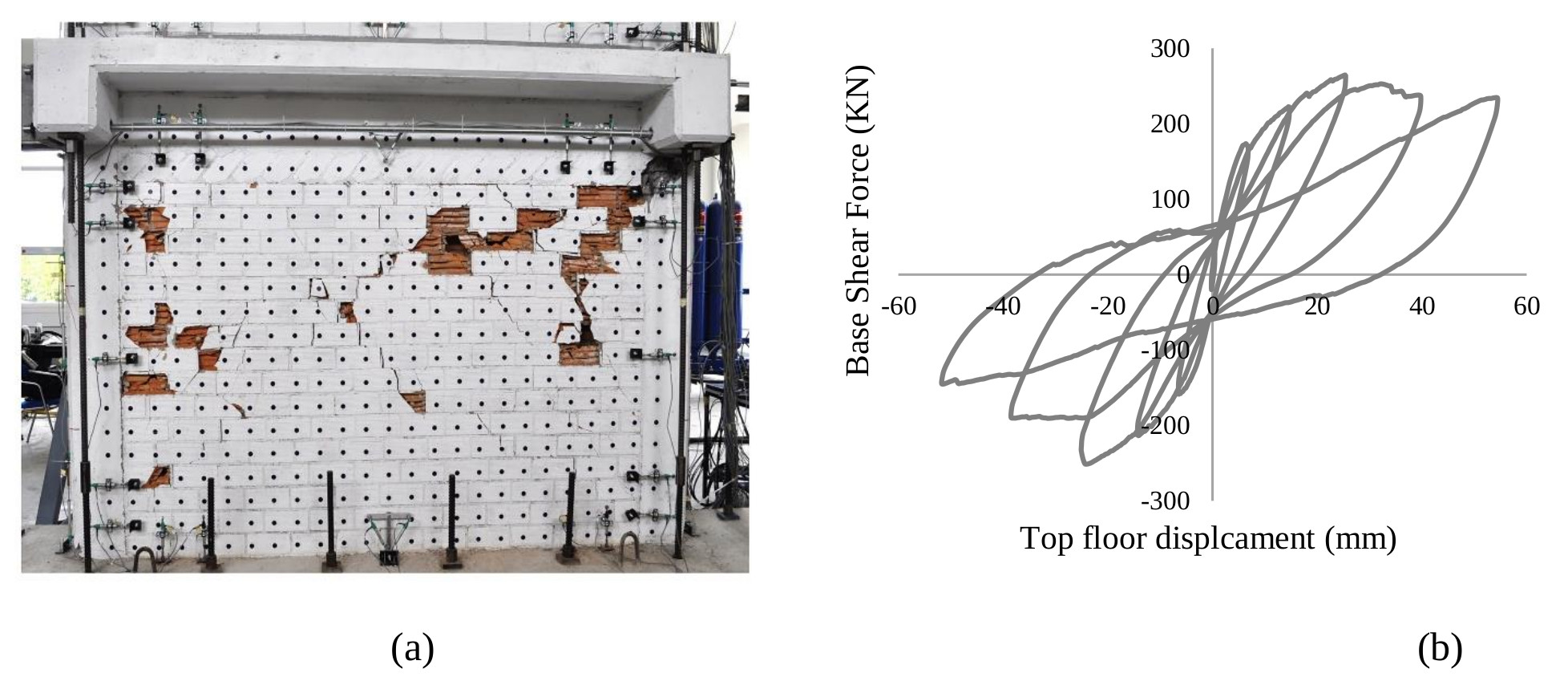
The masonry-infilled RC frame without TRM was loaded to a sequence of quasi-static cycles of a predefined force pattern. At the top floor, a history of cycles of displacement was applied as shown in Fig. (4b). At the same time, an inverted triangular distribution of forces, in terms of the global response, to all three levels, were kept until the failure occurred. Five cycles of loading were finally applied to the masonry-infilled RC frame without TRM. Fig. (4a) shows the test setup. In each floor level, a servohydraulic actuator was mounted on the structure as shown in Fig. (4a). In order to provide full clamping of the specimen with a laboratory floor, 16 prestressing robs were used on the foundation beam of the specimen. The gravity load with the value of 80kN per story was considered in order to represent the fraction permanent loads concurrent to lateral loading actions.
3.4. Experimental Results
Free vibration test was conducted in masonry-infilled RC frame to identify the experimental fundamental period of the structure in each phase of the construction. In order to perform the free vibration test, the specimens subjected to a static displacement at the top of the specimen. The gravity loading of 80 kN per story was not considered for the free vibration test. Table 1 shows the results of the free vibration test.
| Dynamic Characteristic | Bare Frame | Masonry-infilled RC Frame |
|---|---|---|
| Fundamental period (Seconds) |
0.24 | 0.06 |
During early loading in masonry-infilled RC frame,the cracking pattern was developed with step-type cracks parallel with the diagonal at the first story. Horizontal sliding-type cracking was also developed. During the last cycle of loading, the cracking pattern was completed. The cracking pattern that was developed includes two sliding cracks, one on top of the wall and the other at the mid-height of the wall that joined the tips of the step-type cracks of the previous cycle. Fig. (5a) shows the damage in the masonry infill in the first story at the end of the fifth loading cycle. Fig. (5b) shows the base shear force versus displacement at the top story. From the experimental results, the maximum base shear force was attained during the third cycle of loading. The maximum base shear was 264kN and -252kN for loading and unloading direction, respectively. The maximum top floor displacement was 25mm and -24mm for loading and unloading direction, respectively.
In addition, during early loading in masonry-infilled RC frame, the frame-infill wall separation has occurred. The interface between the columns and the infill wall exhibited large gap opening. The maximum gap opening was 2.0 mm for the first story(column-infill wall interface), 1.5mm for the second story (bottom slab-infill wall interface) and 0.7mm for the third story (bottom slab-infill wall interface).
4. FINITE ELEMENT MODELING OF MASONRY-INFILLED RC FRAME
This study used DIANA FEA software to model the masonry-infilled RC frame. The proposed meso –model for masonry-infilled RC frame was implemented in DIANA FEA using available materials, sections and elements. Two types of analysis were performed: Eigenvalue analysis and nonlinear structural cyclic analysis. The DIANA FEA was selected for the analysis since it provided the elements, constitutive relationships and materials needed for concrete, reinforcement and masonry infill [45].
4.1. Constitutive Model
In DIANA FEA software, there are different available material models to simulate the masonry-infilled RC frame. In this study, most of the material properties are taken from an experimental case study described above and other material properties are taken from the literature [43, 46, 47]. The numerical results were compared to the experimental results and some parameters were adjusted to achieve reasonable results.
The concrete material model that was chosen is the Total Strain Crack model [48]. The Total Strain-based Crack model describes the tensile and compressive behavior of concrete without taking into account the stress confinement effects, as shown in Fig. (6). In this model, the hypothesis of linear tension softening is considered to describe the tension stif fening effect although this model has uncertainties to capture the tensile behavior of concrete. A partial safety factor for the resistance model uncertainties for modeling must be considered equal to 1.15 [49]. Besides the definition of basic properties like Young’s modulus, the Total Strain Crack model requires an only small number of engineering parameters such as the tensile (2.15MPa) and compressive strength based on the Maekawa Fukuura model [50] (27.2 MPa) and the fracture energy in tension (130N/m). This model has no ability to reduce the stiffness due to early cracking of the concrete section and therefore the modulus of elasticity (9.1 GPa) was reduced. In addition, the tensile strength and fracture energy were obtained from the empirical equations 5.1-3a and 5.1-9, respectively according to the fib model code [46]. In this study, the approach which is used is the Rotating crack model [51] which is one commonly used approach in which the stress-strain relations are evaluated in the principal directions of the strain vector.
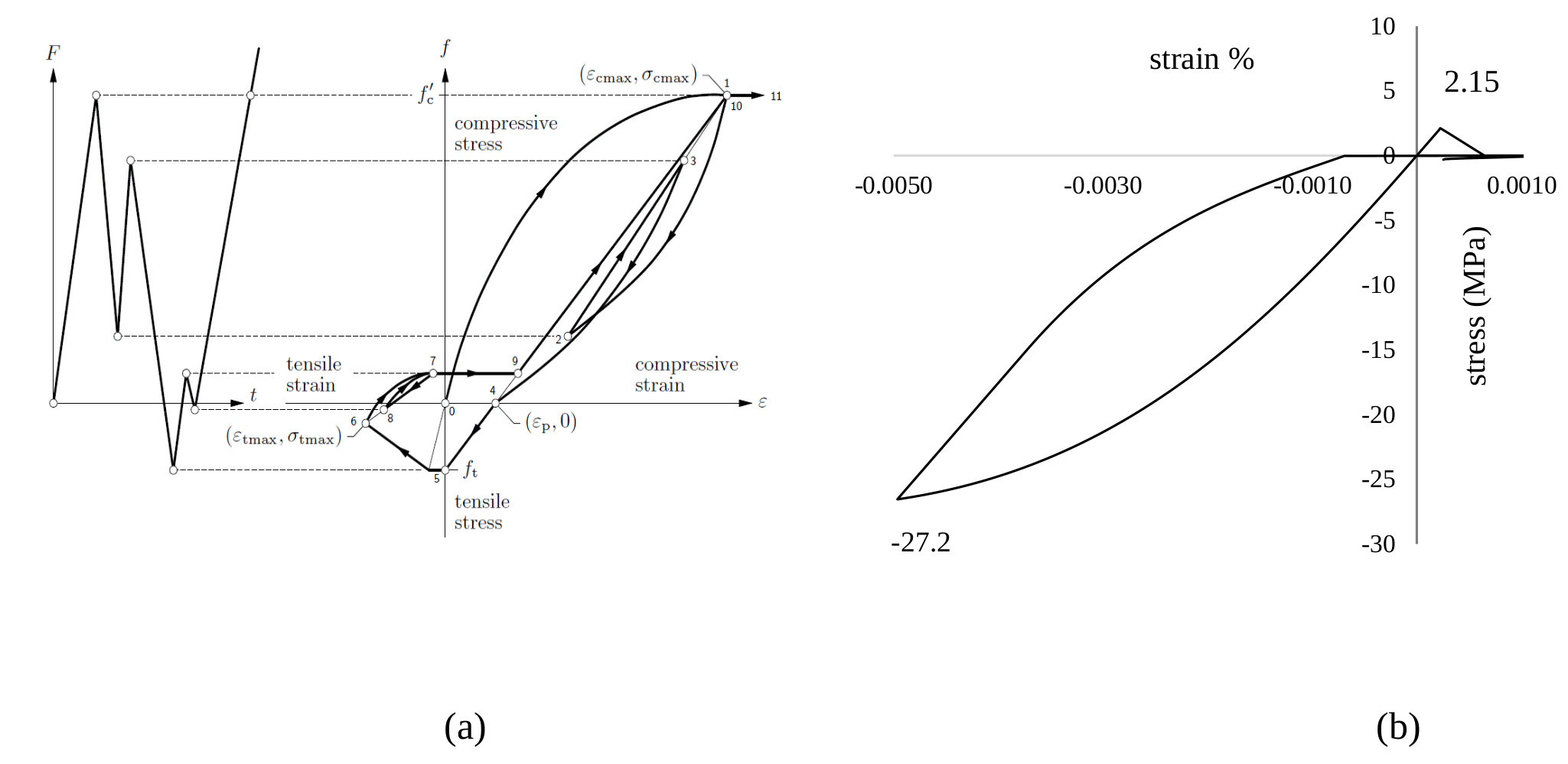
Cyclic performance of RC elements highly depends on the nonlinear response of reinforcing bars under cyclic loading. The Menegotto-Pinto model [50] is a special plasticity model for the cyclic behavior of steel reinforcement and it is available for embedded reinforcements. It consists of a finite stress-strain relationship for branches between two subsequent reversal points and the parameters involved are updated after each load reversal. The model is defined in DIANA FEA with the parameters as shown in Table 2.
The masonry infill material model that was chosen, is the Engineering Masonry model [53] which is a smeared failure model and it has a total-strain based continuum model that covers tensile, shear and compression failure modes. The Engineering Masonry model describes the unloading behaviour assuming linear unloading for compressive stresses with initial elastic stiffness. In addition, a shear failure mechanism based on the standard Coulomb friction failure criterion is involved in the Engineering Masonry model. The engineering masonry model requires a large number of engineering parameters and most of these parameters were not measured in the experimental case study. These material parameters were taken from the literature, as described below. The direct input parameters that are necessary to apply the Engineering masonry model as implemented in the DIANA FEA are shown in Table 3. The tensile strength normal to the bed joint was taken as 0.5 MPa [47] and the residual tensile strength was obtained 40% of tensile strength. The tensile strength of the joint is a subject of research and therefore, the tensile behavior parameters have been assumed according to the information provided by the respective experimental testing reports or related references. The compressive fracture energy and the tensile energy were calculated according to Rots [53]. The cohesion was obtained 1.5 times greater than that of the tensile strength according to the relation that was proposed by Cur [54]. The shear fracture energy was equal to ten times smaller of the cohesion as proposed by Lourenço [47]. The ratio between compressive and tensile strength which is often found for masonry units is about ten, so the friction coefficient is chosen according to this ratio.
| Elastic Parameters | |
|---|---|
| Modulus of elasticity (GPa) | 206 GPa |
| Initial yield stress (MPa) | Longitudinal bar: 549 Stirrups: 295 |
| Initial tangent slope | 0.05 |
| Initial curvature parameter (R0) | 20 |
The interaction between the frame and the masonry infill wall must be taken into account in the model since the interface between wall and frame influences the global response of masonry-infilled RC frame. In order to take into account this interaction, an interface gap model, plasticity based, proposed by Lourenco and Rots [55] was chosen. This model includes the Coulomb friction model for shear failure, the tension cut off criterion for the tensile behavior of the interface and the crushing to capture the compressive behavior of the gap model. Therefore, the fracture of the interface is controlled by tension, shear and crushing. There is one drawback regarding the use of this interface model, the lack of the engineering properties, as no data were available regarding the behavior of the interface between infill wall and frame. Therefore, it was decided to define the required properties of the interface model by fitting the numerical results to the experimental results obtained from the experimental case study. The engineering properties for the interface model are given in Table 4.
| Elastic Parameters | |
|---|---|
| Modulus of elasticity-X direction (GPa) | 7 |
| Modulus of elasticity-Y direction (GPa) | 3.37 |
| Shear modulus (GPa) | 1.38 |
| Mass density (Kg/m³) | 800 |
| Cracking: Head Joint Failure | |
| Tensile strength normal to the bed joint (MPa) | 0.5 |
| Residual tensile strength (MPa) | 0.2 |
| Fracture energy in tension (N/mm) | 0.05 |
| Crushing Parameters | |
| Compressive strength (MPa) | 5.1 |
| Fracture energy (N/mm) | 40 |
| Factor at maximum compressive stress | 4 |
| Compressive unloading factor | 0.2 |
| Shear Failure Parameters | |
| Cohesion (MPa) | 0.71 |
| Shear fracture energy (N/mm) | 1 |
| Friction angle (degree) | 20 |
| - | Y-direction | X-direction |
|---|---|---|
| Normal stiffness (kN /mm³) | 6 | 3 |
| Shear stiffness (kN /mm³) | 0.06 | 0.03 |
| Friction angle (degree) | 30 | 30 |
| Dilatancy angle (degree) | 0 | 0 |
4.2. Type of Elements and Mesh
DIANA FEA offers a broad range of element types for modeling brittle and quasi-brittle materials. The concrete frame and masonry infill wall were modelled with plane stress element and especially with eight-node quadrilateral isoperimetric plane stress elements (CQ16M). The steel reinforcement in the frame was modeled with two-node bar element and it is connected to the eight-node concrete element at the two external nodes. Fig. (7a) shows both elements.
The non linearity between masonry infill and RC frame zone was introduced with a 2D line interface element. The interface between the infill wall and the frame was modeled by the 3-point line interface element (CL12I) capable of modeling cohesion, separation, and cyclic behavior. The CL12I (Fig. 7b) element is an interface element between two lines in a two-dimensional configuration. The squared mesh is preferred in FE models [56] and therefore in this case study, the shape of the 2D elements was kept rectangular with nearly equal sides (Fig. 7c).
4.3. Type of Loading and Constraints
The model was loaded with a constant axial load (174kN/mm) on the top of each column (Fig. 7c) in order to simulate the dead load of the structure. In addition, the model was loaded with imposed cyclic horizontal displacement as shown in Fig. (5a). The loading process during the numerical analysis simulated as closely as possible to the experimental loading by using point prescribed deformation load. In order to model the strong foundation beam that was used in the experimental case study, all nodes at the base of the model were restrained by preventing any translation in the x and y-direction. Fig. (7c) shows the generated mesh, loads and the supports of masonry-infilled RC frame model.

4.4. Type of Analysis and Convergence
Two types of analysis were performed: eigenvalue analysis and nonlinear structural cyclic analysis (deformation control). To perform nonlinear cyclic analysis, two-phased analysis is selected. In the first phase, the self-weight and the additional dead load of the structure were imposed. In the second phase, a quasi-static implicit, material non-linear analysis was performed with the secant iteration scheme. The automatic incrementation procedure is used in which both the number of steps and the corresponding step size are automatically computed. The energy-based convergence criterion is applied with standard DIANA FEA tolerance values (0.0001). The continuation option was activated. The numerical model was calibrated to the experimental results by varying the parameters of the engineering masonry model and of the interface model.
5. FINITE ELEMENT MODEL RESULTS
In this part of the paper, the results of the eigenvalue analysis and nonlinear structural cyclic are presented. The fundamental period of the bare frame and for the masonry-infilled RC frame model is presented in Table 5 and they are in good agreement with the experimental ones.
The total mass of the bare and masonry-infilled RC frame was verified through the structural linear analysis. The structural linear analysis was performed for masonry-infilled frame model with and without interface element in order to verify that the stiffness parameters are successfully defined in the Coulomb-Friction interface model since the stresses and the strains remain the same regardless of the interface presence.
| Fundamental period(seconds) | Bare Frame | Masonry-infilled RC Frame |
|---|---|---|
| Experiment | 0.24 | 0.06 |
| Model | 0.23 | 0.062 |
The global results obtained from masonry-infilled RC frame model, subjected to cyclic loading, are shown in Fig. (8) which illustrates the experimental (black line) and numerical model (red line) response curves for the masonry-infilled RC frame. In addition, the base shear in relation to the load step and the top story displacement versus load step is presented in Figs. (8b and c) respectively.
A comparison between numerical and experimental results for masonry-infilled RC frame is given in Figs. (9a and b) in terms of global lateral stiffness and hysteric energy respectively. As illustrated in Figs. (9a and b) the agreement between modeling and test results is satisfactory.
Numerical results and experimental data of the masonry-infilled RC frame have been compared (Figs. 8-9) and are in excellent agreement with the experimental ones regarding initial stiffness, ultimate stiffness, maximum shear force capacity and energy absorption in a cycle. Based on the results from Figs. (8c and 9b), the shear-force capacity and the energy absorption for the last cycle of unloading are 30% and 10%, respectively. The base shear at the loading direction is underestimated, about 5-15%, in comparison with experimental results. The overestimation of the base shear in the last cycle of loading might be depended on the nonlinearities introduced in the last cycle of loading. The global stiffness of the numerical model at the first and forth cycle of loading is overestimated (9%) in comparison to the experimental results Fig. (9a). On the other hand, global stiffness in the third cycle of loading is underestimated about 12% and the energy absorption in the third and last cycle of loading is underestimated too.
Fig. (10a) shows the cracking that occurred at the first floor during the third cycle of loading and unloading in the experimental case study and Fig. (10b) shows the crack width in the numerical model during the third cycle of loading and unloading. The crack width in the numerical model shows that the cracks have the same location as observed in the experiment.
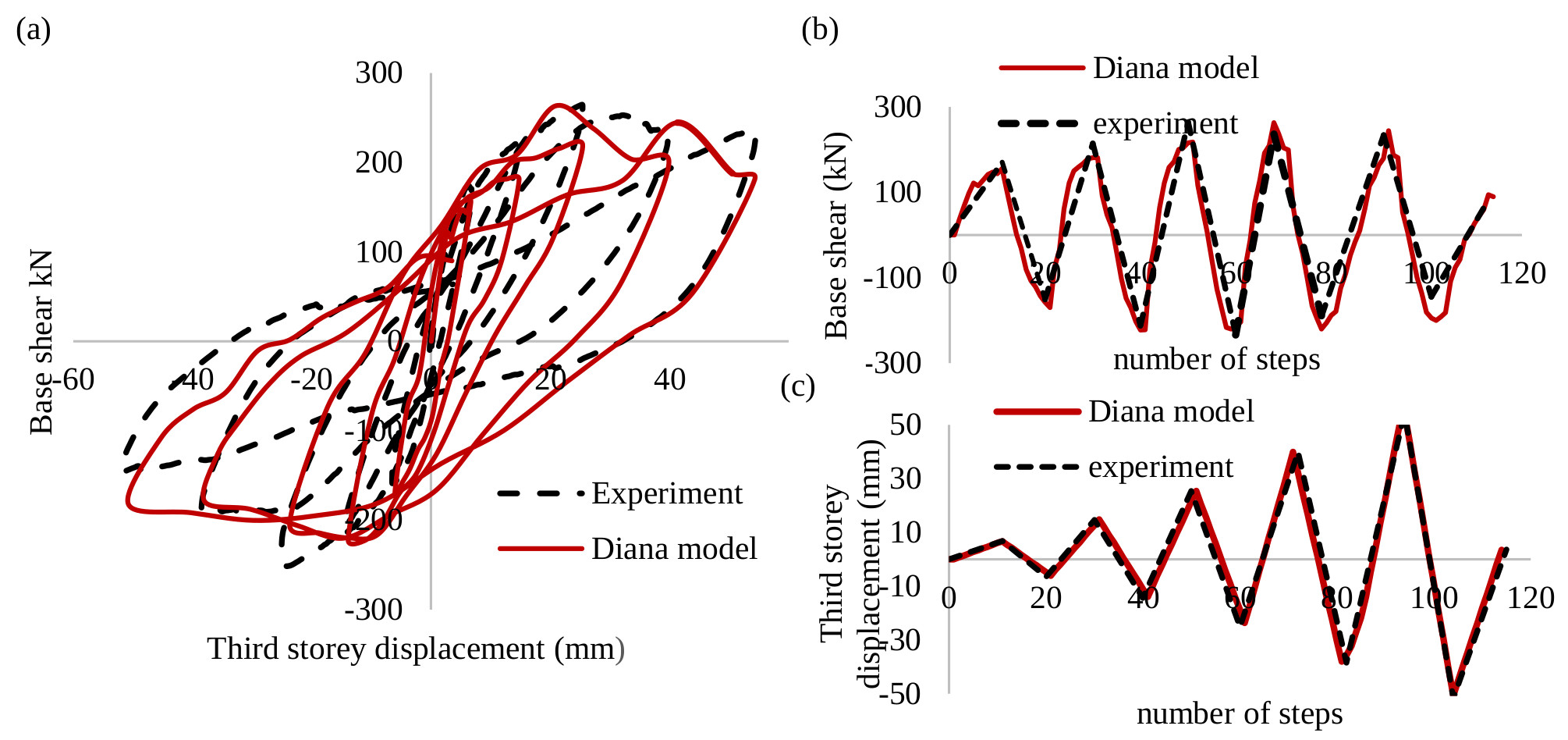
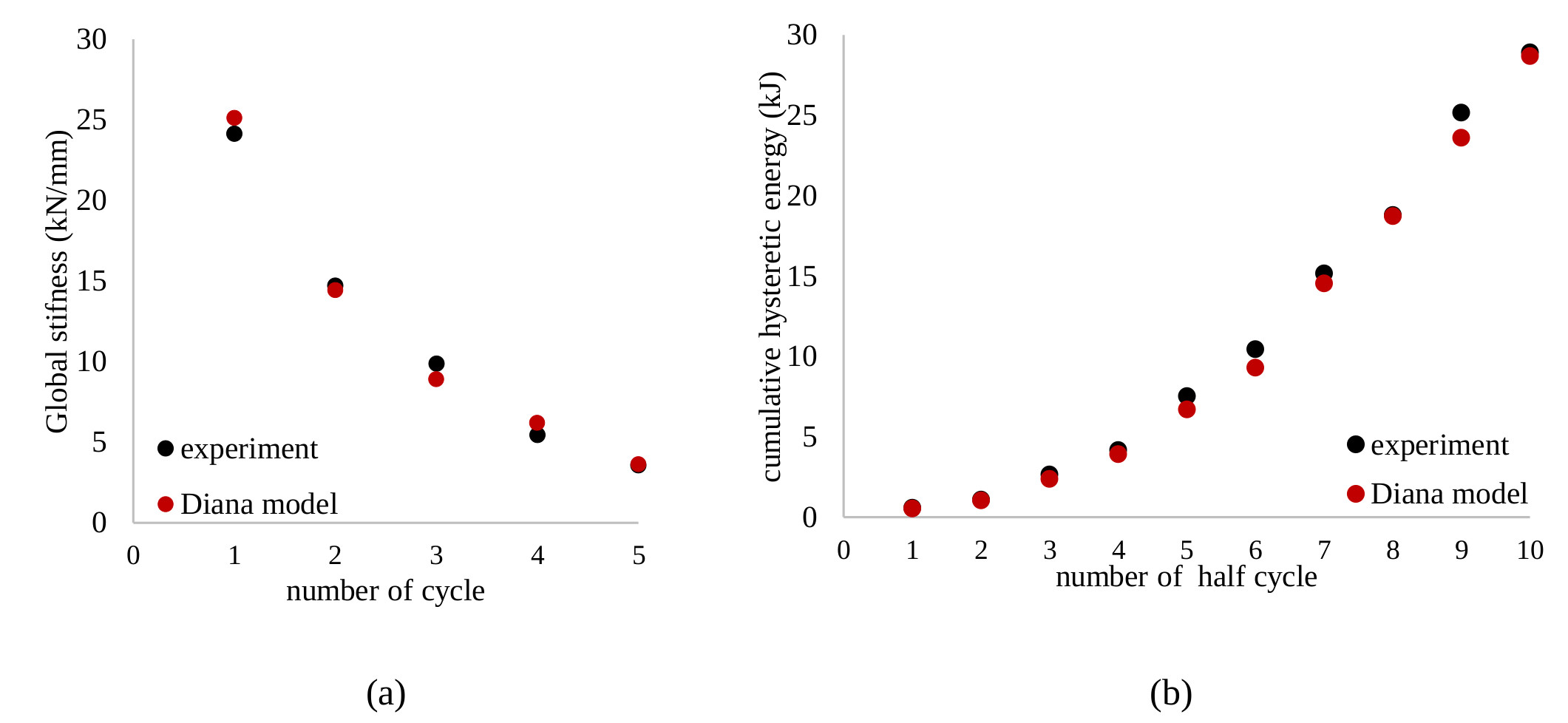
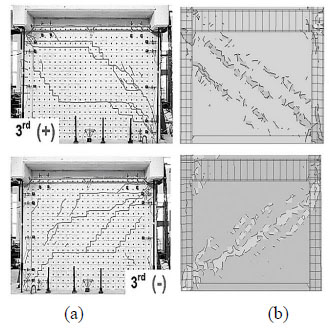

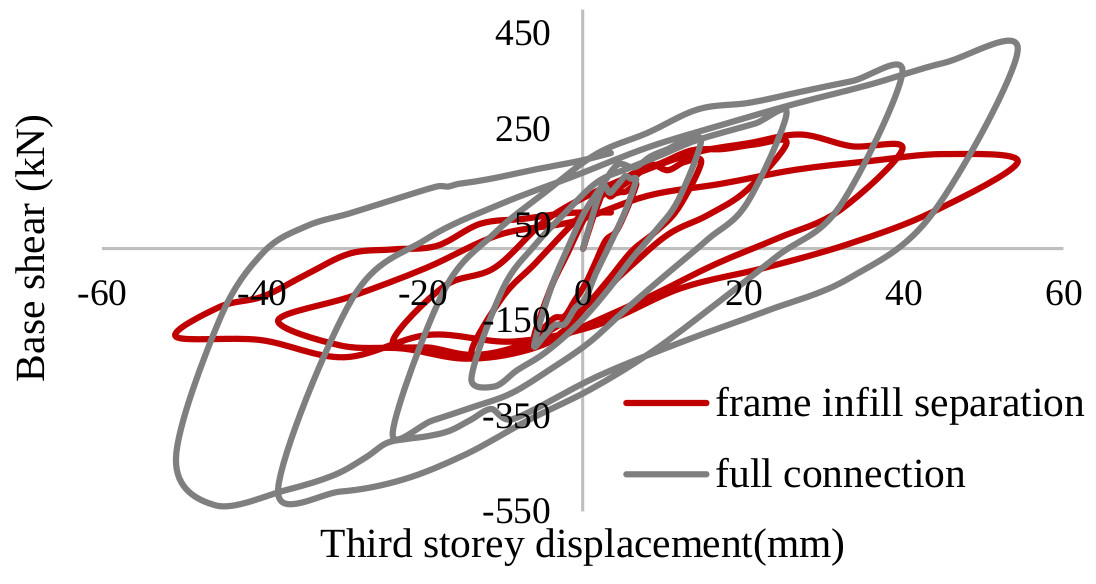
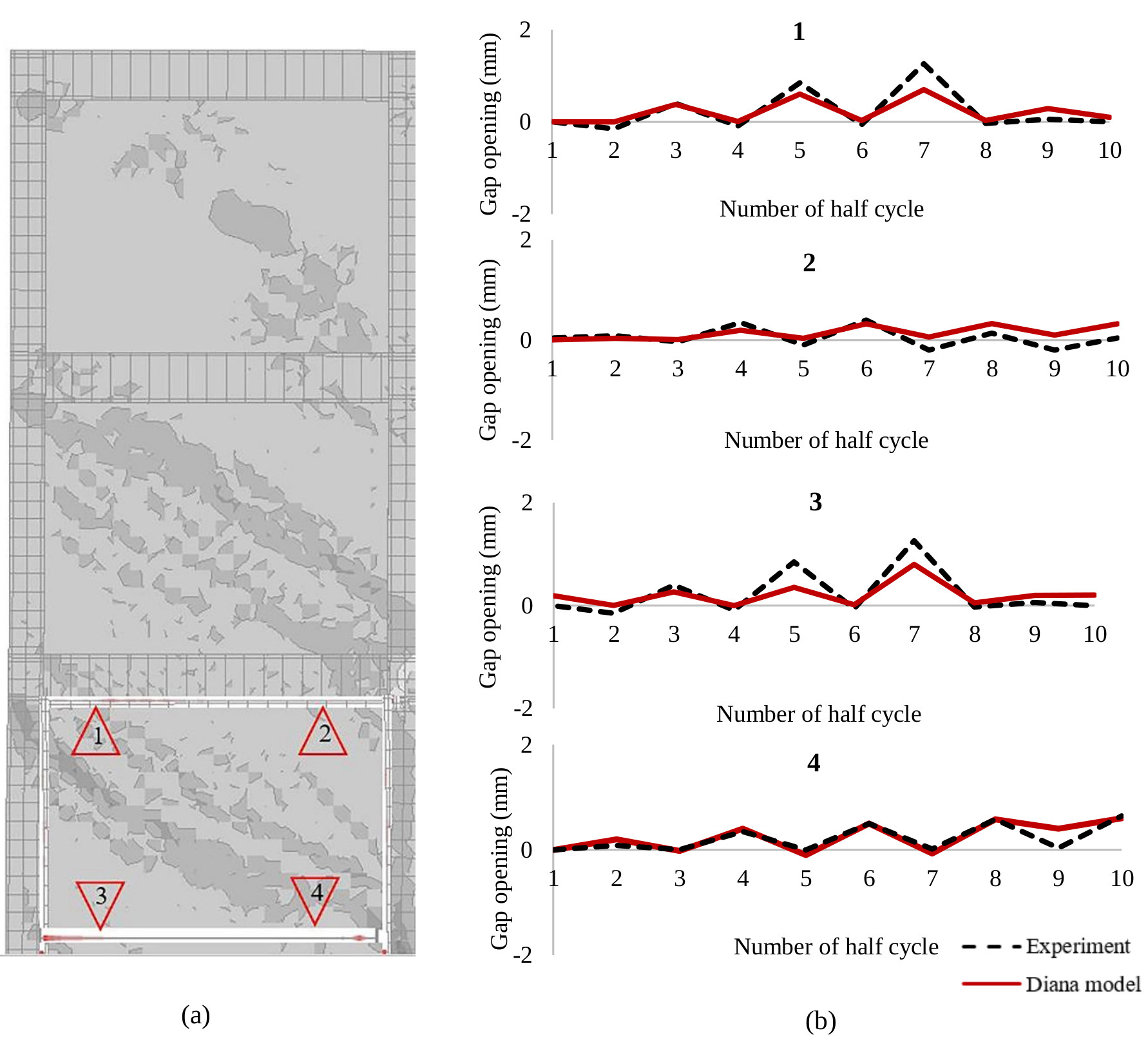
Fig. (10) verifies that the diagonal cracks of the masonry-infilled frame model occurred in the same location as observed in the experiment, therefore the specific failure mode at the infill wall was successfully captured in the numerical model. The results from the numerical model show the damage of the first story column (Fig. 11) which is the same damage that was observed in the experiment upon test completion.
Numerical results and experimental data of the masonry-infilled RC frame have been compared (Figs. 8-11) and are in excellent agreement with the experimental ones. In addition, the mismatch between numerical and experimental results is observed. The errors between numerical and experimental results that are calculated are due to the nonlinearities introduced in the last two cycle of loading. In addition, the simulation of masonry-infilled RC frame is complicated because this type of structure comprises of two interacting components of different material with different structural behavior and failure mechanism.
The complexity of the simulation of masonry-infilled RC frame also increases because, in the model, the interaction between the infill wall and frame must be taken into account. The behavior of the interface between infill wall and frame depends on infill wall-frame relative stiffness and wall-frame friction and bond strength. In order to capture the local interaction between the RC frame and infill wall, an accurate evaluation of the interface engineering properties is required. Fig. (12) shows the comparison of the results of the numerical model of a masonry-infilled RC frame including the infill wall-frame interface and with the full continuous connection between the frame and the infill wall, in terms of base shear versus top floor displacement.
From the analysis of the graph, it can be concluded that the introduction of an interface element (gap opening) is beneficial in comparison to the continuous connection between the frame and the wall. The introduction of the interface between the frame and the masonry significantly influences the overall behavior of the masonry-infilled RC frame. Therefore, more accurate simulation of masonry-infilled RC frame can be achieved by using interface element taking into account the interaction between the masonry and surrounding frame. The local results obtained from the masonry-infilled RC frame model are described in terms of the gap opening between the infill wall and RC frame. The infill-frame separation occurred at the very early stages of loading in the experiment and numerical model. Figs. (13a and b) show the shear stress distribution in the three stories of the model at third cycle of loading and the comparison between the experimental and model results for the gap opening of the interface on the first floor at four different positions (1-4).
The peak value of the gap opening between beams and infill on the first floor was 1.2mm in the experiment and 1.9mm in the numerical model. The maximum gap opening was 1.8 mm (column-infill) for the first story, 1.2 mm for the second story (bottom beam-infill wall) and 0.5mm for the third story (bottom beam-infill wall) which are the same gap openings that were observed in the experimental case study (Fig. 13b).
CONCLUSION
This paper presents a numerical model that stimulates the nonlinear cyclic behavior of masonry-infilled RC frame subjected to in-plane actions in DIANA FEA software. The simulation of masonry-infilled RC frame is a complicated problem in the engineering field because this type of the structure has two interacting components, one is the masonry wall and the other the RC frame, with different structure behavior and failure mechanism. In addition, in order to model the masonry-infilled RC frame behavior, the interaction between the infill wall and frame must be taken into account. The present study identifies suitable numerical constitutive models for each component of the structural system in order to create a numerical tool to model the masonry-infilled RC frame under in-plane loading. The calibration of the model was based on the experimental test performed by Koutas [25]. Some of the properties of the materials, especially for the masonry and for the interface were obtained from the literature [32, 50, 52],
Simulation results of masonry-infilled RC frame have been compared to the experiment ones with excellent agreement regarding the fundamental period, the ultimate stiffness and the maximum shear force capacity. Especially, the shear-force capacity of the model at the last cycle of loading is overestimated in comparison with experimental results and the global stiffness at the first and fourth cycle of loading is overestimated too. The introduction of the interface element between the infill wall and frame significantly influences the behavior of masonry-infilled RC frame. The gap opening between the infill wall and RC frame in the numerical model and in the experiment has been compared and presented an agreed correlation. The numerical model results have shown that the stiffness of the infill wall and therefore, the presence of the infill affect the fundamental period of RC structures. In addition, the lateral strength of masonry-infilled RC frame is higher compared to the bare frame. The crack-patterns show, in general, good agreement with the experiment with respect of orientation and location of the cracks.
It can be concluded that this model is a reliable model of the behavior of masonry-infilled RC frame, although acceptable mismatch between the test and simulation results is observed. In particular, the energy absorption and maximum shear-force capacity in the last cycle of loading are overestimated compared to the experimental results. In the future, this proposed numerical model which simulates the behavior of masonry-infilled RC frame will be used to perform numerical experiments through a parametric study to quantify the effect of critical parameters which are capable of affecting the performance of masonry-infilled RC frame. These results will contribute to the investigation of a general model for the application and the design of masonry infills in existing RC frame.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.