All published articles of this journal are available on ScienceDirect.
Designing Piled Foundations with a Full 3D Model
Abstract
Background:
The analysis of piled foundations, where horizontal environmental loads play a very important role, has taken foundation design a step further in the 1970s and 80s. Nonlinear analyses considering P-y, T-z and Q-z curves became the state-of-the-art which also included group effect calculations thanks to an approximation proposed by [1] on the [2] equations. For some reason, however, foundation design continued to be refined using finite element calculations, but the corresponding developments never made their way into the main offshore platform design codes such as [3,4].
Objective:
Considering the enormous advantage that this brings for topics such as group effect and negative friction, it is obvious that opening the offshore market to this enhancement is totally desirable. This is exactly what this paper is trying to achieve.
Method:
In order to increase the accuracy of the prediction of piled foundations lateral displacements when group effect is considerable, a complete 3D model will be proposed using the finite element method and compared to the codes’ model and also experimental data.
Results:
The model in DIANA showed good performance in comparison to the codes’ model and experimental data for the single pile. When the pile group model, when the codes’ have known deficiencies, was tested, both efforts on each pile and mean displacement of the pile group fit the experimental data. However, the behavior of each pile of the group, if separately analyzed, didn’t fit many experimental data, which was attributed to the soil model utilized.
Conclusion:
This improved modeling procedure has been proven to improve the lateral displacement prediction of a piled foundation when group effect is considerable, when compared to codes [3,4] proposed models. However, the study of more accurate soil models could help on achieving more realistic results.
1. BACKGROUND
The design of piled foundations was greatly enhanced during the 70s and 80s because of the need to cope with the large horizontal forces, which the environment produces on structures such as offshore fixed platforms, bridges, nuclear power plants and tall buildings.
While the offshore researchers made their developments based on a model considering a beam on elastic foundation and nonlinear soil resistance based on single dimensional soil curves, the power plant research was focusing on 3D nonlinear finite element soil models, into which the piles were embedded, thus producing a more accurate and general overall solution, whose development continued to be enhanced into the 21st century.
One would, therefore, expect this elegant enhanced solution to find its way also into the offshore market, but for some strange reason it failed to do so, wherefore it is fair to say that the present day offshore structure design codes deal with the design of piled foundations considering technology that became obsolete over the last 30 years.
It is also interesting to mention that while platforms, bridges, tall buildings and power plants all deal with group effect in the design of their piled foundations, only the platform codes have included a simplified method to calculate group effect (see a detailed description of this in [5]). All other structures deal with this problem more efficiently but the power plant designers are by far the most advanced. They take group effect into account automatically by modeling their piles embedded into a full 3D finite element mesh.
The object of this paper is to encourage offshore platform code and software developers to make use of the resources already available in the market, in order to perform more accurate analyses of fixed offshore platform piled foundations.
This is done first by discussing the modeling parameters of this new 3D model. This model was then used to simulate a full-size pile group test, which was performed in order to evaluate the horizontal interaction between the piles (known as group effect). This simulation was performed both using the full 3D model and again using the design procedure suggested in [3].
The software systems used to perform these analyses were the DNV-GL SESAM System for the typical offshore design procedure and the DIANA FEA Geotechnical Module for the 3D analysis.
2. METHOD
2.1. Pile and Soil Elements
The DIANA Geotechnical Module allows the user to consider one-dimensional pile elements embedded into a 3D mesh of solid soil elements, whose interface is modeled by the lateral bearing, axial skin friction and axial end bearing properties. The main advantage of this pile element is that its intermediate nodes are defined automatically by the program, based on the mesh defined for the soil. A pile joint is created for each soil element, which the pile intersects (Fig. 1).
The pile joints are connected to the soil elements by springs, which are tangential and normal to the pile axis.
The pile elements are space frame elements, which are continuously connected to the solid FE soil elements. The 3D soil elements can be tetrahedral, pentahedral or hexahedral, with joints at the vertices only, or with an additional joint along each of the edges, as shown in Fig. (1). These intermediate joints are, once again, important if nonlinear geometry or nonlinear soil behavior is to be considered.
Regarding the interaction properties acting in the tangential direction of the pile axis, there are two different types: one is the lateral friction and the other represents the end bearing. The latter is non-zero only at the pile tip or if there is a diameter transition. An interesting possibility here is to model these springs using the T-z and the Q-z functions already available in the codes or defined by the soil consultants. This would allow the axial bearing capacity given in the code curves to be fully considered, but one must be aware of the fact that the corresponding displacements will be added to those of the soil modeled by the solid elements. This means the curves would have to be adjusted. The other alternative would be to make them rigid, thus considering only the soil mesh displacements. The springs that represent the pile-soil interaction normal to the pile axis, could be treated the same way as above.
It is obvious that there is a great amount of research backing the P-y, T-z and Q-z curves given in API, DNV-GL, ISO and other codes and that the same amount of research is not yet available for the 3D FE soil elements. It would be interesting, therefore, to consider these interface springs as a transition phase from the present day model (beam on elastic foundation with nonlinear springs) to the enhanced 3D FE soil model with embedded piles. More will be said about this in the following section were the properties of the 3D FE soil elements are discussed.
2.2. Soil Constitutive Model
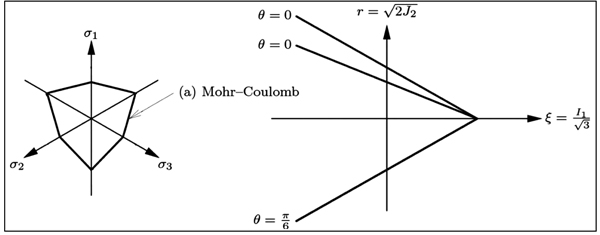
The Mohr-Coulomb flow condition (Fig. 2), shown on the left side in the plane and on the right side in the Rendulic plane, is an extension of the Tresca flow condition to a pressure dependent behavior. The formulation of the flow function can be expressed in the main stress space (σ1 <σ2 <σ3) as Eq. 1.
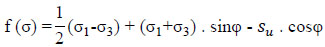 |
(Eq. 1) |
The plastic potential is given by a general law not associated (g ≠ f) flow rule, but with the plastic potential given by Eq. 2.
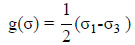 |
(Eq. 2) |
From the plastic potential we can obtain an expression for the vector of the rate of variation of plastic deformation as per Eq. 3.
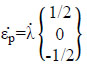 |
(Eq. 3) |
A more detailed theoretical background for this method may be found in the DIANA software manual.
3. EXPERIMENTAL DATA
The dissertation [6] carried out an experimental test with a group of 15 piles arranged in 5 rows, 1.27m (3.92 times the diameter D of the piles) apart from each other with 3 piles in each, as shown in Figs. (3 and 4). An additional single pile was driven alongside, sufficiently away to avoid any group effect, which was intended to help perform the corresponding measurements. All of the piles are 13.1m long.

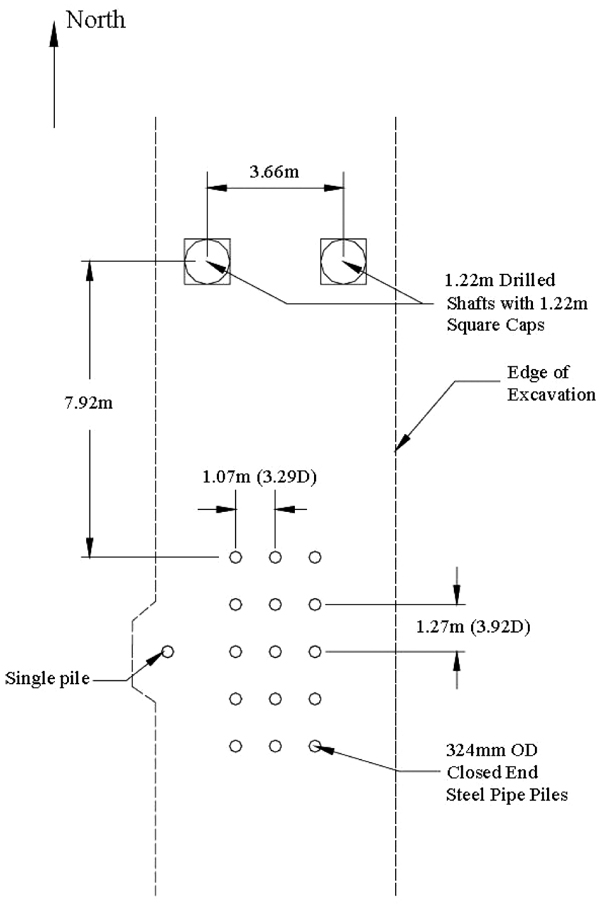
A steel truss rigidly interconnected all the 15 pile heads, so that they could all undergo the same pile head displacement, by reacting the truss against a much more rigid foundation. The connection of the truss to each of the piles was pinned so that they could rotate freely (Fig. 5).

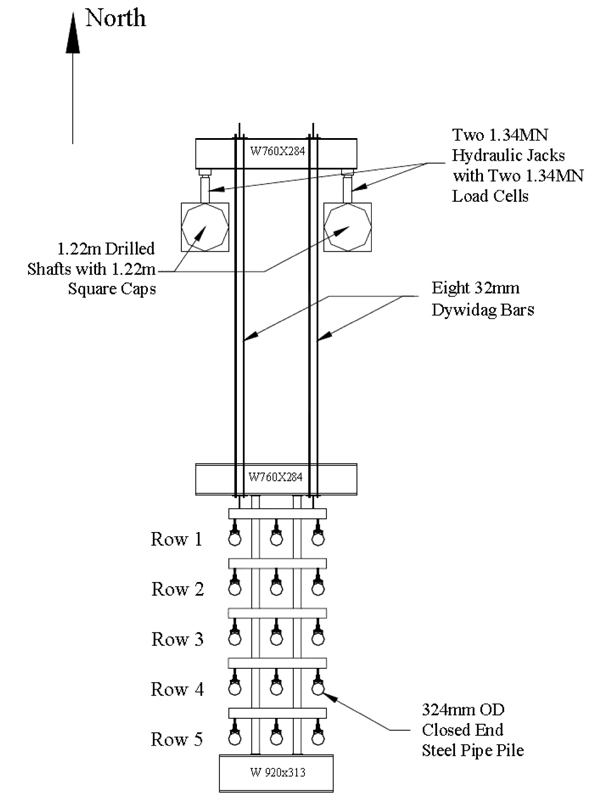
All of the piles were fabricated according to the ASTM A252 Grade 3 specifications. Their cross section was tubular with a 423mm outer diameter and 9.5mm wall thickness. The modulus of elasticity was 207 GPa. The bottom tip of the piles was closed.
The displacement of the rigid truss, which causes all pile heads to translate by the same value is introduced by two hydraulic jacks, which react against two much more rigid foundations, that have been installed just ahead of the pile group. The displacement of these rigid foundations is negligible, so the displacement of the pile heads is basically the same as the expansion of the jacks (Fig. 6).
Test measurements were performed using strain gages installed along the pile, protected by angles as indicated in Fig. (7). The strain values measured by these gages were used to determine the bending moments introduced by the top deflection of the system.
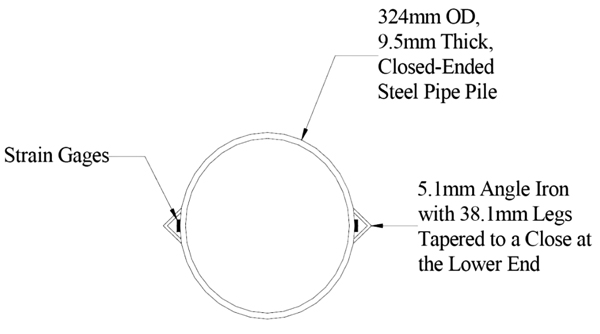
In addition to the strain gages used to measure the bending moments, potentiometers (with 0.25mm precision) and LVDTs (Linear Variable Differential Transformers - precision of 0.127mm) were used to measure the lateral pile head displacements.
Finally, in order to measure the applied load, load cells were installed at the connection of the steel truss with the two rigid foundations.
[6] 2005, had some problems measuring the bending moments because of some failures which occurred during the test. Initially, they had intended to move the heads of the piles progressively by 6, 13, 19, 25, 38, 51, 64 and 89mm. This would occur in a total interval of 5 days. Unfortunately, when the system reached the 51mm step, one of the load cells failed, twisting the pile head truss, wherefore it had to be unloaded and realigned. Unfortunately, the strain gage measurements were no longer trustworthy after this. Because of this, the bending moments are presented only up to 38mm deflections.
The dissertation thesis [7] performed some computational runs with a DNV-GL software called SPLICE, which is part of the SESAM system, in order to simulate the tests carried out by [6] 2005. SPLICE determines the pile displacements and forces based on the beam on elastic foundation model, with the soil modeled as P-y, T-z and Q-z curves. The group effect calculations are performed based on [1, 2]. [7] results will be presented ahead along with those developed in this paper.
[6]´s experiment was analyzed here considering a full 3D FE model as described above, in which the group effect is taken into account automatically. The software used was the DIANA Foundation Module. Graphs comparing the test results to simulations performed in SPLICE and DIANA are presented below.
The soil properties obtained from geotechnical tests presented by [6] that were used also by [7] are presented in Tables 1 and 2, which were used also here to generate the Mohr Coulomb data presented in Table 3.
| Parameter | Sand 1 | Sand 1 | Clay 2 | Clay 3 | Sand 2 | Clay 4 | Sand 3 |
|---|---|---|---|---|---|---|---|
| Depth [m] | 0 - 2.4 | 2.4 - 2.7 | 2.7 - 3.7 | 3.7 - 4.6 | 4.6 - 6.3 | 6.3 - 8.0 | 8.0 - 15.0 |
| γ [kN/m3] | 16.7 | 19.1 | 19.1 | 19.1 | 18.1 | 19.1 | 16.7 |
| su [kPa] | 0 | 41 | 50 | 40 | 0 | 57 | 0 |
| φ [degrees] | 40 | 0 | 0 | 0 | 38 | 0 | 33 |
| ε50 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| J | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| tcomp [kPa] | 38 | 41 | 50 | 40 | 29 | 57 | 23 |
| ttens [kPa] | 19 | 41 | 50 | 40 | 15 | 57 | 12 |
| tres/tmáx | 1.0 | 0.8 | 0.8 | 0.8 | 1.0 | 0.8 | 1.0 |
| ztres [mm] | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
| Qp [kPa] | 7660 | 372 | 450 | 360 | 5743 | 512 | 4599 |
| z/D | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 |
| Water level 2.13m below the surface | |||||||
| Parameter | Lateral Piles | Central Piles |
|---|---|---|
| γ [kN/m3] | 28 | 28 |
| Outside Diameter [mm] | 324 | 324 |
| Thickness [mm] | 9.5 | 9.5 |
| Yielding Stress [MPa] | 405 | 405 |
| Modulus of Elasticity [GPa] | 207 | 207 |
| EI [kNm2] | 29600 | 24010 |
| EA [MN] | 2104 | 1943 |
| Pile Tip Condition | Free | Free |
| Loads applied 0.483m above the soil surface | ||
| Depth [m] | Sand 1 |
Clay 1 |
Clay 2 |
Clay 3 |
Sand 2 |
Clay 4 |
Sand 3 |
|
|---|---|---|---|---|---|---|---|---|
| 0 - 2.4 | 2.4 - 2.7 | 2.7 - 3.7 | 3.7 - 4.6 | 4.6 - 6.3 | 6.3 - 8.0 | 8.0 - 15.0 | ||
| Linear Elasticity Data |
E [kPa] |
25000 - 55000 | ||||||
| ν | 0.3 | |||||||
| γ [kN/m3] |
16.7 | 19.1 | 19.1 | 19.1 | 18.1 | 19.1 | 16.7 | |
| Plasticy Data | su | 0 | 41 | 50 | 40 | 0 | 57 | 0 |
| φ | 40 | 0 | 0 | 0 | 38 | 0 | 33 | |
| Tensile Stress [kPa] |
0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Initial Stress | K0 | 0.6 | 1.0 | 1.0 | 1.0 | 0.6 | 1.0 | 0.6 |
| Water level 2.13m below the surface | ||||||||
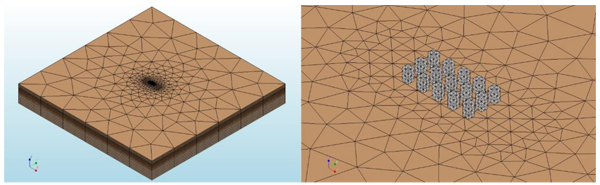
Having defined all the properties of the model, its geometry was defined making use of the DIANA modeling tools. The piles were modeled as unidimensional quadratic elements (space frame elements with an intermediate node) and the soil with tetrahedral and pentahedral elements all of which had nodes at the vertices only (Figs. 8 and 9). Please note that small pile caps were modeled at the top of each pile in order to apply prescribed displacements to them.
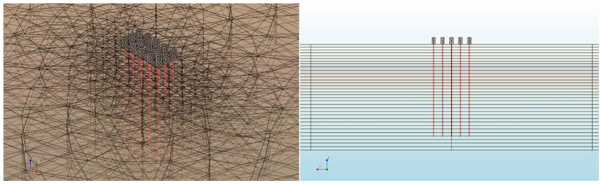
The load was applied progressively to the pile head truss by prescribed displacements in 1mm steps. The self-weight of both the soil and the piles was considered automatically by the program. These were considered first and only then were the external loads applied.
4. RESULTS
The measurement results of the experiments used to evaluate the calculation results were:
- The bending moment diagrams;
- The shear force diagrams;
- The pile top displacements.
Figs. (10-16) contain the [6] 2005 measured test results compared to those extracted from DIANA and those obtained by [7] using SPLICE.
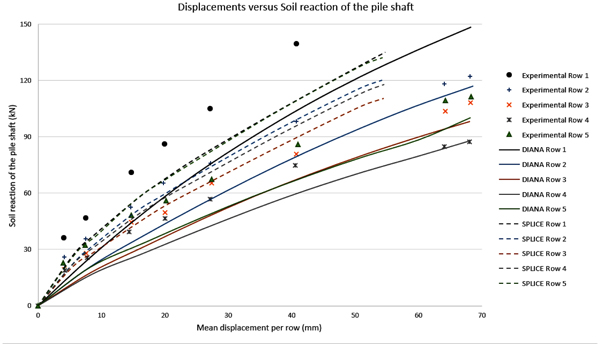
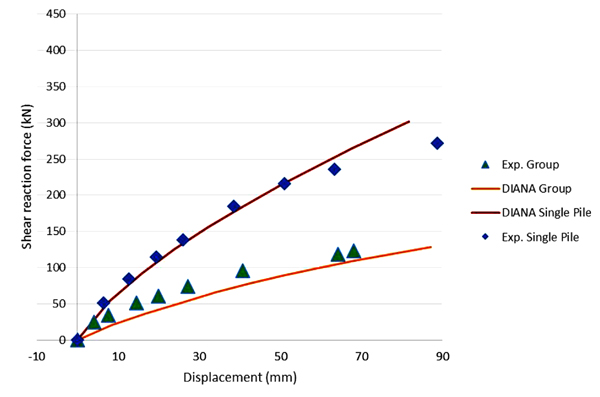
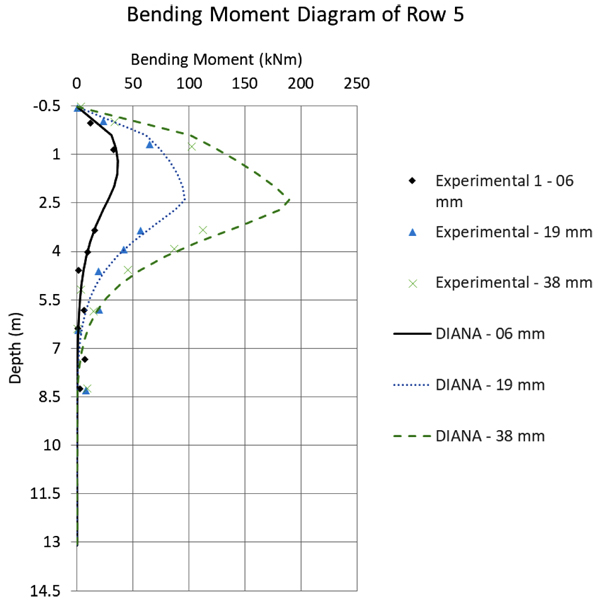
Fig. (12) to 16 compare the bending moment diagrams obtained in DIANA with the 3D model, with those measured by [6] 2005. It can be seen that once again the agreement is good. These comparisons were made on a row-to-row basis, which differ considerably because of the varying group effect. These results show also that DIANA predicts not only a good agreement for the average group effect, but also for variations from pile to pile.
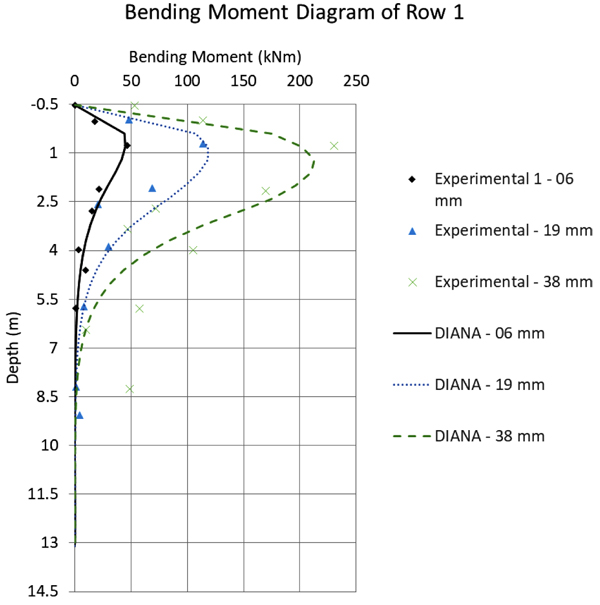
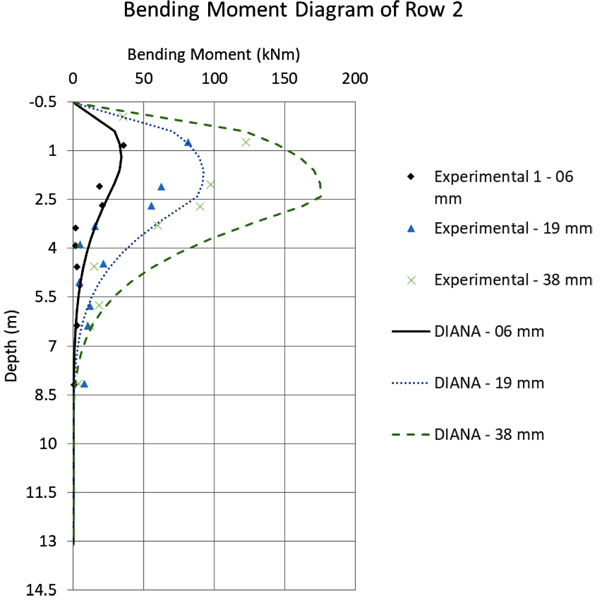
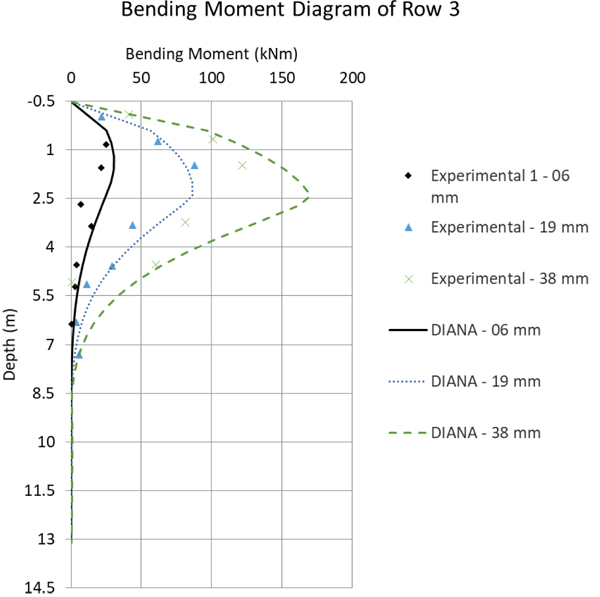
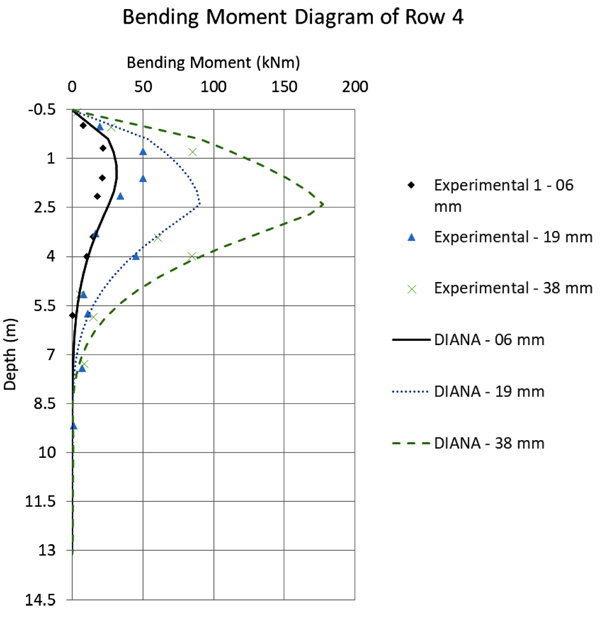
In general, one can observe in the comparative graphs presented in Fig. (10) that for rows 1, 2 and 3, DIANA shows good agreement with the SPLICE results, which are based on the beam model, the [3] soil curves and the simplified group effect method. However, the SPLICE results are a little closer to the experimental results with respect to displacements up to 40mm. The experimental results, in this case, tend to present a stiffer solution.
In the same Fig. (10), for rows 4 and 5 DIANA shows a very good prediction for larger displacements, while SPLICE results are worse. This happens because, for larger displacements, SPLICE fails to capture the plastic behavior of the soil. Still regarding the comparison between the DIANA model and the test results, one can observe that the initial DIANA lateral displacements are slightly smaller. This is attributed here to the Mohr-Coulomb theory that was used, which is perfectly-elastic-plastic. A more accurate soil theory could deliver even better results, for example considering a hardening soil model.
Fig. (11) presents two different DIANA curves and their comparison to the test results. The upper results show the pile head displacements of the single pile of the experimental study as a function of the pile shear force. In this case, the DIANA and the test results show an excellent match. The lower curve presents the lateral displacement of the steel truss connecting all the piles as a function of the total lateral force divided by 15 (number of piles). This time there is still a reasonably good match, but DIANA seems to tend to exaggerate the group effect.
CONCLUSION
The original intent of this contribution was to develop a procedure that could be similar to that proposed by [3, 4] for the evaluation of offshore piled foundations but based on the general 3D finite element methods, which could be applied to better evaluate lateral displacements in piled foundations. Unfortunately, the authors have found that the task was larger than originally anticipated, because the 3D soil models, available in the market, were found to be considerably less developed than the P-y, T-z and Q-z curves presented in these same codes.
The source of this contribution was, therefore, limited to finding a software with which the original [3, 4] soil curves could continue to be used, but within this new framework of the 3D Finite Element Method, which would handle group effect very efficiently.
Within this paper, therefore, soil properties, used in a Mohr-Coulomb approach, were investigated for the specific problem that was analyzed, but these do not cover all general soil types as initially desired. Nevertheless, using a software like DIANA, it is possible to immediately replace the beam solution presently recommended in [3, 4], without changing the code recommendations for the soil properties.
The test results, which were analyzed here [6], have confirmed the well-known fact that single piles can be analyzed with similarly good results both based on the full 3D Finite Element Method (analyses performed with DIANA) as the beam on elastic foundation theory (analyses performed with DNV-GL SPLICE, by [7]). When, however, group effect is added to the problem, the results produced by the latter are no longer so good.
NOTATION LIST
| P | = is the mobilized lateral resistance, unit of pressure; |
| y | = is the local pile lateral displacement; |
| T | = is the mobilized soil-pile axial friction; |
| Q | = is the mobilized end bearing capacity, in force units; |
| D | = diameter |
| OD | = outside diameter |
| γ | = unit weight of soil |
| su | = undrained shear strength of the soil at the point in question, in stress units |
| φ | = angle of internal friction of sand, for drained triaxial conditions |
| ε50 | = is the strain at one-half the maximum deviator stress in laboratory undrained compression tests of undisturbed soil samples |
| J | = is the dimensionless empirical constant with values ranging from 0.25 to 0.5 having been determined by field testing |
| tcomp | = skin friction when the pile is subjected to a compressive force |
| ttens | = skin friction when the pile is subjected to a tensile (pullout) force |
| tres/ tmax | = ratio of residual soil-pile adhesion or unit shaft friction to maximum soil-pile adhesion or unit shaft friction at depth z, for axial shear= transfer t-z curves |
| z | = depth below the original seafloor, local pile axial deflection, for axial shear transfer t-z curves and axial pile tip displacement, for q-z curves |
| ztres | = axial pile displacement at which the residual soil-pile adhesion, tres, is reached |
| Qp | = end bearing capacity, in force units |
| z/D | = ratio between the z of peak stress resistance and the outside diameter D of the pile |
| EI | = product of elastic modulus and sectional inertia |
| EA | = product of elastic modulus and sectional area |
| E | = elasticity modulus |
| ν | = Poisson’s ratio |
| K0 | = coefficient of lateral earth pressure at rest |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


