All published articles of this journal are available on ScienceDirect.
Equivalent Non-Linearization of Hysteretic Systems by Means of RPS
Abstract
Background
The analysis of elastoplastic systems with hardening (Bouc-Wen systems) under stochastic (seismic) loads needs the evaluation of higher order statistics even in the simplest case of normal distributed input.
Objective
In this paper, a non-linearization technique is proposed in order to evaluate the moments of any order of the response.
Method
This technique is developed by means of a nonlinear class of systems whose statistics are a priori known. The parameters of such systems can be chosen in such a way that the two systems are equivalent in a wide sense.
Result & Conclusion
In the paper, the strategy to obtain the equivalence and the reliability of the results are discussed.
1. INTRODUCTION
Seismic analysis and risk mitigation of existing constructions have been a main topic in the last decades. Many studies have been aimed to study different strategies to obtain a realistic prediction of the characteristics and the capacity of existing reinforced concrete as well as masonry structures [1-2]. As a consequence of a proper knowledge of the seismic capacity of structures, in the most cases, retrofitting or strengthening of them is required to improve the structural behavior according to the prescriptions of new regulatory codes. With this aim, a wide field of structural engineering is engaged in research of strategies comprising design methods for strengthening or energy dissipation systems of existing structural members [3-6].
Another important research field in structural dynamics is aimed to study structural hysteretic systems driven by stochastic input. The latter results of utmost importance because of not so much progress gained in the last years.
In structural dynamics, the term hysteresis is used to describe a non-conservative system behavior, in which the restoring force depends not only on the instantaneous deformation but also on the past history of deformations. For a cyclic motion, a plot of restoring force versus deformation forms a closed loop. The area of the loop is the energy loss of the system in one cycle.
The restoring force, since the system is of non-conservative type, cannot be obtained by a potential derivation. Two models of hysteretic behavior are usually referred to: the elastoplastic model, whose restoring force-deformation relationship is featured by an abrupt change of slope, and the smooth model proposed initially by Bouc [7] and extended by Wen [8-9] to give a more realistic description of the materials behavior.
As it is well known, in nonlinear stochastic systems, the statistic properties of the response are described by the probability function governed by the Fokker Plank Kolmogorov (FPK) equation.
Several studies were aimed to obtain exact or approximate analytical solutions of the FPK equation for nonlinear stochastic systems by using different methods and procedures such as the equivalent linearization method, equivalent nonlinear system method, complex fractional moments, stochastic averaging method, Monte Carlo simulation, path integration and generalized cell mapping technique [10-45].
In this paper, a non-linearization technique is proposed in order to evaluate the moments of any order of the response. This technique is developed by means of a nonlinear system whose statistics are a priori known. The parameters of such a system are chosen in such a way the two systems are equivalent in a wide sense.
2. MATHEMATICAL MODEL FOR HYSTERETIC SYSTEMS
Let the differential equation of motion of a single degree of freedom dynamical system be given in the form:
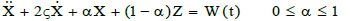 |
(1) |
where Z is the hysteretic component of the total restoring force and W(t) is the zero-mean normal white noise process whose Power Spectral Density (PSD) is constant at all frequencies (S(ω) = S0 , 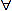 ω). The hysteretic restoring force Z can be often modeled by a first-order differential equation as follow:
ω). The hysteretic restoring force Z can be often modeled by a first-order differential equation as follow:
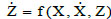 |
(2) |
The simplest case is the elasto-plastic model where Eq. (2) becomes:
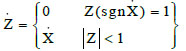 |
(3) |
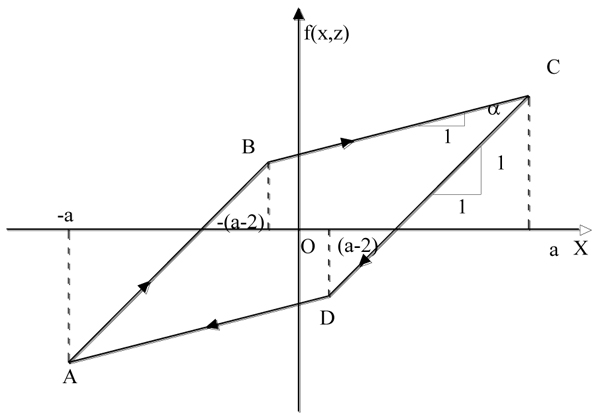
To give a brief description about the deformation of the system subjected to a variation of the restoring force, it can be assumed that the system is subjected to a certain level of force (Fig. 1). For the sake of simplicity, the initial stiffness is assumed unitary. Once a certain value of displacement is reached, the corresponding restoring force can be read along the straight line passing through the origin of the reference with a slope equal to the initial stiffness of the system.
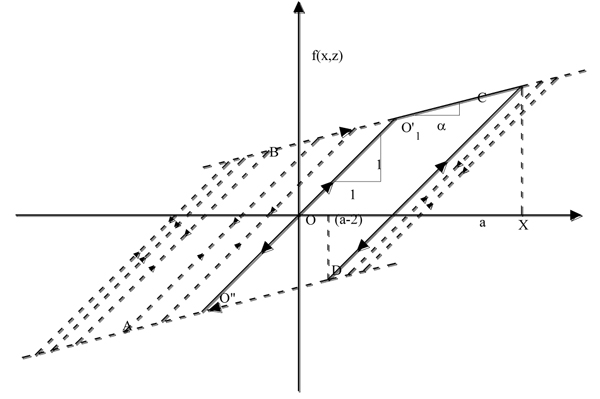
When the value of the deformation related to the point O' or O” reached with velocity  > 0 or
> 0 or  <0 respectively, the system follows the straight line BC (
<0 respectively, the system follows the straight line BC ( > 0) or the line DA (
> 0) or the line DA (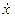 <0) until the accumulated energy level or the energy provided by the restoring force allow the system to keep positive or negative velocity respectively. At the same time, if the velocity keeps the same sign, the system cannot travel at different points with respect to the straight lines BC or DA, storing potential energy. As soon as all the energy of the system becomes potential energy, i.e. the velocity becomes null, the system tends to invert the sign of motion because it receives no other external energy.
<0) until the accumulated energy level or the energy provided by the restoring force allow the system to keep positive or negative velocity respectively. At the same time, if the velocity keeps the same sign, the system cannot travel at different points with respect to the straight lines BC or DA, storing potential energy. As soon as all the energy of the system becomes potential energy, i.e. the velocity becomes null, the system tends to invert the sign of motion because it receives no other external energy.
Assuming the system has reached the point C, it follows the straight line CD initially with negative velocity. Assuming that “a” is at the maximum deformation value reached on BC, the system remains on the straight line CD until one of the following situations occurs: i) crossing the CD line the maximum deformation reaches “a” with speed 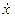 > 0 or ii) the maximum deformation reaches a-2 with velocity
> 0 or ii) the maximum deformation reaches a-2 with velocity 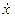 <0.
<0.
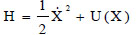 |
(4) |
It is worth noting that when the system is forced by a deterministic cyclic excitation then, in the steady state, the hysteretic force will describe a loop whose amplitude depends on the intensity of excitation (Fig. 2). At each cycle, the total energy H can be written as:
where U(X) is the potential energy, that is the work of the total restoring force from the generic position of the system to the non-forced position.
For the elastoplastic hysteretic system governed by Eq. (3), the potential energy U(X) has the analytical form:
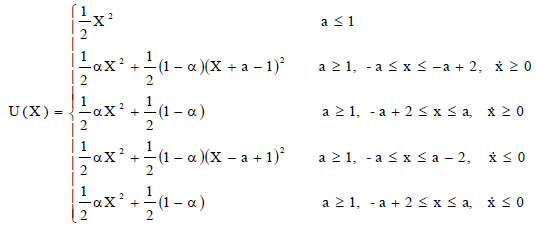 |
(5) |
obtained taking into account that the integration of Eq. (3) gives
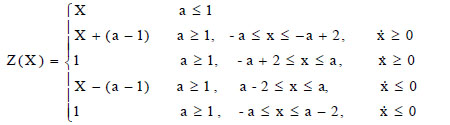 |
(6) |
Moreover, the extreme deformation a of the loop can be obtained as the positive root of the equation:
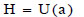 |
(7) |
being zero, at that point, the kinetic energy.
It is worth remarking that when the input is stochastic, the one to one correspondence between the values of the total energy H and the amplitude a(H) remains valid, taking in mind that all the system response variables are stochastic too.
Moreover, for a given value of total energy, that value is the maximum of the potential energy that the system can possess (corresponding to 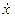 =0). Therefore, assuming a certain value of total energy, it is possible to define the maximum value of deformation a associated to the value of total energy by solving Eq. (7). This means that if an energy value H is assigned to the system, all the deformed configurations are included in the range [-a, a].
=0). Therefore, assuming a certain value of total energy, it is possible to define the maximum value of deformation a associated to the value of total energy by solving Eq. (7). This means that if an energy value H is assigned to the system, all the deformed configurations are included in the range [-a, a].
Another consideration to be made is that once the plastic deformation is reached by the system and it starts moving along the unloading straight-line, it does not retain any memory of the plastic deformation previously undergone.
3. RESTRICTED POTENTIAL SYSTEMS (RPS)
Let the differential equation of motion of a single degree of freedom dynamical system be given in the form:
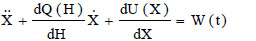 |
(8) |
where 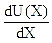 is a non-linear restoring force, dQ(H)/dH is the non-linear damping and W(t) is the zero-mean normal white noise process whose Power Spectral Density (PSD) is constant at all frequencies (S(ω) = S0 ,
is a non-linear restoring force, dQ(H)/dH is the non-linear damping and W(t) is the zero-mean normal white noise process whose Power Spectral Density (PSD) is constant at all frequencies (S(ω) = S0 , 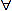 ω).
ω).
In Eq. (8), U(x) is a potential energy function and Q(H) is a non-linear function of the total energy H. The joint probability density function 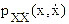 , obtained by solving the Fokker Plank Kolmogorov (FPK) equation associated with Eq. (8), for the stationary state, is given as:
, obtained by solving the Fokker Plank Kolmogorov (FPK) equation associated with Eq. (8), for the stationary state, is given as:
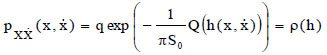 |
(9) |
h(x,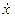 ) being the domain of
) being the domain of 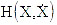 , that is:
, that is:
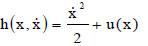 |
(10) |
while x, 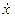 , u, as customary, are the domains X,
, u, as customary, are the domains X, 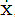 , U of respectively. In eq. 9, q is a normalization factor given by:
, U of respectively. In eq. 9, q is a normalization factor given by:
The function 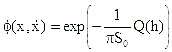 is defined as probability potential.
is defined as probability potential.
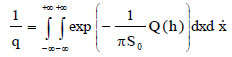 |
(11) |
The function dQ(H)/dH can be considered as a non-linear damping of the system. Here, it is assumed that Q(H) is a polynomial defined as follows
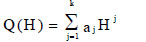 |
(12) |
where aj, j=1,2,......,k, are the coefficients of the polynomial. Eq. (8) describes a special class of potential systems which were called Restricted Potential Systems (RPS) in [28] to remember that it is part of a more extended class [19].
It is important to highlight that in Eq. (8) U(x) is a continuous function defined in the domain [-∞;∞] and only in these conditions the equation of FPK can be written and solved. In fact, if in Eq.(8) U(x) is defined as for Eq. (5), that is a discontinuous function, the system can no longer be considered as a potential system. However, if the function (5) is considered in the single portions in which dU/dX is defined as a continuous function, each of them can be associated with a potential system whose probability function is defined in [-∞;∞]. In particular, for each value of a, according to Eq. (5), four potential systems are obtained at most (a> 1). In these conditions, taking into account the form of U(X), Eq. (8) is representative of infinite potential systems that require infinite probability density functions of the state variables to be characterized. This does not constitute any limitation for the application of the equivalent non-linearization procedure already applied in the case of viscous dissipation systems in [28] for what will be said below.
In the case of a sinusoidal history of displacements with amplitude a, the behavior in terms of displacement and restoring force exhibited by the system represented by Eq. (8), in which the U (X) is expressed by Eq. (5), is shown in Fig. (3). The area enclosed by the cycle, also in this case, represents an energy dissipated by the system.
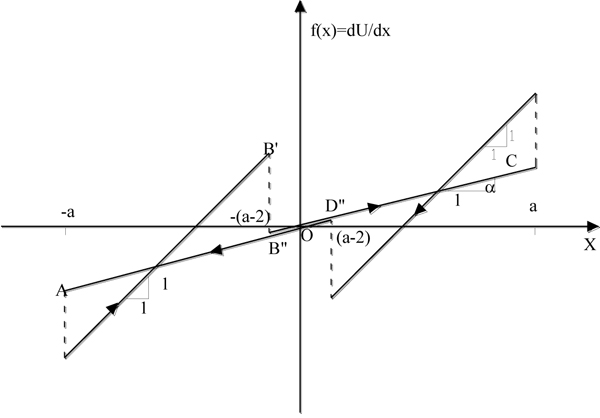
If one wants to describe how the restoring force varies depending on the displacement, suppose that the system is initially in the position O (Fig. (4) - unforced and undeformed) and from this position a force is applied. The system assumes first the positions defined by the 45° slope segment O'A. When the system reaches the position A with velocity  >0 or the position O' with velocity
>0 or the position O' with velocity  <0, the restoring force varies suddenly and the values on the straight line BD are assumed. Then, if the system reaches the position A' and the displacement increases, it assumes the restoring forces represented by the straight line BD until its velocity is greater than zero. If the velocity assumes the zero value in B (corresponding to a displacement equal to a) and the system invert its movement, then the restoring force varies suddenly again assuming the values represented by the straight line B'C with velocity initially negative but with the possibility to experiment positive values of the velocities until the displacement a is reached or the displacement a-2 is reached. In both cases, the system switches on the straight line BD (it is worthy to note that the straight line A'B and the straight line C'D are coincident but are drawn in such a way to be not perfectly superimposed in order to better understand the path of the system varying its displacement history). The system leaves the straight line DB when once again the velocity becomes null and the direction of the displacement is inverted.
<0, the restoring force varies suddenly and the values on the straight line BD are assumed. Then, if the system reaches the position A' and the displacement increases, it assumes the restoring forces represented by the straight line BD until its velocity is greater than zero. If the velocity assumes the zero value in B (corresponding to a displacement equal to a) and the system invert its movement, then the restoring force varies suddenly again assuming the values represented by the straight line B'C with velocity initially negative but with the possibility to experiment positive values of the velocities until the displacement a is reached or the displacement a-2 is reached. In both cases, the system switches on the straight line BD (it is worthy to note that the straight line A'B and the straight line C'D are coincident but are drawn in such a way to be not perfectly superimposed in order to better understand the path of the system varying its displacement history). The system leaves the straight line DB when once again the velocity becomes null and the direction of the displacement is inverted.
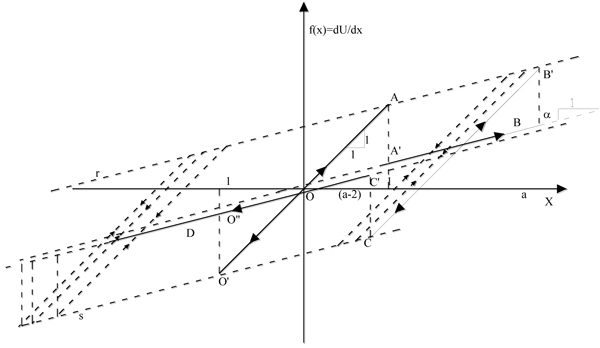
Therefore, the system can assume the configurations relative to all the straight-line segments parallel to O'A between the straight line r and the straight line s and configurations represented by the straight line BD. For each configuration, infinite velocity values and therefore infinite values of the total energy of the system can be observed. When the system moves on one of the infinite 45 ° straight lines, its motion does not depend on the accumulated plastic deformation.
From the comparisons between Figs. (2, 3) it is possible to see that the elasto-plastic system and the system obtained by a combination of an infinite number of RPS show a different behavior although both dissipate energy by hysteresis.
In the next section, the parameters of the model described by Eq. (8) will be obtained by means of an adequate procedure so that the equivalence with an elasto-plastic system will be obtained.
4. THE USE OF RPS IN THE EQUIVALENT STATISTICAL NON-LINEARIZATION OF HYSTERETIC SYSTEMS
Among the several methods able to determine the approximate solution of non-linear structural systems, one consists of replacing a given non-linear stochastic system by an equivalent non-linear one, whose exact steady-state solution is available. This technique, named equivalent statistical non linearization, was used by several authors [10, 14-15, 21-22].
Some of them have used potential systems for the equivalent non-linearization of hysteretic systems. In [14] the balancing of the energy dissipated by the hysteretic system and by the equivalent one is used as equivalence criterion. This method allows obtaining the form of the probability potential in terms of some double integrals. Unfortunately, it is not always possible to calculate closely these integrals so every value of the probability potential function depends on the numeric resolution of an infinity of double integrals.
If the equivalent non-linear system is chosen in the class of RPS, the equivalent non-linearization procedure can be easily applied, which will be shown later .
Referring to Eq. (1) and Eq. (8) as an equivalence criterion, the minimization of their mean square difference (E[ε2]) with respect to the coefficients aj of the polynomial Q(H) can be used, that is:
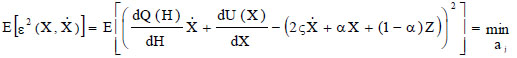 |
(13) |
Therefore, the coefficients aj can be obtained by the set of equations:
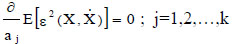 |
(14) |
By performing the derivatives in Eq. (14), the linear system:
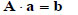 |
(15) |
is obtained. In Eq. (15) aT = [a1, a2 ..... ak], while the matrix A and the vector b are defined as follows:
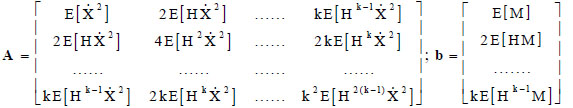 |
(16) |
where:
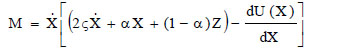 |
(17) |
The entries of the matrix A and the vector b are expressed as:
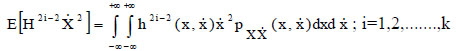 |
(18a) |
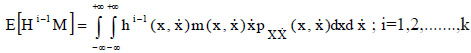 |
(18b) |
where 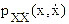 is given in Eq.(9). Since
is given in Eq.(9). Since 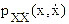 depends on the unknown coefficients aj, an iterative procedure has to be adopted to solve Eq.(15).
depends on the unknown coefficients aj, an iterative procedure has to be adopted to solve Eq.(15).
At this point, it is important to note that the averages contained in the left side of Eqs. (18 a-b) take into account all the possible configurations of the system (the ones defined by the infinite straight-line segments inclined at 45 degrees between the r and s lines (Fig. 4) and the straight line BD). It should not be forgotten that the infinite values of total energy can be associated with each of the deformed configurations, since the velocity values that the system can assume are infinite in a fixed point.
In order to obtain the values of the integrals (18-a) and (18-b), the following transformation of variables has to be done:
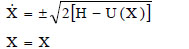 |
(19) |
The Jacobian of the transformation is:
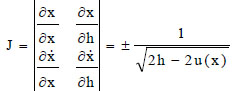 |
(20) |
The joint probability density of X and H is then:
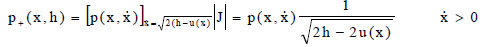 |
(21a) |
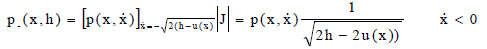 |
(21b) |
and the integrals (18-a) become:
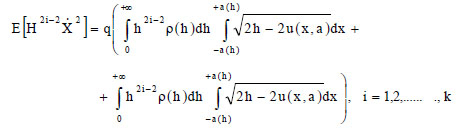 |
(22) |
where the function ρ(h) is defined in Eq.(9) and q being a normalization factor given by:
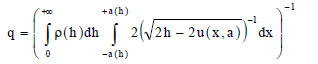 |
(23) |
while a is the maximum value achievable by the displacement for the assigned value of h and it is obtained by resolution of Eq. (7). In Eq. (22), the first term of the sum refers to all the states of the system having positive velocity, while the second one refers to all the states of the system having a negative velocity.
In this way, all the possible states of the system are explored and the variability U (x) can be taken into account depending on the state of deformation of the system and the load history.
If, on one hand, Eq. (22-23) present the advantage of being able to grasp all the possible states of the system at one time, on the other hand, the correct numerical calculation of the integral (23) can be difficult due to the presence of a singularity.
However an important fact can be observed: in the evaluation of the averages 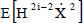 it is assumed that, with reference to Fig. (4), the set of straight line segments at 45° is explored and apart from these, the lines BD and O'A (for each of them a potential system is assigned); the averages calculated on each of the above segments do not depend on the value of the plastic deformation of the system; therefore, varying the plastic deformation the averages on these subdomains remain constant, moreover, if the system moves along the straight-line corresponding to the plasticization, the same averages assume always the same values. It derives that, in the evaluation of these averages, it can be considered that the system moves always along the unloading straight-line without plastic deformations.
it is assumed that, with reference to Fig. (4), the set of straight line segments at 45° is explored and apart from these, the lines BD and O'A (for each of them a potential system is assigned); the averages calculated on each of the above segments do not depend on the value of the plastic deformation of the system; therefore, varying the plastic deformation the averages on these subdomains remain constant, moreover, if the system moves along the straight-line corresponding to the plasticization, the same averages assume always the same values. It derives that, in the evaluation of these averages, it can be considered that the system moves always along the unloading straight-line without plastic deformations.
This is understandable by the fact that in its motion along the discharge lines the system does not preserve the memory of the plastic deformations experienced: plastic deformations do not change the possibility of accumulation of potential energy of the system nor its ability to acquire energy. If the plastic deformation does not influence the calculation of the averages in question, it is also true that the averages evaluated on the entire domain are equal to the average of the averages evaluated on all the possible domains of the system (the straight lines of type B’C), that are equal to each other.
This can be easily understood because the system does not store any memory of the plastic deformations during its motion along the unloading straight-lines. In other words, the plastic deformation does not change the possibility of accumulation of potential energy by the system as well as the possibility to acquire energy, therefore
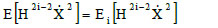 |
(24) |
where Ei is the average evaluated with respect to any domain in which the system is approximated by an RPS (lines of type B’C in Fig. (4)).
In conclusion, as it is obtained numerically, whatever the RPS potential system is approximating the hysteretic system, the averages of type 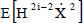 are always equal, and it is possible to study only one of all systems as for the case of the equivalent stochastic linearization based on RPS [28].
are always equal, and it is possible to study only one of all systems as for the case of the equivalent stochastic linearization based on RPS [28].
The above described results are of utmost importance because, if the moments contained in the matrix A can be calculated referring to a single potential system, then, it can be considered that between the moments contained in the matrix A, the following relationships can be assumed [28]:
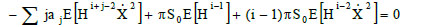 |
(25) |
(S0 is the constant level of the PSD of the input) and since it was demonstrated [28] that, for systems subjected to linear restoring forces, the following properties can be assumed:
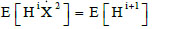 |
(26) |
this means that the matrix A is characterized by the moments of H and can be calculated once the probability density function of H is known according to [17] and once the first n-1 statistical moments contained in the matrix A are known. The others can be determined by means of Eq. (25) with considerable reduction of computational effort.
Regarding the averages of type E[Hi-1M] in Eq. (18-b), it can be observed that with the hypothesis of change of variables according to Eq. (19).
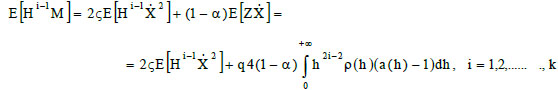 |
(27) |
with obvious meaning of the symbols. In Eq. (27) the calculation of the first term offers no difficulty thanks to Eq. (26).
5. NUMERICAL APPLICATION
In this section, a numerical application of the procedure above explained is presented by comparing the results with others criteria. The results provided by [17], in which a hysteretic bilinear system is subjected to a stochastic input with a variable amplitude of the PSD, are assumed as a reference. In detail, the PSD level (S0 ) was varied in the range of 0.0001-50 cm2/sec3. Moreover, the analyses were performed considering two systems, the first one is a pure hysteretic system and the second one is characterized also by a viscous dissipation with damping coefficient ζ=0.05.
In the first case, the equation of motion is
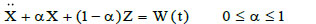 |
(28) |
while in the second case, the equation of motion is given by Eq.(1)
Varying the PSD level, input accelerograms were generated by means of the procedure in [46] and Eq.(1) and Eq.(28) were integrated for obtaining the system response histories in terms of displacement and velocity. Starting from these responses it was possible to evaluate the statistical of the response (or of the function of the response) by averaging and to perform the Monte Carlo simulation. Further at each PSD level, Eq.(15) was solved by an iterative procedure by the following steps:
- values of first attempt were assigned to the coefficients ai defining the equivalent RPS;
- Eq.(8) was solved and the averages appearing in Eq.(15) were calculated;
- Eq.(15) was solved to obtain a new set of coefficients ai defining the equivalent RPS;
- Coming back to step 2 to repeat the procedure;
The iterative procedure was stopped when the differences between coefficients ai calculated in two consecutive stages were lower than a fixed tolerance. Once the final set of coefficient ai was obtained, Eq.(8) was integrated for obtaining the response in terms of the history of displacement and velocity. These histories allowed to calculate the statistics of the functions of the response of interest for the present application.
It is worth noting that, for low values of the PSD of the input, the hysteretic behavior is struggling to activate itself compared to the behavior related to higher values of the PSD.
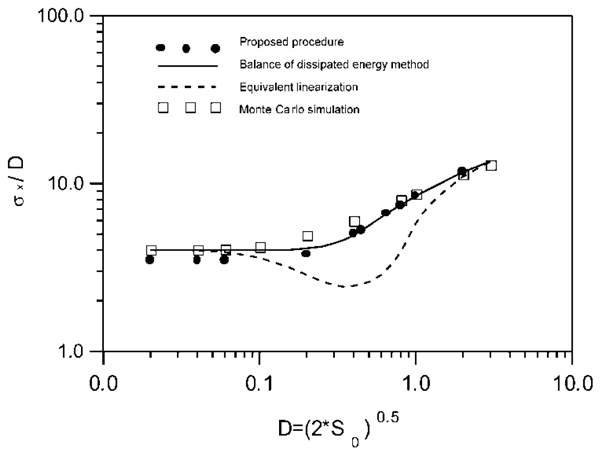
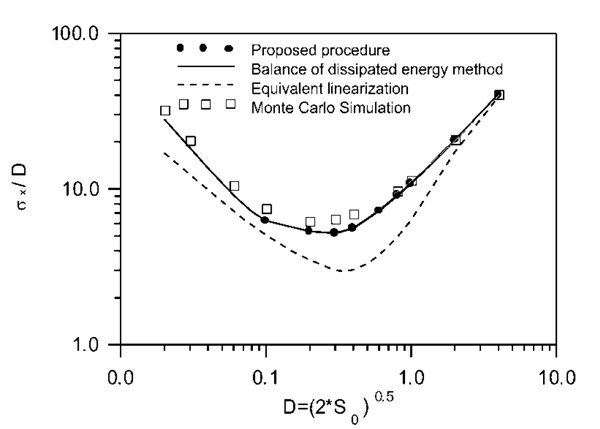
In Figs. (5-6) the standard deviation values of X (that is (E[X2]-E[X]2)0.5) normalized with respect to 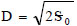 obtained by the pure hysteretic system and the system with viscous dissipation are shown. For all the excitation levels, the results obtained with the presented method agree well with the Monte Carlo simulation. Furthermore, the comparisons with the results obtained by [17] through the balance energy criterion show that the initial hypothesis about the analytical form of the equivalent potential system is not relevant for the accuracy of the results. From [17] it should also be noted that only information about the form of the probability density function can be found and a comparison in deterministic terms is not possible. Finally, at most three ak parameters are needed to identify the equivalent RPS.
obtained by the pure hysteretic system and the system with viscous dissipation are shown. For all the excitation levels, the results obtained with the presented method agree well with the Monte Carlo simulation. Furthermore, the comparisons with the results obtained by [17] through the balance energy criterion show that the initial hypothesis about the analytical form of the equivalent potential system is not relevant for the accuracy of the results. From [17] it should also be noted that only information about the form of the probability density function can be found and a comparison in deterministic terms is not possible. Finally, at most three ak parameters are needed to identify the equivalent RPS.
The proposed method fails in the case of the pure hysteretic system in correspondence with lower values of input due to the difficulty in the determination of the constant terms of the equivalent non-linearization algorithm. In this case, the term ζ is equal to 0 and therefore the constant term results 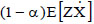 Eq. (27). Since the hysteretic behavior is not fully activated, these moments are close to zero, not ensuring the convergence of the algorithm. This does not invalidate the procedure for the poor engineering significance that takes the analysis for those values of the input.
Eq. (27). Since the hysteretic behavior is not fully activated, these moments are close to zero, not ensuring the convergence of the algorithm. This does not invalidate the procedure for the poor engineering significance that takes the analysis for those values of the input.
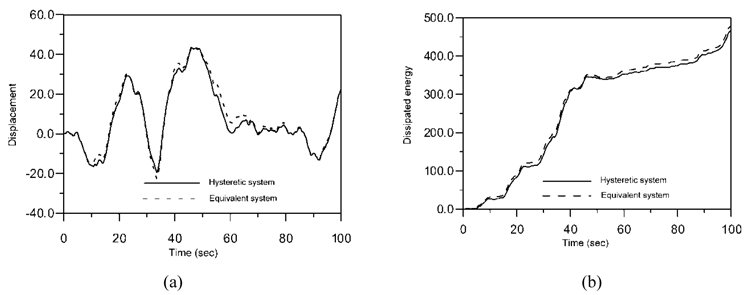
Comparisons of the displacement time histories of the elastic-plastic system characterized by α=1/21 e ζ=0.05 and of the equivalent system obtained by the proposed procedure are shown in Fig. (7a). While the energies dissipated by each system under the same input conditions are shown in Fig. (7b) (the input power spectral density S0 =2 cm2/sec3 was fixed). It is possible to denote that the deterministic analysis returns consistent results.
CONCLUSION
An equivalent non-linearization procedure for hysteretic systems was applied by using Restricted Potential Systems (RPS). The hysteretic systems considered are those with bilinear behavior. The procedure adopted, already available for systems with viscous behavior, was extended to the hysteretic system thanks to the statistical characteristics of the RPS.
The results of the proposed method were compared with that of the equivalent linearization and with the Monte Carlo simulation. It was demonstrated that by determining few parameters, it is possible to identify a system consisting of infinite potential systems and that the computational effort to obtain a good accuracy in terms of response statistics is low.
The results of the proposed method were compared with an available technique for the estimation of the statistics of the response of hysteretic systems, that is the energy dissipated balance method proposed in [17]. The reliability of the method was found to be in question and the very close results of the proposed procedure and the dissipated energy balance method. Nevertheless, the dissipated energy balance method is not able to give an equivalent simplified equation of motion for the evaluation of the time history of the response as possible by the proposed procedure. Further, by the dissipated energy balance method, it is not possible to obtain an analytical expression of the pdf for the calculation of the statistics of a generic function of the response.
The procedure here proposed, like the dissipated energy balance method, is at this moment presented in a form limited to simple systems whose response can be assumed as that of a single degree of freedom system.
LIST OF ABBREVIATIONS
| a | = displacement at the inversion of motion |
| a | = vector containing the coefficient defining the function Q |
| ai | = i-th coefficient defining the function Q |
| A | = matrix containing averages |
| b | = vector containing averages |
| E[.] | = average of the stochastic function in brackets |
| h | = value of the stochastic variable H |
| H | = stochastic variable (total energy) |
| J | = Jacobian |
| p(.) | = probability density function |
| Q(H), Q(h) | = function of the total energy defining the dissipation characteristics of a RPS |
| S0 | = value of the Power Spectral Density of a white noise |
| S(ω) | = value of the Power Spectral Density of the input for an assigned frequency ω |
| u | = value of the stochastic variable U |
| U | = stochastic variable (potential energy) |
| X | = stochastic state variable (displacement) |
| x | = value of the stochastic state variable X |
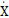 |
= stochastic state variable (velocity) |
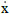 |
= value of the stochastic state variable |
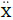 |
= stochastic state variable (acceleration) |
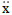 |
= value of the stochastic state variable |
| W | = Stochastic input (white noise) |
| Z | = hysteretic component of the total restoring force |
| α | = slope of the post elastic branch of the restoring force |
| ρ(h) | = function of the total energy corresponding to the pdf of a RPS |
| ω | = frequency |
| ζ | = damping coefficient |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


