All published articles of this journal are available on ScienceDirect.
A Simplified Approach for Analysis and Design of Reinforced Concrete Circular Silos and Bunkers
Abstract
Background:
Reinforced concrete silos and bunkers are commonly used structures for large storage of different materials. These structures are highly vulnerable when subjected to intense seismic forces. Available guidelines for analysis and design of these structures require special design skills and code procedures.
Objective:
The current study is aimed to elaborate the design procedures from different sources to a unified method, which can be applied to a larger class of reinforced concrete silos. In this study, analysis and design procedures are summarized and presented in a simplified form to make sure the efficient practical design applications of reinforced concrete silos.
Method:
Four different cases of silo design based on the type and weight of stored material were considered for the study. For each case, the silo was designed using given design procedure and modeled using FEM-based computer package. All of the reinforced concrete silos were subjected to gravity, wind and seismic forces.
Results:
After performing the analysis and design of different silos, the bending moment, shear force and axial forces profiles were given for a sample silo. The results obtained from the proposed design procedure were compared with FEM values for different components of silos such as slab, wall and hopper.
Conclusion:
The comparison of tangential and longitudinal forces, bending moments, shear forces and reinforcement ratios of different parts of silos have shown a fair agreement with the FEM model results. It motivates to use the proposed design procedure for an efficient design of reinforced concrete silos.
1. INTRODUCTION
Concrete comes in mind as the first option when we think about the construction of material storage facilities. Concrete has the ability to conform to any desired shape and also it's economical. Concrete proves to be a very useful material as it offers all the flexibilities in designing and construction of silos and bunkers which are required by any industry and foremost being in the economical limits.
Silo is an upright granular material storage tank. Such structures are constructed on higher elevations with an opening created at the bottom to collect the material. The term "silo" mainly incorporates two types of structures i.e. bin and bunker. Out of these two, the first one is the deep upright container while the second one is a similar structure with relatively shallow height. In case of bins if the plane of rupture strikes the opposite wall before emerging from the top of fill, that type is called deep bins while the other case is termed as shallow bins.
Importance of these storage structures has attracted the attention of many researchers worldwide to propose different load calculation methods and design considerations. ACI 1997 [1] is the only available guidelines, for the design of silo and bunkers. In addition to it, different researchers proposed different methods to compute the loads of moving and stacking material inside the silos and bunkers.
Silos can be made of steel or reinforced concrete.A typical group silo made of steel corrugated sheets is shown in Fig. (1). Silos are mostly cylindrical or rectangular in shape but can also be made of other shapes depending on the function and storage capacity of the material.

The design of silo is based on the density and angle of internal friction of material to be stored. Silo walls are subjected to lateral and vertical pressure caused by the materials. Accurate estimation of these forces and corresponding design of these structures is one of the recent challenges which many designers are facing. These storage structures become more vulnerable when subjected to the lateral earthquake forces. Failure of these structures is highly brittle and catastrophic.
Significant work has been completed in the field of designing the Silos. Most of the researchers have focused on only one of the components of Silo by using analytical and numerical methods. Dinghua and Jiping [3] researched on the lateral pressure acting on the walls of the reinforced concrete silo. The method of calculating the basic as well as the dynamic pressure acting on the wall of reinforced silo caused by the integral flow of granular material within the tower during discharge was also discussed. Zhen and Jin [4] analyzed and calculated the hoop stress in the reinforced concrete deep silo. The analysis results showed that the absolute value of hoop stress at the same height increases with an increase in height-diameter ratio but the absolute value decreases with an increase in the wall thickness. Kivanc and Baki [5] investigated the use of ferrocement in the construction of squat grain silos. It was concluded that ferrocement could be used in place of steel from the perspective of static as well as economy.
Because of high volumes and elevations, silos are highly vulnerable during earthquakes. If these structures are not properly designed, then earthquake can cause damage, and sometimes may result in complete collapse of silos. In 2001 during El Salvador earthquake, failure of silo had killed three people [6]. Out of vertical and lateral components of Earthquake forces, lateral components are more dominant and proportional to the height as well as weight of the material stored. On October 3, 1974 Lima, Peru Earthquake, a large grain silo situated in Callao got damaged at its head area. Fig. (2a) shows the partial collapse of this grain silo [7]. The possible cause of this failure was due to gravity loads and oscillation of material inside the silo. Fig. (2b) shows the failure of two reinforced concrete silos out of the group of three silos during the 1999 Kocaeli, Turkey Earthquake. According to Sezen et al. [8] the failure was not due to the stored material but due to deficient columns strength and deformation capacity.

Guo et al. [9] conducted a seismic vulnerability assessment of reinforced concrete silo considering granular material structure interaction. The seismic fragility assessment of the selected silo was performed using the incremental dynamic analysis. The analytical results showed that the hypo-plastic theory can be used to simulate the stored materials in the silo considering the collapse property before entering plastic state of the granular material. Neteghi and Yakhchalian [10] studied the seismic behavior of reinforced concrete silos considering granular material structure interaction. Modeling of earthquake effect on a reinforced concrete silo was done using finite element analysis. Many studies are there that describe the causes of the failures of silos. Theimer [11] discussed several instances of damaged grain silos and reasons for the failures and gave methods of assuming correct bin loads and designing reinforced concrete grain silos to prevent such failure. Dogangun et al. [12] provided a review and discussed common or spectacular silo failures due to explosions and bursting, asymmetrical loads created during filing and discharging, large and non-uniform soil pressure, corrosion of metal silos, deterioration of concrete silos die to silage acids, internal structure collapse, and thermal ratcheting. Silo damage and failures from several earthquakes were also presented in their study. Maj [13] presented some problems connected with the causes of reinforced concrete silos failure. It was pointed out that few reasons of appearance of horizontal and vertical cracks were temperature, pressure of stored material, live loads such as wind, dynamics character of wind, moisture, influence of construction joints, thermal insulation, chemistry active environment etc. that reduced the load carrying capacity of the walls of the silos and caused lower state of reliability. Dockrill et al. [14] performed a structural risk assessment of corroding infrastructure such as silos. The paper explored the difference between structural and corrosion risk and how each of these risk types should be considered in the assessment. Recently numerical studies have also been carried out to design and analyze silos. Durmus and Livaoglu [15] proposed a simplified 3 DOF elastic model for seismic analysis of silos. The distribution and the magnitudes of dynamic material pressures were estimated. Finally, the SDOF model was compared with FEM model. Wang et al. [16] developed a finite element model for pre-stressing reinforced concrete circular silo with large diameter using ANSYS. Average stress method was used to simulate the pre-stressed load on silo wall and inclined wall effectively. Fu et al. [17] analyzed the force condition of the silo wall. Strength analysis of reinforced concrete silo wall was based on finite element method. Sun et al. [18] researched on thermal stress of large diameter concrete silos. Inner force calculation formula of large diameter silo wall subjected to solid load and temperature action was derived based on cylindrical shell theory with the moment.
Work has been done in the field of dynamic design of silos and their behavior under earthquake. Silvestri et al. [19] described a series of laboratory tests that featured shaking table and a silo model, which were conducted in order to obtain some experimental data to verify the proposed theoretical formulations and to compare with the established code provisions. The results indicated that in all the cases, the effective mass is indeed lower than the Eurocode specification. The evaluation of the horizontal forces produced by grain like material inside silos during earthquakes was studied by Silvestri et al. [20]. Pieraccini et al. [21] refined the Silvestri theory for the evaluation of the seismic actions in flat bottom silos containing grain-like material. The refined theory confirmed that the portion of the ensiled material that interacts with the silo wall is significantly smaller than the effective mas suggested by Eurocode 8.
The literature survey clearly indicates that there have been numerous researches done on Silos but there is still lack of a formal step-by-step guideline to design a concrete silo. The current study is one of its own kind which not only discusses the analysis and design equations of different components of silos but also compares the Finite element analysis results with analytical and code values. Moreover different geometrical conditions of silo analysis and design are selected which correspond to the type of material to be stored in the silos.
1.1. Components of Silo
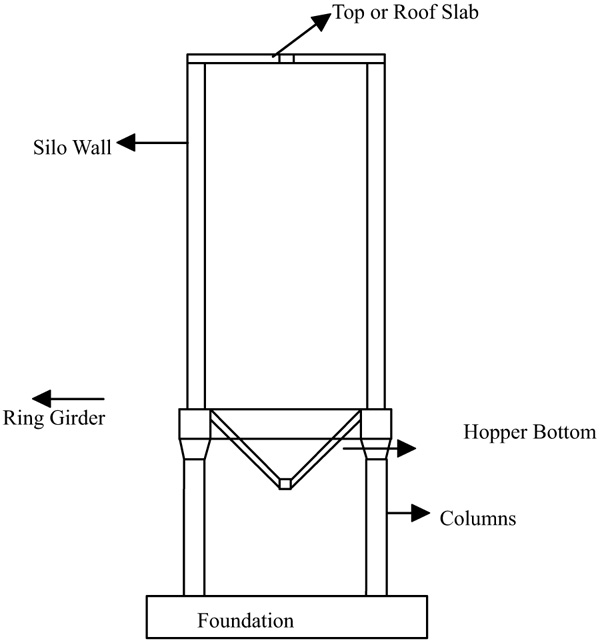
Fig. (3) shows a typical reinforced concrete or steel silo consisting of a silo wall, a hopper, roof slab, ring girder, supporting columns and foundations. Hopper is a funnel-shaped chamber or bin in which loose material is stored temporarily being filled from the top and dispensed through the bottom. The column is an upright pillar that supports the silo walls. Ring girder is a support beam that is used in silos whereas the foundation is the base of silo that connects it to the ground and transfers loads from the structure to the ground. The angle of hopper is decided based upon the type of material stored and the angle of internal friction of the material.
2. RESEARCH OBJECTIVES
In the current research study, a simple design procedure is presented based on the guidelines and recommendations proposed by different researchers for the safe and economical design of reinforced concrete silos. In order to get the required objectives, authors have gone through an extensive literature review and studied the methods proposed by different researchers and codes. Most of the available guidelines deal with only a particular issue i.e. in relation to the flow of material from silo, lateral forces due to the type of material, or estimation of earthquake forces at various components of silos. In the current study, all these guidelines are collected based on the recommendations of individuals and compiled into a single design procedure discussed in the later sections. In order to evaluate the adequacy of the given design procedure, four different cases of silo design were discussed in detail. These cases were decided based on the type and weight of materials to be stored in each silo. For each case, tangential and radial forces were calculated on silo walls and hopper. In order to verify the suitability of the proposed guideline, FEM-based numerical study was also carried out by using Sap 2000. The proposed guidelines have optimum values of forces on wall and hoppers and have provided a basis for the suitability of simplified proposed design approach for silos.
3. SILO DESIGN CONSIDERATIONS
Design considerations of silos are of two types: functional and structural. Functional design refers to the selection of proper hopper angle, operational safety, adequate storage of material, environmental and thermal protection of material stores and satisfactory methods for filling and taking the materials out of silos. Structural considerations are stability, strength and durability. A step by step approach using different formulae is given below in order to design a silo keeping in consideration all the factors affecting its performance. The formulae are taken from different sources and compiled in a way that the silo design becomes an easy and quick task.
3.1. Design Procedure of Circular Silo
Rectangular or square silos can also be used for storage of material but most commonly circular silos are used. The major fact behind this reason is economy. In rectangular silos, at the junction of two walls, there exists a bending moment, so there is a combined action of bending and tension, that results in more horizontal reinforcement as compared to circular silos.
In rectangular silos, wall pressure at longer and shorter sides also differs widely and results in a non-uniform pressure distribution in the hopper bottom, making the behavior more indeterminate. Circular silos provide more flexibility in the operation as compared to rectangular and square silos.If the slope of the hopper is not selected wisely, it may result in a dead storage on the hopper slope. For this purpose, it is strongly recommended to carefully model the material flow in the hopper bottom using a Finite Element Based computer package to avoid material stacking and flow problems. Circular hopper shapes were adopted in the study as they provide more operational convenience with less formation of dead zones.
The following section describes the design procedure for roof slab, silo wall, silo hopper with ring girder, hopper bottom and column design.
3.1.1. Slab Design Procedure
The main equations to calculate the moments werecomputed using Timoshenko and Woinowsky [22]. Radial and transverse moments were calculated as follows:
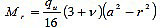 |
(1) |
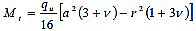 |
(2) |
Thickness of the slab was then computed by the equation given below:
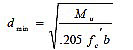 |
(3) |
d must be greater than the dmin whereas d = h - 27
Strength factor is calculated as:
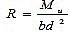 |
(4) |
In addition to the moments, it is also important to calculate the factored shear force for checking it against shear strength by using the following equation. This equation is taken from ACI 318 [23].
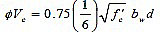 |
(5) |
3.1.2. Silo Wall Design Procedure
Deciding whether the bin is silo or a bunker is the first step towards designing the silo wall. The following procedure is used for the design [24].
-
if
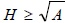 the bin is a silo else bunker
the bin is a silo else bunker
- if H ≥ 1.5 D for circular silo, the bin is a circular silo else bunker
- if H ≥ 1.5 a for rectangular silo, the bin is a rectangular silo else bunker
Wall thickness of the silo is computed using the following formula that is given in Portland cement association PCA [25].
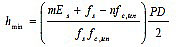 |
(6) |
Ring Girder Design
One important thing in the design of ring girder is that the centroid of the ring girder should coincide with the centerline of the wall and the supporting column.
Using the coefficient given by Mark and Fintel [26], the maximum positive and negative moments were calculated as follows:
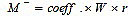 |
(7) |
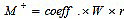 |
(8) |
3.1.4. Hopper Bottom Design
After calculating the weight of the material in hopper and the weight of hopper itself, Fmu and Ftu are calculated using the following formulae [26]:)
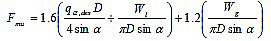 |
(9) |
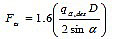 |
(10) |
3.1.5. Column Design
During the column design procedure, the loads acting on the column are calculated. It is also determined if the column is short or long.
The suitable diameter of the column is selected by employing the following equation [27]:
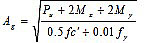 |
(11) |
The required amount of reinforcement is computed using the following formula [27].
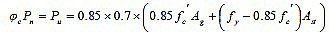 |
(12) |
4. MATERIAL PROPERTIES AND MODELLING PARAMETERS
Tables 1a and 1b show the material properties, geometrical properties and loading on the silos, respectively. The compressive strength of the concrete slab was selected as 17.25 MPa and for all other silo components, the compressive strength was fixed to 25 MPa. A 200 mm thick slab was provided with a 1.5 m opening at its center for material inflow. The wall thickness of silo was taken as 250 mm and that was decided based on equation 6. The size of each silo was based on the weight of material stored. Table 1b provides the geometrical properties for Case-1 (Coal). For all other cases, the material properties remain the same, however, the geometrical properties were different based on the type and weight of the material stored. Table 2 provides the loading parameters on silos. All parameters in Table 2 were the same for all silos except the stored material unit weight and its angle of internal friction with concrete. The earthquake loading on the silos was calculated as per UBC-97 [28]. A seismic zone of 2B with a soil profile of class C is considered. The silo was subjected to a wind speed of 140 KMPH which is the maximum expected wind speed in the urban areas of Eastern province of Saudi Arabia.
| Parameter | Value |
|---|---|
| Compressive Strength of Concrete Slab | 17.25 MPa |
| Yield Strength for Slab Steel | 300 MPa |
| Slab thickness | 200 mm |
| Concrete Compressive Strength of Wall, Hopper, ring girder and columns | 25 MPa |
| Yield Strength for Steel | 420 MPa |
| Silo Wall Thickness | 250 mm |
| Width of Ring Girder | 600 mm |
| Depth of Ring Girder | 1125 mm |
| Unbraced length of column | 8.0 m |
| Unit Weight, | γ = 77 kN/m3 |
| Ultimate Strength, | Fu = 400 MPa |
| Modulus of Elasticity, | E= 200 GPa |
| Load | Value |
|---|---|
| Collateral Load on Silo Slab | 0.5 N/m2 |
| Angle of internal friction | 27 o |
| Stored Material Unit Weight | 8.64 N/m3 |
| Live Load on Slab | 1.50 kN/m2 |
| Designed Wind speed | 140 Km/hr |
| Windward wind pressure | 0.875 kN/m2 |
| Leeward wind pressure | -0.875 kN/m2 |
| Wind Exposure Category | C |
| Open Conditions | Fully Enclosed |
| Seismic Zone | 2B |
| R | 3.5 |
| Soil Profile Conditions | Soil Type -C |
| Sr. No. | LRFD |
|---|---|
| 1 | 1.4DL |
| 2 | 1.2DL+1.6LL |
| 3 | 1.2DL+1.6LL+0.8WL |
| 4 | 1.2DL+1.0EQ |
| 5 | 0.9DL+1.6WL |
| 6 | 0.9DL+1.0EQ |
The silos were modeled by using SAP 2000. Shell rectangular element type was selected for analysis. Each silo wall and hopper was divided into 600 rectangular shell elements. The elements located at the top of the walls were having the unrestrained condition at the topmost nodes whereas all other internal elements were restrained. Ring girder and column were considered as line elements. The elements at the base were assigned fixed end boundary conditions. Material non-linearity was considered by giving the non-linearity parameters in Sap 2000. A similar kind of nonlinear concrete modeling was adopted by Mokhatar et al. [29] and Sabah et al. [30, 31] to evaluate the impact responses of concrete slab and bio-inspired sandwich composite beams, respectively.
4.1. Wind Loads
The wind loads acting on the mainframes are determined in accordance with ASCE/SEI 7-10 [32]. Wind loads are governed by wind speed, exposure category and open wall conditions of the silos. Wind design pressure p depends on Importance Factor Iw, velocity pressure q and pressure coefficient GCp as calculated by using equation 13 [32]:
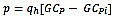 |
(13) |
Where velocity pressure q is evaluated by using the following equation:
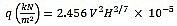 |
(14) |
4.2. Earthquake Load Calculation
UBC-97 [28] is commonly specialized in seismic load calculations. According to the location of the seismic zone of the building with some categories, this code provides a number of different coefficients to perform these calculations. According to UBC-97, the total design base shear can be determined by using equations 15 to 18:
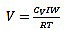 |
(15) |
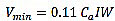 |
(16) |
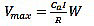 |
(17) |
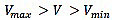 |
(18) |
The total force is distributed over the height of the structure in conformance with UBC-97 formulas given as follows:
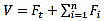 |
(19) |
The concentrated force Ft at the top, which is in addition to Fn, is determined by Eq. (20):
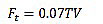 |
(20) |
The value of T is the period as 0.7 second or less. The remaining portion of the base shear is distributed over the height of the structure, including level n, according to Eq. (21):
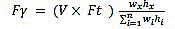 |
(21) |
4.3. Load Combinations
The design of silos was conducted by adopting the design load combination given by Table 2. The load combinations were taken from the ASCE/SEI 7-10 Minimum design loads for building and structures [32].
4.4. Element Type and Mesh Density.
The concrete is discretized with a 3D, 8-node hexahedron solid elements keeping a minimum element size of 500 mm depending on the height and diameters of silos. Bi-Linear behavior of steel is considered and steel elements are embedded in the concrete material.
4.5. Concrete Behavior Modeling
Concrete behavior was modeled using the concrete damage plasticity model available in SAP 2000. This model considers the compression crushing and tensile cracking as two major failure mechanisms. In addition, the concrete damage plasticity model requires the five damage parameter along with the modulus of elasticity and poison's ratio. The value of the poison's ratio is chosen as 0.2. For the uniaxial compression behavior of concrete, a linear stress-strain relationship is considered up to the 50% of peak strength (fc'). The remaining compression curve is derived using the expression proposed by Carreira, and Chu [33] as given in Eq. (22) and (23).
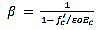 |
(22) |
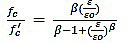 |
(23) |
Where, ε0 and Ec values were calculated as proposed by Ahmed [34] and ACI-318 [35], respectively,
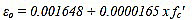 |
(24) |
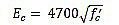 |
(25) |
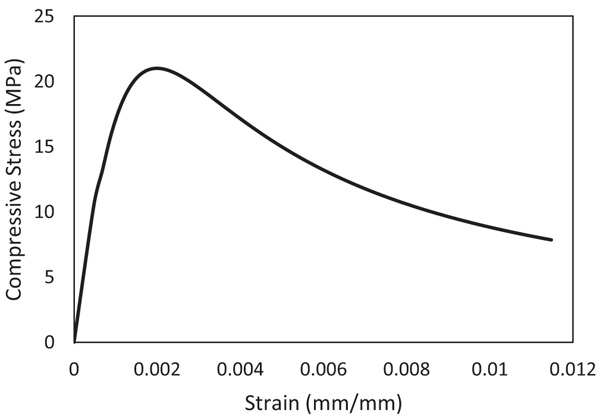
The complete stress-strain curve of concrete under uniaxial compression is presented in Fig. (4).
Concrete tensile behavior is assumed as linear elastic until the initiation of cracking corresponding to tensile strength (ft') that is calculated by Eq. (26).
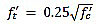 |
(26) |
5. DIFFERENT CASES OF SILO DESIGN
In order to validate the design results, four different cases of loadings were considered. The weight and type of stored material were the main criteria for these cases under consideration. The following Table (1b) gives the details of the cases ranging from 1 to 4. The materials selected for four cases were coal, wheat, cements and oats. Each material has its own unit weight and angle of internal friction as shown in Table 3. The size (diameter and height) was decided based on the weight of stored material and ratio of wall height/diameter ratio. For better operation of silos, Height/Diameter ratio should be between 1.5 to 2.0 [1]. The manual design was conducted for each case and the results were compared in terms of forces and stresses.
| Case No. | Material | Design Capacity (Ton) |
Unit Weight (kg/m3) |
Angle of Friction | Silo Diameter (m) |
Wall Height (m) |
Total Height (m) |
|---|---|---|---|---|---|---|---|
| Case 1 | Coal | 2050 | 8.64 | 27 | 12 | 23 | 26.2 |
| Case 2 | wheat | 320 | 7.84 | 23 | 7 | 12 | 13.7 |
| Case 3 | Cement | 1375 | 15.7 | 30 | 9 | 15 | 17.3 |
| Case 4 | Oats | 1960 | 6.21 | 20 | 12 | 28 | 31.8 |
5.1. Application of the Procedure
A single circular reinforced concrete silo for storing coal is designed with the help of the procedure mentioned above. Dimensions of the silo chosen were based upon the weight of stored coal which is 2050 Tons. The walls of the silo were resting on ring girder, which in turn was supported by eight columns. The foundation consists of a circular beam and a spread footing slab. Firstly, the components of silo were designed and then the detailing of each component was carried out.
The results are shown and compared in the following sub-sections i.e. Tables 1b and 2.
5.2. Computer Aided Analysis
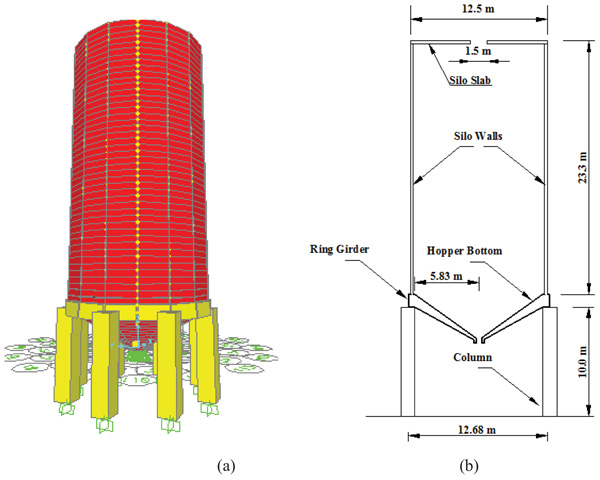
Finite element analysis is done using SAP 2000 software. The geometrical model with dimensions of the silo modeled is shown in Fig. (5a, b).
5.3. Force Distribution Contours
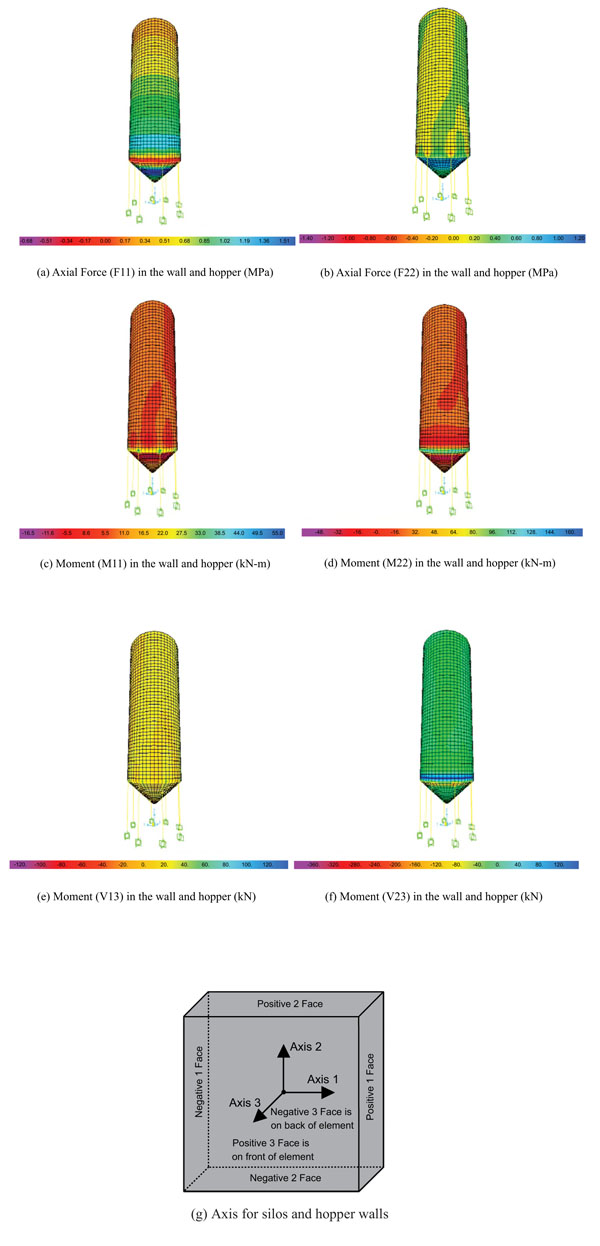
Fig. (6) shows the axial stress, bending moment and shear force diagrams for the silo designed and analyzed for case-1 with respect to axis 1, 2 and 3. Axis 1 and 2 are along the wall and hopper while the axis 3 is perpendicular to both. The positive force F11 corresponds to the axial force along the axis 1 on face 1: similarly shear V13 means the shear force along axis 1 of face 3. Fig. (6a) shows the axial stress concentration along the axis 11. F11 corresponds to tangential stress in the wall and hopper. Positive values mean tensile tangential stress and the negative value shows compressive tangential stress. It could also be seen in Fig. (6a) that the tangential stresses are minimum at the top and increase as we go deeper into the silos. Maximum tangential stresses are spotted near the bottom of the hopper. The value of peak tangential stress is around 1.53 MPa, which is within the allowable tensile stress of the concrete. The presence of hoop beam at the junction of hopper and wall caused negative or compressive stresses closed to the junction as shown in Fig. (6a). The axial stress distribution of silo wall and hopper for the only material live load is shown in Fig. (6b). The longitudinal stresses remain tensile throughout the height of the wall within the range of 0.2 MPa to 0.4 MPa. The concentrated compressive zone was spotted above the columns with the stress values closer to 0.8 MPa. The maximum tensile stress was found near the junction of wall and hopper wall has shown tensile behavior and stresses remained within the limit of 1.0 MPa to 0.8 MPa. The longitudinal stress mainly depends on the material flow pattern and the zone of zero longitudinal stress was spotted in the silos walls. Figs. (6c and d) show the bending moment about 1 and 2 axis, respectively. The minor axis moment in silo walls remained less than 5.5 kN-m whereas the major moment M22 was found around 16 kN-m. A higher concentration of moments was observed at the bottom of silos walls. Due to the slope surface, these values were significantly higher for hopper as the maximum values of 16.5kN-m and 48.0 kN-m were spotted for M11 and M22, respectively. Fig. (6e and f) show the shear forced distribution in silo walls and the hopper for live loads only. Due to the increase in tangential forces and depth of storage, the shear V23 was significantly higher than shear V13. The shear V13 did not show a wide distribution of shear force values as the shear forces in the wall remained in the range of -20 - 20 kN. However, in case of shear V23, a very high concentration (120 kN) of shear forces was found at the junction of hopper and silo wall. Fig. (6g) shows the axis for silos and hopper walls.
6. DISCUSSION
It can be seen from the Tables 4-6 that qualitatively, there is an agreement between the analytical and numerical values. However, there is some difference in the values quantitatively. At the very top of the silo wall, the percentage error in the analytical and numerical value of tangential force is about 38% for all of the four cases. This error decreases to about 2% as one move downwards to the center of the silo. The decrease in the error can be contributed to the fact that there is more pressure on the silo wall due to material and the material is in stationary condition at this point. Near the junction of the silo wall and the hopper, the error again increases due to the complicated dynamics of the movement of the material that is passing from the main silo to the hopper. In the hopper, again the same trend is observed. The area near the junction has a percentage error in the value of about 36% which decreases to 15% when the values are calculated away from the junction and closer to the end of the hopper. For longitudinal force in the hopper, the percentage error is the least at hopper junction and it increases as one moves closer to the end of the hopper. The top end of the beam shows about 20% percentage error in the values of moment and reinforcement and for the bottom end, this error increases up to about 35%. For the shear force in the beam, the error is again about 20%. The analytical and numerical values of the reinforcement are very close to each other. It can be concluded that for the silo wall tangential force, moments and shear in the beam, the analytical calculated values are higher than the numerical values whereas this trend is reversed in case of hopper longitudinal force and the beam reinforcement calculations.
| Case no. |
Depth (m) |
F(Tangential Force, Analytical) |
F(Tangential Force, Numerical) |
% Difference |
F(Longitudinal Force, Analytical) |
F(Longitudinal Force, Numerical) |
% Difference |
|---|---|---|---|---|---|---|---|
| Case-1 | 6.114 | 213.12 | 131 | 38 | |||
| 10.33 | 341.76 | 337 | 1.2 | ||||
| 23 | 619.7 | 534 | 13 | ||||
| 24.125 | 878.75 | 1183.25 | 25 | 727 | 1193 | 39 | |
| 25.17 | 304.8 | 411.12 | 26 | 497 | 527 | 5.6 | |
| 26.17 | 17.73 | 20.52 | 15 | 57 | 170 | 66 | |
| Case-1 | 2.92 | 66.2 | 40.7 | 39 | |||
| 7.46 | 156.1 | 153.9 | 2 | ||||
| 12 | 811 | 698.8 | 13 | ||||
| 12.9 | 188 | 155.84 | 17 | 259.9 | 262.04 | 0.7 | |
| 13.3 | 70 | 114.14 | 38 | 94.35 | 120.94 | 22 | |
| 13.7 | 6.98 | 22.4 | 68 | 8 | 66.3 | 87 | |
| Case-3 | 4 | 217.94 | 134 | 61 | |||
| 9.5 | 481.90 | 475.2 | 1.2 | ||||
| 15 | 668.52 | 576.1 | 13 | ||||
| 15.775 | 501.88 | 415.25 | 17 | 562.18 | 566.75 | 0.7 | |
| 16.525 | 136.1 | 222 | 38 | 159.1 | 264.5 | 39 | |
| 17.275 | 10.4 | 33.45 | 69 | 11.45 | 94.85 | 88 | |
| Case-4 | 6.995 | 170 | 104.5 | 38 | |||
| 17.5 | 385 | 380 | 1.2 | ||||
| 28 | 529.1 | 456 | 13 | ||||
| 29.2 | 815.75 | 675 | 17 | 864.36 | 871.5 | 0.8 | |
| 30.75 | 202.2 | 330 | 38 | 318.2 | 408 | 22 | |
| 31.75 | 13.8 | 44.4 | 68 | 14.9 | 123.4 | 88 |
| Case no. | Location |
Moment (Manual) (KN-m) |
Moment (Computer) (KN-m) |
% Difference |
As (Manual) (mm2) |
As (Computer) (mm2) |
% Difference |
|---|---|---|---|---|---|---|---|
| Case1 | Top | 1384.3 | 1089 | 21 | 3704.4 | 3917 | 6 |
| Bottom | 696.32 | 439 | 36 | 2100 | 2168 | 3 | |
| Case 2 | Top | 167.54 | 131.8 | 21 | 766 | 810 | 6 |
| Bottom | 86.44 | 54.5 | 37 | 393 | 404.7 | 3 | |
| Case 3 | Top | 1180.2 | 928.44 | 21 | 4123 | 4360 | 6 |
| Bottom | 595.05 | 375.15 | 36 | 2000 | 2065 | 3 | |
| Case 4 | Top | 1976.72 | 1555 | 21 | 4968 | 5253 | 6 |
| Bottom | 994.33 | 627 | 36 | 2410 | 2488 | 3 |
| Case no. |
Shear (Manual) (KN) |
Shear (Computer) (KN) |
% Difference |
|---|---|---|---|
| Case1 | 1744 | 1395 | 20 |
| Case 2 | 345.53 | 276.4 | 20 |
| Case 3 | 1106.02 | 855 | 22 |
| Case 4 | 977 | 782 | 19 |
Comparison of the analytical and numerical results shows that manual calculations are in general very close to computer results. However, some results do not follow a fixed pattern. Computer results were somewhat mysterious as the comparison of hoop stresses in the wall showed that values given by computer were smaller than the values obtained from manual calculation but when the results in the conical hopper were compared, the same tangential stresses computed manually (Ftu) were smaller than the values obtained from the computer. For each case, different percentage difference was spotted as the hoop and tangential stresses are not proportional and are the function of silo diameter and wall thickness. In majority of the cases, the values given by the code or analytical procedure were higher. However, in case of hopper, the trend was opposite and which motivated to further explore the analytical hopper stresses. Similarly, although the results of beam moments are very close to moments calculated analytically with the computer results, for moments lesser than the manual results, on the other hand, more reinforcement is given by computer program for same moments as conformed to manual results.
CONCLUSION
A detailed analytical and numerical study on the different type of silos was conducted to evaluate the existing load calculation procedures and design methodologies. Silo height, diameter and unit weight of stored materials were the parameters of the study. Following are some of the key findings of the study:
- A careful selection of silo geometry plays an important role as deeper silos results in higher values of lateral forces acquiring thicker silo walls and deep foundation for the column or walls.
- The analytical procedure for the calculation of load has given the analysis results very close to that of their FEM modelling values given by the computer. In general, the computer results for the analysis and design are very close to the analytical values. However, minor difference in moments and tangential forces was found among computer and analytical values.
- In case of tangential and longitudinal forces in silos walls, a good comparison of numerical and analytical forces have been established. However, this percentage difference increases in case of hopper. It motivates to further explore the force calculation procedure of hoppers.
- The method proposed for the calculation of forces in the silo wall is more conservative than the computed values. But, for silo hopper bottom, it has been found that the values or forces predicted by the computer were more than the analytical values. It is suggested to further explore the existing methods for force calculations in the hopper.
- In the case of line components of silos such as columns and ring beams, good agreement between the analytical and numerical design forces has been achieved.
- For most of the cases, the reinforcement design values of analytical and computer were also in fair agreement. But, in some cases, the values given by the computer were slightly higher due to some detailing and secondary design requirements.
LIST OF ABBREVIATIONS
| Mr | = Radial moment |
| Mt | = Transverse moment |
| qu | = Factored slab load |
| a | = Radius of slab |
| r | = Point of moment calculation |
| Mu | = Factored moment |
| fc' | = 28 days concrete compressive strength |
| b | = Width of slab design strip |
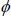 |
= Strength reduction factor |
| m | = Coefficient of concrete shrinkage |
| Es | = Modulus of elasticity of steel |
| Ec | = Modulus of elasticity of concrete |
| fs | = Allowable stress in steel |
| M+ | = Positive moment |
| M- | = Negative moment |
| W | = Weight acting on hopper |
| Fmu | = Factored longitudinal force |
| Ftu | = Factored tangential force |
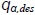 |
= Design static pressure in silo hopper |
| Ag | = Gross cross-section area |
| Pu | = Factored axial force in column |
| fc, ten | = Allowable tensile concrete strength |
| P | = Transverse force in the wall |
| D | = Diameter of silo |
| Mx | = Factored moment in x-direction of column |
| My | = Factored moment in y-direction of column |
| fy | = Yield strength of steel |
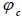 |
= Strength reduction factor in column |
| n | = Es / Ec |
| Fm | = Meridional forces in hopper |
| Wl | = Weight of the material |
| Wg | = Self-weight of hopper and the material |
| alpha | = Angle of the hopper wall with the horizontal |
| DL | = Dead Load |
| LL | = Live Load |
| WL | = Wind Load |
| EQ | = Earthquake Load |
| p | = Design wind pressure in kN/m2 |
| qh | = Velocity pressure in pounds kN/m2 |
| GCp | = External pressure coefficient |
| GCpi | = Internal pressure coefficient |
| q | = Velocity pressure |
| V | = Total design base shear |
| W | = Seismic dead load, used to calculate the base shear. |
| Vmax | = Maximum allowable design base shear |
| Vmin | = Minimum allowable design base shear |
| Cv | = Coefficient dependent on the soil condition at the site and seismicity of the region |
| Ca | = Another seismic coefficient dependent on soil conditions and seismicity of region |
| I | = Seismic importance factor, used to increase margin of safety |
| R | = Structural system coefficient, measures the ductility and over-strength of the system |
| T | = Fundamental period of the structure in the direction under consideration |
| Ct | = 0.035 for steel frames |
| hn | = Height of the building in feet |
| Fi | = The force at each level according to the height of the structure |
| Ft | = Extra Force in addition to Fi |
| wx | = The weight at a particular level above the base shear |
| hx | = The height at a particular level above the base shear |
| Wi | = The Total Weight |
| hi | = The total height |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


