All published articles of this journal are available on ScienceDirect.
A Numerical Model for Pre-Monitoring Design of Historical Colonnade Courtyards: The Case Study of Chiaramonte Palace in Palermo
Abstract
This paper proposes a numerical model that can be used for theoretical and experimental dynamic characterization of historical colonnade courtyards. Such an architectural element appears often in buildings of historical heritage and, especially under seismic excitation, it represents the most vulnerable structural part. Therefore, it is very important to have reliable as well as simple models available for vulnerability analysis, to evaluate different reinforcing systems if needed, or to plan dynamic characterization tests or monitoring campaigns, as in the present case. Chiaramonte Palace, a wonderful example of the historical heritage of Palermo, is investigated as case study. Firstly, a review of the restoration and structural consolidation works made over the years is presented, as fundamental step towards the knowledge of any existing structural system. Then the acquired information are used to propose a simplified finite element model that properly accounts for the interaction with the surrounding part of the building, and that can be easily calibrated on the basis of estimated or measured vibration periods.
1. INTRODUCTION
Cultural heritage preservation monitoring is based on three main steps: i) material analysis, ii) mathematical modeling, iii) dynamic tests. Each phase is not independent of the other, in fact modeling needs of the test results which in turn need the modeling for the best choice of sensors positioning. From here it follows that it is necessary as a preliminary step of monitoring, a simplified numerical model where the materials will be characterized through the results of the tests on the materials themselves. Moreover, such a numerical model should be based on a simple structural schematization to highlight the dynamic characteristics such as fundamental frequencies and mode shapes. From the scheme will be an indication of the best location of the sensors. Then results of the testing data will also be used to refine the mathematical model that will predict the structural behavior to various external events. This paper proposes a mathematical model as a basis for monitoring simple and useful for analyzing the dynamic behavior of historical colonnade courtyards a constructive element recurring in the historic buildings, (museums, churches, etc.) staring from a case study: Chiaramonte Palace. Chiaramonte Palace, known as ‘Steri’, is a rare and precious example of fourteenth-century architecture in Sicily. It is located in the “Marina” (Fig. 1), hinge between the harbor and the city of Palermo, and part of the ancient quarter of Kalsa. The building dates back to 1320 and it was built, according to Giuseppe Spatrisano [1], by Giovanni Chiaramonte ‘the Old’, admiral of the kingdom of Aragon. The role of the customer justifies its dimensions and typological peculiarities: its squared floorplan, gravitating on a porticoed courtyard, provides broad delegation rooms for public assemblies. The “hosterium” still manifests the power of a fortified palace, despite it was altered several times and used for different scopes since the fifteenth century. Numerous changes and restorations, more or less invasive, occurred over the centuries, from 1726 to 1973 up to the last extensive restoration ended in 1998. In particular, the restoration carried out in 1973 by Roberto Calandra and Carlo Scarpa, when the building becomes the Rectorate of the University of Palermo, leaded to extensive modifications that converted part of the historic building, the “Osterio”, into offices, exhibition areas and museums [2]. The square plan of the palace, with a side of about 40 meters, consists of four wings surrounding the magnificent courtyard, with its portico on the ground floor and the upper loggia, that anticipates the mansion Renaissance model, accessible from a vestibule on the east side of the building (Fig. 2).
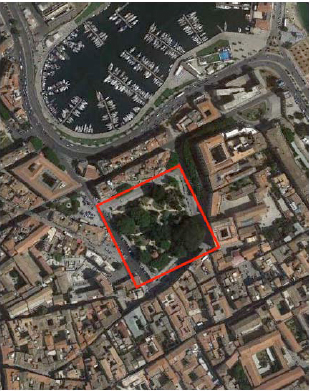
The plain of "Marina".

Satellite view of Chiaramonte Palace in Palermo with its four wings (dots).
2. THE COURTYARD
2.1. The Structure of the Courtyard
The magnificent dual arcade courtyard (Fig. 4a), sur-mounted by a terrace, presents essential shapes with ogival arches resting on columns. It extends over an area of about 420 m2, with a 20.25x20.40m squared plan and an overall height of 19.50m, on two levels. Main geometrical dimensions are reported in Fig. (4b), Fig. (5b), Fig. (6b), Fig. (7b). The portico (Fig. 5a), as almost the entire bulding, is made of calcarenite stone: the columns, the arches, as well as the above masonry, are composed by medium-large compact blocks.
The courtyard (Fig. 3) is the dominant architectural element of the building and it is the object of the present study.

Courtyard: top view of the portico and loggia.
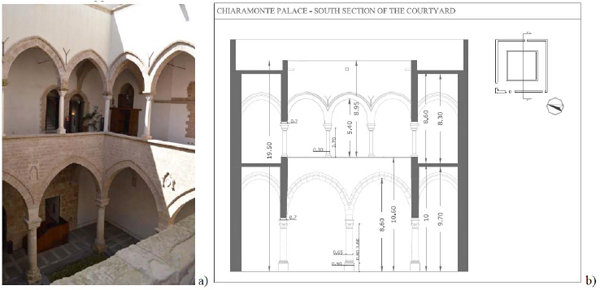
The courtyard: (a) dual arcade courtyard; (b) south section of the courtyard.
The masonry of loggia (Fig. 6a), instead, is made of irregular stones and, during last restoration [3], was improved by glass fiber reinforced mortar injections. Its columns, smaller than those of ground floor, are made of marble, with different shapes.
At second floor, on the terrace (Fig. 7a), there is the famous "hall of capriate", whose adaptation to an art gallery was long debated in the early years of the twentieth century. This part of the building never suffered changes in the years, except for the slab [4]. In fact, all the floor slabs of the courtyard, originally made of wood beams, were substituted by precast reinforced concrete ones, resting on perimetric curbs, whose cross-section is 0.35x0.30m at the portico and 0.70x0.30m at the loggia.

The portico: (a) detail of portico colonnade (ground floor); (b) ground floor plan of the courtyard.

The loggia: (a) detail of loggia colonnade (first floor); (b) first floor plan of the courtyard.
The connections between floors are guaranteed by an original ancient staircase (Fig. 8) that has been preserved in time, so that last restoration was limited to consolidation of the vaults and steps [5].
2.2. Renovation and Consolidation Works
Up to ‘70s building restoration and structural consolidation were made directly by "SoprintendenzaaiBeniCulturali e Ambientali" (Superintendence of Cultural and Environmental Heritage) consisting in masonry blocks replacements and realization of new reinforced concrete slabs and curbs [6]. In 1994 a significant renovation and consolidation works were conducted, especially on the arcaded courtyard. The building showed cracks, masonry wall disconnections, moisture phenomena, and plaster detachments most of which due to natural elements deterioration and lack of appropriate maintenance [7]. In the 2000s University of Palermo planned a development program for the monumental building of Steri, in order to realize an integrated museum tour and make all its spaces available to the community. This project required a series of urgent maintenance of some areas of the building, such as the arcaded courtyardof the palace, very important in the new organization of the exhibition route, and the sixteenth century stone staircase, in the northern facade of the building [8].

The terrace (a) view of courtyard terrace (second floor); (b) second floor plan of the courtyard.

Original ancient staircase that connects the building floors.
The ground floor walls of the courtyard were, once again, widely affected by rising moisture. Also the plaster, showing efflorescence and cracks, required further improvement, especially in light of the importance of courtyard in the new organization of the exhibition route. Electro-physical dehumidification of masonry was performed through the application of electromagnetic devices [9] and the plaster at the bottom of walls was substituted using a macroporous material having characteristics similar to the removed one. In 2014 the University of Palermo went on the restoration of the facades facing the portico and the loggia of the inner courtyard and its colonnade. Also irregular masonry walls of loggia and reinforced concrete curbs were consolidated, as shown in Fig. (11) and Fig. (12). During works a detailed laser scanner survey revealed potential instabilities of colonnade due to some ruined capitals that were consolidated by micro-nailing.
The courtyard ogival arches rest on columns whose capitals show different appearance and provenance (Fig. 9), as well as evident signs of the many changes that affected the courtyard over the centuries: superstructures, now decommissioned, were added in the portico and also in the loggia (Fig. 10), altering the original architectural line [10].

Example of column capitals: (a) portico calcarenite capital; (b) loggia marble capital; (c) location within the courtyard.

Superstructure occluding portico arches before restoration.

Consolidation of irregular masonry walls of loggia.

Consolidation works on reinforced concrete curbs.
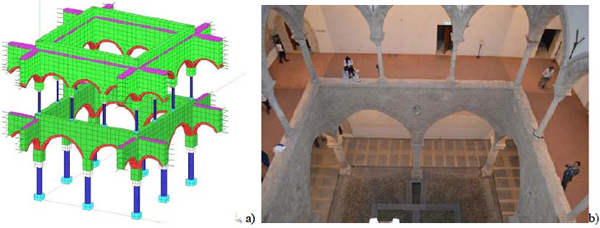
The courtyard: (a) isometric view of F.E. Model; (b) real view of courtyard.
3. A SIMPLIFIED FINITE ELEMENT MODEL
3.1. Model Description
To preserve the historical and architectural uniqueness of Chiaramonte Palace (Fig. 13b), in a relevant seismic area as Italy, dynamic field tests are planned in order to identify its characteristics, calibrate a numerical model and, eventually, evaluate structural vulnerability.This procedure starts from the construction of an initial Finite Element (F.E.) model that is firstly used to select a proper test set-up and then calibrated on the basis of experimentally identified structural modal parameters.To this aim a three dimensional symmetric F.E.model (Fig. 13a) was constructed based on geometrical survey and acquired information. Only the courtyard was modelled and one-dimensional spring elements were located on its boundaries to account for coupling with the surrounding part of the building.
Shell elements were used for masonry walls while columns were modelled using circular cross-section beam elements, whose geometrical properties were taken at the midsection of the element [11, 12]. Also masonry arches and reinforced concrete curbs at each floor were discretized using uniform prismatic cross-section beam elements. Rigid links were introduced to connect adjacent arches to the capital of columns and rigid plane constrains were applied to account for concrete floor slabs.
Material physical and mechanical properties were obtained from standards defined by Italian design codes [13, 14]. Specifically, as for masonry elements it concerns, the ranges reported in Table 1 are recommended.
Recommended range of mechanical and physical properties of structural masonry.
| Material | E (MPa) | G (MPa) | p (kN/m3) |
|---|---|---|---|
| Compact blocksmasonry | 1500-1980 | 500-600 | 21 |
| Irregularmasonry | 690-1050 | 230-350 | 19 |
However, as a consequence of recently done structural restoration, masonry walls and arches reveal a very good appearance. As in fact the restoration project included strengthening of irregular masonry using mortar injections as well as reinforcing steel bars. Also compact block masonry was improved by hollow mortar joints sealing.
To take into account such an improvement of masonry mechanical characteristics, as also suggested by design codes, mean values of Young and Shear moduli (E and G, respectively) where amplified by correction factors so that values reported in Table 2 were finally adopted for the F.E. model.
Mechanical and physical properties of F.E model materials.
| Material | E (MPa) | G (MPa) | p (kN/m3) |
|---|---|---|---|
| Compact blocksmasonry | 1.3x1740=2262 | 1.3x550=715 | 21 |
| Irregularmasonry | 2.0x870=1740 | 2.0x290=580 | 19 |
| Marble columns | 35000 | 14500 | 27 |
| Concrete curbs | 30000 | 12500 | 25 |
Floor dead load of 4500 N/m2 was distributed over beam modelling concrete curbs.
3.2. Calibration Procedure
The stiffness of spring elements at the boundaries of the model are the unknown variables to be determined through a proper calibration procedure. To this aim an estimation of fundamental vibration period of the whole building is firstly obtained. A traditional simplified form relates the period to the structure height H as:
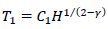 |
(1) |
It can be shown [15] that expression (1) is obtained using Rayleigh’s method, by assuming that along the height of the building: seismic forces (i) as well as deformations (ii) are linearly distributed, mass are constant distributed and, finally, base shear force is proportional to 1/Tγ. Uniform Building Code [16] proposed a value of γ =2/3, i.e.
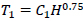 |
(2) |
Eq. (2) is adopted by Italian design codes and EC8 [17] as well, providing different values of C1 depending on structural type. However the case of shear walls masonry structures is not specifically treated by Italian codes, that simply suggest a generic value C1 =0.05, where as EC8 proposes the following expression:
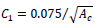 |
(3) |
where:
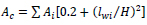 |
(4) |
and:
Ac is the total effective area of shear walls at first floor of the building in m2;
Ai is effective area of the i-th shear wall at first floor of the building in m2;
H is the height of the building from foundation in m;
lwi is the length of the i-th shear wall at first floor of the building, parallel to the applied forces, in m, under the condition lwi/H<0.9.
Using available plans from the restoration project, an approximate value of Ac =26 m2 is obtained, therefore Eq. (3) and Eq. (2), for H = 19.5m, lead to C1 = 0.015 and T1 = 0.14 sec.
It is worth underscoring that using Italian codes the estimation of fundamental period yields T1 = 0.46sec, very different from the value obtained using EC8 that indicates a much stiffer structure. In the following a mean value of T1 = 0.30 sec will be considered as estimation of the fundamental period. The stiffness of spring elements will bedefined using such a value as calibration parameter.
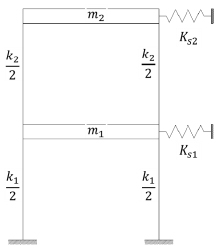
Shear-type frame reduced model.
To this aim numerical model is further simplified and reduced to a one dimensional two stores shear-type frame, connected to external springs at each store as reported in Fig. (14), where m1 = 446.5 Ns2/mm, m2 = 386.0 Ns2/mm, k1= 15183 N/mm and k2 = 43280 N/mm are mass and stiffness values calculated from the F.E. model without boundary springs, while KS1 and KS2 are resulting stiffness of boundary springs. The eigen problem for such a system is written in matrix form as:
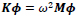 |
(5) |
Where:
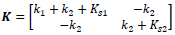 |
(6) |
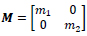 |
(7) |
ω2 is the eigenvalue (modal frequency) and φ is the system eigenvector (mode shape).
Eq. (5) is rewritten for ω21 and φ1 = [φ11 φ12]T leading to:
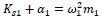 |
(8a) |
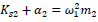 |
(8b) |
where:
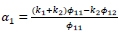 |
(9a) |
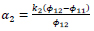 |
(9b) |
Dividing Eq. (8b) by (8a) yields:
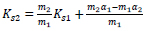 |
(10) |
Constant stiffness values ks1 and ks2 are assumed for all spring elements of the same storey, i.e.
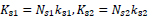 |
(11) |
being Ns1 =40 and Ns2 =64 the total number of spring elements at first and second storey, thus substituting Eqs. (9) and (11) in (10) leads to:
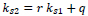 |
(12) |
where:
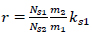 |
(13a) |
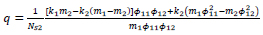 |
(13b) |
Eq. (12) is formally a relationship between ks1 and ks2, but ϕ11 = ϕ11(ks1,ks2) and ϕ12 = ϕ12(ks1,ks2) and q = q(ks1,ks2) therefore, in general, it is not an explicit form.
However, it is reasonable to think that dynamic of the surrounding structure, whose stiffness is certainly larger than the inner courtyard one, dominates the entire structural behavior. From the geometrical survey, its mass and stiffness properties are not expected to change significantly along the height, therefore if it also vibrates as a two store shear-type frame, with constant stiffness and mass distribution, first normalized mode shape is mass and stiffness independent and given by:
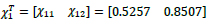 |
(14) |
In the following, it is assumed that inner-courtyard first mode shape is equal to surrounding structure one, that is:
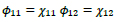 |
(15) |
that, combined with Eqs. (12) and (13), reduces the calibration problem to a single variable one, i.e. k = ks1.
Thus the following objective function is established:
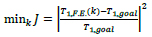 |
(16) |
and minimized to obtain the optimal value of k, under the condition k ≥ − q/r. In Eq. (16) T1.goal =0.30 sec and T1.F.E(k) is first F.E. model vibration period. In Fig. (15) the logJ(k) function is reported; numerical minimization leaded to ks1 = k =8300 N/mm and, therefore, ks2 =4070N/mm. In Table 3 first 6 modal frequencies and corresponding effective relative modal masses are reported. The effective relative modal mass associated to the k-th mode is defined as:
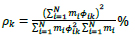 |
(17) |
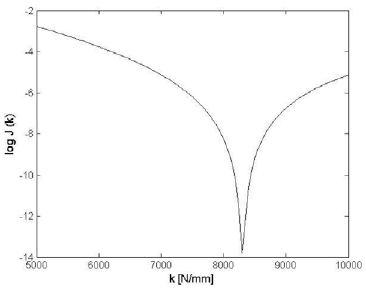
Objective function.
Calibrated F.E. model dynamic characteristics.
| Mode n. | T (sec) | ƒ (Hz) | ρx (%) | ρy (%) |
|---|---|---|---|---|
| 1 | 0,300 | 3,333 | 0,05 | 75,43 |
| 2 | 0,299 | 3,341 | 75,84 | 0,05 |
| 3 | 0,229 | 4,364 | 0,01 | 0,03 |
| 4 | 0,227 | 4,399 | 21,38 | 0,68 |
| 5 | 0,227 | 4,402 | 0,68 | 21,74 |
| 6 | 0,180 | 5,559 | 0,00 | 0,00 |
where N is the number of the degrees of freedom, mi are the component of the diagonalized system mass matrix, so that Mtot = ΣNi=1mi, and ϕi is the i-th component of the k-th eigenvector. Eq. (17) is projected along the coordinate system to obtain x-, y- and z-axis effective relative modal mass associated to each mode.
As expected, due structural symmetry, mode 1 and 2 and mode 4 and 5show very close frequencies and they represent first two flexural modes along x- and y-axis, while mode 3 and 6 are torsional ones.It is also worth to notice that first five modes activate more the 95% of modal mass and, between them, first twoare clearly predominant for seismic behavior characterization. In Fig. (16) structural mode shapes are reported; symmetric modes are not included.
3.3. Experimental Set-Up Planning
Results of such a F.E. model can be used to definite equipment and set-up for an ambient vibration test campaign, whose goal will be the dynamic characterization of the structure. According to numerical results, the system dynamic should be fully defined in the frequency range of 0-6 Hz, thus a sampling frequency of 100Hz, that is more than 10 times the expected significant frequency content, will be sufficient to get a good time signal resolution and avoid aliasing phenomena. Sensors frequency range must also be selected by taking into account the estimated system frequencies and their measuring resolution must be appropriate to micro-tremors vibration level.Moreover, F.E. model mode shapes provide information regarding sensor locations; as in fact they are useful to avoid mode shape nodes and to obtain a good spatial representation of system dynamic response, compatibly with the number of available sensors.
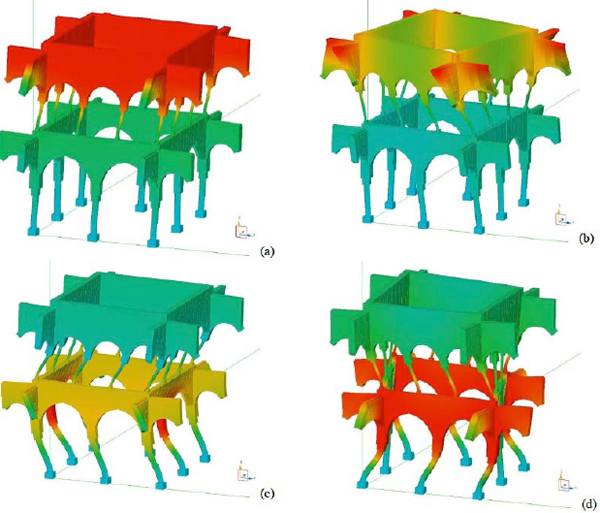
Modal shapes of F.E. model of the courtyard: (a) mode num 1; (b) mode num3; (c) mode num 4; (d) mode num 6.
CONCLUSION
Chiaramonte Palace is a wonderful example of the historical heritage in Palermo. The inner courtyard, characterized by its magnificent dual arcade, is the dominant architectural element of the building. Such an architectural element appears often in buildings of historical heritage and, especially under seismic excitation, it represents the most vulnerable structural part. To preserve the historical and architectural uniqueness of the building, in a relevant seismic area as Sicily, dynamic tests are going to be performed to identify its characteristics, calibrate a numerical model and, eventually, evaluate the structural vulnerability. This procedure requires, first of all, the construction of a proper F.E. model to be used for a valid test set-up definition. A simplified numerical model of the courtyard is proposed, based on geometric survey and standard material properties provided by design codes. One-dimensional spring elements are placed on its boundaries to account for coupling with the surrounding part of the building. Stiffness of such a spring elements were calibrated, after some assumptions, by minimizing a one-variables objective function defined on the basis of the estimated fundamental period. The results of calibrated F.E. model pointed out that first two modes (translational) are predominant over the structural seismic behavior. The expected significant frequency range of the structural dynamic response was identified and used to define the investigation range for the experimental tests. Moreover F.E. model mode shapes provided fundamental information for sensor locations.The proposed modeling procedure does not affect the reliability of the results and, as shown, it can be usefully applied to theoretical and experimental dynamic characterization of existing buildings with inner courtyards.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTs
Declared none.


