All published articles of this journal are available on ScienceDirect.
Seismic Design of Box-Type Unreinforced Masonry Buildings Through Direct Displacement-Based Approach
Abstract
In the last decade, displacement-based seismic design procedures have been recognised to be effective alternatives to force-based design (FBD) methods. Indeed, displacement based design (DBD) may allow the structural engineer to get more realistic predictions of local and global deformations of the structure, and hence damage, under design earthquakes. This facilitates the achievement of performance objectives and loss mitigation in the lifetime of the structure. Nonetheless, DBD needs further investigation for some structural types such as masonry buildings.
In this paper, a direct displacement based design (DDBD) procedure for unreinforced masonry (URM) buildings is presented and critically compared to FBD. The procedure is proposed for box-type URM buildings with reinforced concrete slabs, bond beams and lintels above openings, which have shown acceptable seismic performance in severe earthquakes preventing out-of-plane failure modes. Seismic design of a three storey brick masonry building in a high seismicity region is discussed as a case study. The effects of ordinary and near-field design earthquakes, as well as load combinations and accidental eccentricity prescribed by current codes, were investigated. Finally, design solutions provided by FBD and DDBD were optimised and their construction costs were estimated. It was found that, particularly at small epicentral distances, neglecting the combination of horizontal seismic actions and accidental eccentricity may induce significant underestimation and an ideally more uniform distribution of strength demands on URM walls. In addition, construction costs resulting from DDBD may be significantly lower than those related to code based FBD procedures.
1. INTRODUCTION
In recent years, seismic design codes have been significantly revised to address the main concepts of performance-based earthquake engineering (PBEE). This new philosophy allows engineers to better work with stakeholders, such as facility managers, owners, and insurers, in identifying the most probable performance of structures under earthquakes [1]. In case of new facilities, performance based design (PBD) aims at achieving predefined performance objectives when the structure is subjected to a design earthquake associated with a prescribed level of seismic hazard. Multiple performance objectives are then considered, including damage control in minor earthquakes, life safety in moderate earthquakes, and collapse prevention in major earthquakes [2]. A key issue is how to predict seismic performance, damage and losses in the lifetime of the structure. This needs an accurate modelling of seismic hazard and capacity, as well as a realistic simulation of demand on structural and non-structural components. Theoretical and experimental studies have shown that deformations rather than forces are typically a good proxy of seismic damage, delineating drifts as engineering demand parameters well correlated with losses. To account for this consideration, in the 1970’s and 1980’s, earlier force based design (FBD) procedures dating back to the 1930’s were improved by introducing the concepts of ductility and strength reduction factor. Nevertheless, a part of research community recognises that current FBD procedures fail in some important assumptions and are based on safety verifications in terms of internal forces, shifting displacement checks to the final stage of the design process. Displacement based seismic design procedures have thus received great interest from the 1990’s, as they are more effective than FBD approaches in predicting/controlling both local and global deformations of structures [3-5]. For instance, distributing earthquake resistance throughout the structure on the basis of equilibrium considerations instead of stiffness based formulations typically produces a more controlled and predictable seismic response, avoiding undesirable failure modes.
Priestley et al. [6] developed a direct displacement based design (DDBD) methodology which was specialised to different types of structures accounting for their specific behavioural features. DDBD allows one to design the structure so that the overall displacement demand corresponding to a given design earthquake does not exceed displacement capacity, the latter depending on materials and structural configuration. More recently, a model code for DDBD implementation and use by professional engineers was proposed [7].
Few studies have been carried out on seismic design of masonry buildings through the DDBD approach. This is urgently needed because masonry is still used to build new structures in earthquake prone regions [8]. A displacement based approach was proposed by Calvi [9] but it applies to seismic vulnerability assessment of existing masonry buildings at regional scale. In case of reinforced masonry buildings, a DDBD procedure was developed and validated through shaking table tests [10, 11]. In this paper, the DDBD approach is specialised to unreinforced masonry (URM) buildings at site-specific scale. It is assumed that proper detailing is adopted to prevent out of plane failure modes to masonry walls, so that each wall is laterally loaded in its own plane contributing to the global earthquake resistance to the building. After that FBD is critically reviewed, a DDBD procedure is set up and is applied to a three storey URM building located in a site with high seismic hazard. Effects of load combinations and accidental eccentricity considered by current seismic codes are assessed and discussed. Finally, construction cost estimates associated with design solutions of FBD and DDBD are compared.
2. FUNDAMENTALS AND DRAWBACKS OF FORCE-BASED DESIGN OF UNREINFORCED MASONRY BUILDINGS
The majority of modern seismic codes allows engineers to design URM buildings according to the FBD approach. This is the case of, amongst others, European codes such as Eurocode 8 (EC8) - Part 1 [12] and the 2008 Italian Building Code (IBC) [13] where the same FBD framework is adopted. To really detect the main limitations of that design approach as applied to masonry buildings, the FBD assumptions are briefly reviewed in the following, making reference to the aforementioned building codes.
2.1. Force-Based Design Procedure
The definition of seismic input on the structure is the first step of any seismic design procedure. In case of FBD, seismic action on structures is defined through acceleration response spectra. In EC8-Part 1 which applies to buildings, spectral shapes for both horizontal and vertical components of seismic action are provided. Two spectral shapes are defined, depending on whether the earthquake that mostly contributes to seismic hazard at a given site has surface magnitude lower than 5.5 or not. The functional form of all spectral shapes basically depends on the design ground acceleration ag, which is related to the seismic classification of territory or seismic hazard maps in each country.
EC8 spectra are related to seismicity through only ag. This relationship is enhanced into IBC [13] where the influence of seismic hazard at the site on elastic response spectra is directly considered, based on a probabilistic seismic hazard analysis (PSHA) by the Italian National Institute of Geophysics and Volcanology (INGV) [14]. PSHA provided hazard curves in terms of ag and spectral acceleration for ten periods of vibration (T = 0.1-2 s) and each node of a regular grid having 5 km spacing and covering the whole Italian territory with 10,751 nodes [15]. Those hazard curves were lumped in nine probabilities of exceedance in 50 years (from 2% to 81%) for seismic design/assessment purposes. Based on PSHA results, IBC provides site dependent response spectra defined by ag and two additional hazard parameters, as follows: Fo = maximum amplification factor of horizontal spectral acceleration, and TC* = upper bound period of the constant spectral acceleration branch on type A ground (i.e. rock or rock like geological formation). It is noted that EC8-Part 1 [12] sets Fo = 2.5 because it does not account for the influence of deep geology on seismic hazard. In that way, IBC allows engineers to design structures through design spectra with the same functional form as in EC8, but with ordinates that are very close to those of uniform hazard spectra (UHS) for each site. By definition, the UHS is a response spectrum associated with a probability PVR of exceeding a prescribed level of intensity measure (IM) in a given reference (temporal) period VR and geographical location. In case of IBC, ag is chosen as IM and VR is defined by accounting for the importance and use of the structure, and hence the impact of its collapse on losses, in due consideration. The return period of the design earthquake TR is then derived from PVR and VR by assuming a homogeneous Poisson’s stochastic process for earthquakes. Different PVR-values are set up to account for the limit state of interest according to PBD [1]. Besides, different VR-values are considered to ensure reliability differentiation according to CEN [16], equivalently to EC8-Part 1 provisions where seismic action is amplified by an importance factor γI. IBC provides VR = VN CU where: VN = nominal lifetime of the structure, and CU = importance factor of the structure. To account for ground motion amplification effects due to local site conditions, peak ground acceleration is defined as PGA = agS where S is a soil factor derived as a stratigraphic amplification factor (SS) times a topographic amplification factor (ST). It is emphasised that EC8-Part 1 accounts for topographic amplification effects only in case of important structures, assuming γI > 1. Stratigraphic conditions are also considered into IBC [13] when defining the limit periods of the elastic response spectra. Indeed, a soil related factor CC is used and multiplied by TC* to define TC (namely, the upper bound period for soils different from type A) and to derive other limit periods denoted by TB and TD.
Dealing with seismic demand, an equivalent (viscous) damping ratio equal to 5% and a first mode vibration period T1 are assumed for a building. If the URM building has a rather uniform mass distribution along the height, the designer may set T1 = 0.05H3/4 where H is the building height. Alternative period formulations are provided by EC8–Part 1 [12]. Then, the horizontal acceleration demand Sa(T1) at the base of the building is estimated through the elastic response spectrum. The design acceleration demand at ULS is defined as Sd(T1) = Sa(T1)/q, where q is the strength reduction factor (or behaviour factor) of the building. EC8–Part 1 provides q = 1.5–2.5 for seismic design of URM buildings. IBC provides the behaviour factor as q = q0 KR where: q0 = maximum strength reduction factor associated with presumed ductility and overstrength levels in the structure, and KR = reduction factor related to building irregularity along the height. In case of URM buildings, IBC provides q0 = 2αu/α1 where: α1 = horizontal load multiplier corresponding to the lateral strength of the weakest wall, αu = 90% of the horizontal load multiplier corresponding to the peak base shear resistance of the building, and αu/α1 = system overstrength factor assumed to be 1.4 and 1.8 for single storey and multi-storey URM buildings, respectively. In case of in plan irregular URM buildings, IBC allows the designer to set αu/α1 as average of the value recommended for in plan regular buildings and unity.
After that the inertia mass of the building is estimated, the design base shear may be computed and vertically distributed according to the tributary inertia masses of floors and first mode displacement profile. That profile is typically assumed to be linear for URM buildings. The horizontal force at each floor level is applied to the centre of mass CM and distributed among URM walls in proportion to their lateral stiffness. To account for spatial variation of seismic ground motion and uncertainty in the location of inertia masses, an accidental eccentricity ea ≥ ±0.05L is assigned to the nominal location of CM where L is the floor dimension perpendicular to the direction of seismic action. Accidental eccentricity is supposed to have the same magnitude and sign at any floor level. Furthermore, the effects of horizontal seismic components along two perpendicular directions are combined considering a factor equal to ±1 and ±0.3 for the primary and secondary action, respectively.
Based on linear structural analysis, safety checks in terms of strength are performed on each structural component of the URM building. In case of box type URM buildings, the capacity model is a three-dimensional (3D) system of load-bearing walls connected each other by masonry interlocking at wall intersections in plan, reinforced concrete (RC) bond beams or other tying elements at each floor level, and RC floor slabs assumed to be rigid diaphragms. URM walls with openings are typically modelled according to the macro element approach or equivalent frame idealisation [17]. Each load bearing wall is a system of Timoshenko beam elements which are named 'macro-elements' as they have a size comparable to that of openings. It is worth noting that capacity design is not allowed in case of URM buildings, because shear and bending capacities cannot be independently modified without changing the aspect ratios of structural elements. This implies a completely different approach to URM buildings compared to other structures such as RC and steel frames, where capacity design establishes a strength hierarchy among structural components. According to the load resistance factor design (LRFD), structural safety is assumed to be met if strength demand does not exceed the factored capacity. On the deformation side, linear seismic analysis does not directly provide inelastic displacement demands on macro elements. Those demands are estimated as elastic displacements multiplied by a displacement amplification factor µd associated with q, T1 and TC. If the displacement demand to capacity (DCR) ratio exceeds unity, the size of load bearing walls should be modified and the FBD procedure should be repeated until DCR ≤ 1 is reached in any wall. Nevertheless, displacement checks may be avoided if detailing rules are applied.
2.2. Force-Based Design Limitations
Force-based design of URM buildings is affected by several major drawbacks. First of all, the first mode period of vibration is assumed to be independent of the actual 3D configuration and lateral stiffness of the structural system. This assumption may significantly influence seismic demand, and hence the actual reliability level resulting from safety checks.
Secondly, the q-factor of the structure is assumed to be independent of T1, opposed to research findings for short-period structures (see e.g. [18]). Low energy dissipation levels in URM buildings with significant rocking behaviour of load-bearing walls should also be considered when assuming the q-factor. In fact, that type of hysteretic behaviour under in plane lateral loads is associated with large displacements and pseudo ductility on one hand, and with thin cycles that cause rather low equivalent damping ratios [19] on the other hand. In addition, αu/α1 should be defined on the basis of the actual structural configuration. In this respect, a large (statistically sufficient) number of non linear analyses of capacity models representative of the main URM building classes is still needed.
Finally, an important design limitation comes from the assumption of lateral stiffness for each load-bearing wall, which is supposed to be independent of the lateral strength of walls. In line of principle, lateral stiffness should be set different from initial stiffness as a result of masonry cracking. This is recognised by EC8-Part 1 [12] and IBC [13] as well. Nevertheless, in absence of an accurate evaluation of bending and shear stiffness of macro elements, those codes allow the cracked lateral stiffness to be set up to 50% of the elastic stiffness regardless of the axial load level and masonry type. Non-linear moment curvature analysis results have shown that both the bending curvature at masonry early crushing and curvature ductility of an URM cross section significantly depend on the axial load magnitude, drastically affecting lateral strength and stiffness of the whole macro-element [20]. It is stressed that: (1) wrong assumptions for lateral stiffness may result in unlikely distributions of seismic demand on walls, as shown by non-linear numerical simulations of laterally loaded masonry walls [21]; and (2) the stiffness based distribution of seismic floor forces according to FBD induces strength demand concentrations on stiffer macro elements, resulting in an available displacement ductility of the structure which may be notably lower than that associated with the assumed value of behaviour factor.
Stiffness-related problems may be partially overcome if lateral stiffness of URM walls is iteratively determined on the basis of the actual strength demand on macro elements, provided that force–displacement diagrams are considered [22]. Nonetheless, even if a trial and error stiffness estimation procedure is employed to compute the secant lateral stiffness corresponding to strength demand on each macro element, FBD limitations regarding the vibration period and strength reduction factor still remain unsolved. Typically, this does not result in an optimal structural design solution for the URM building, strongly reducing the ability of predicting the actual inelastic seismic response.
3. DIRECT DISPLACEMENT-BASED DESIGN PROCEDURE FOR UNREINFORCED MASONRY BUILDINGS
In this section, a seismic design procedure according to the general DDBD framework [6] is presented and specialised to URM buildings in compliance with EC8-Part 1 [12] and IBC [13], the latter regarded as EC8-like code. The design procedure consists of the following steps.
Step 1: Define the Building Features
Based on current code rules at both national and international levels [12, 13], URM buildings should be composed of load bearing walls with proper masonry interlocking at their intersections, lintels above openings, and (RC) bond beams at each floor level. Floor systems should have sufficient in plane stiffness and strength with proper connection to masonry walls, in order to distribute horizontal seismic actions in plan. If these provisions are met, the URM building is likely to experience a box type global seismic response which activates the in plane capacity of load-bearing walls. Geometric limitations for walls and RC bond beams, as well as the type and minimum strength of masonry and reinforcement, are provided by codes. Nonetheless, the structural geometry also depends on architectural choices and expected costs.
Step 2: Develop a Macro-Element Capacity Model of the Structure
The seismic capacity model of the URM building is developed through a macro-element idealisation of load-bearing walls with openings [22]. Horizontal and vertical masonry strips between consecutive opening series identify spandrels and piers, respectively (Fig. 1). Spandrel pier intersections define joint panels, which are assumed to be rigid. Conversely, two types of flexible macro elements are defined: (1) pier panels, namely vertical macro-elements which are geometrically defined as fraction of piers between two consecutive spandrels and openings, and (2) spandrel panels, namely horizontal macro-elements which are geometrically defined as fraction of spandrels between two consecutive piers and openings.
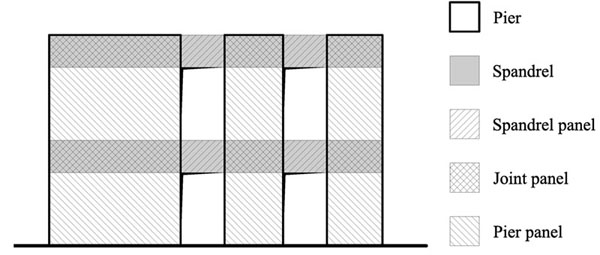
Macro-element idealisation of load-bearing URM wall with openings.
Both pier and spandrel panels may fail in bending or shear, depending on their size, boundary conditions and masonry properties, i.e. strength and ultimate strain. Several formulations allow one to predict the in plane lateral strength of macro elements ([17, 22]). To define the ultimate drift capacity θu, two alternative approaches may be used. The former is a mechanical method of non-linear analysis where the force displacement diagram of the macro-element subjected to in plane lateral loading is derived by direct integration of axial and shear strains, according to the macroscopic constitutive model assumed for the masonry and the axial load produced by gravity loads. In the second approach, a multi linear phenomenological force displacement diagram is defined where drift capacity is assumed according to experimental evidence and code provisions. In that case, two different capacity limits are set up depending on the expected type of in plane lateral response for the macro-element. If a flexure dominated macro element is concerned, EC8-Part 3 [23] allows one to assume θu = 4/3θSD,f l 0/d where: θSD,f = drift capacity corresponding to the significant damage limit state for flexural failure, which is set to 0.008; l 0 = distance between the section where flexural capacity is attained and the contraflexure point; and d = cross section depth of the macro element. As l 0 depends on the boundary conditions of the macro element, it may be assumed to range between 0.5l (doubly-fixed macro-element) and l (cantilevered macro element), where l is the macro-element length. If a shear dominated macro element is considered, the ultimate drift capacity is defined as θu = 4/3θSD,s where θSD,s = drift capacity corresponding to the significant damage limit state for shear failure, which is set to 0.004. Different drift capacity levels are provided by IBC [13] where θu = 0.008 in case of flexural failure (reduced to 0.006 when dealing with existing buildings) and θu = 0.004 in case of shear failure. It is emphasised that flexural failure is associated with masonry crushing at macro-element toes, whereas shear failure is typically determined by diagonal tension cracking or diagonal shear sliding. Indeed, the assumption of an ultimate drift associated with bed joint sliding would make no practical meaning because it would be significantly larger than that related to other failure modes. Direct shear tests on masonry specimens have shown that bed-joint sliding is associated with high energy dissipation and very large deformations [24, 25]. In a design framework, this means that the ultimate drift associated with bed joint sliding would be so high that the actual drift capacity of the macro-element would be related to other failure modes.
In addition to drift capacity, the equivalent damping ratio ξe is a key design parameter to be defined as it quantifies the energy dissipation capacity of the structure. When a FBD procedure is used, the elastic spectral acceleration is estimated by considering only the elastic fraction of damping, which is measured by the equivalent damping ratio ξel associated with elastic behaviour. The latter is typically set to 5% but higher values may be assumed in specific cases to account for the influence of damping on the elastic response spectrum. Conversely, in the DDBD approach, the equivalent damping ratio is used to measure the total energy dissipation capacity so it is assumed to be ξe = ξel + ξhys where ξhys is the equivalent damping ratio associated with hysteretic behaviour. Scaling down the system of interest from the overall building structure to a single macro element, it may be assumed that ξe depends on the failure mode expected for the macro element [26]. Shear compression tests on clay brick masonry walls have shown that equivalent damping may be associated to rocking or diagonal shear failure modes. Conversely, any assumption of equivalent damping ratio associated with bed joint sliding (even higher than 60% if an elastic-perfectly plastic behaviour is assumed) would not be conservative because of the high energy dissipation corresponding to that failure mode. A flexure dominated macro element has a very low energy dissipation capacity, resulting in ξhys = 5% and even lower damping ratios in case of URM walls with masonry arches above openings [19]. In case of shear dominated macro-element, the hysteretic response is characterised by higher energy dissipation, resulting in ξhys = 10%. If the elastic damping ratio is set to 5%, ξe turns out to be 10% and 15% in case of flexural and diagonal shear failure, respectively. Radiation damping associated with rocking response is generally small so it may be neglected in seismic design of URM buildings.
Step 3: Assume a Global Collapse Mechanism for URM Walls
Shear failure of piers induces not only a low displacement capacity but also the potential occurrence of soft storey mechanisms of load bearing walls. Rocking is thus the preferable type of in plane lateral behaviour for piers because it allows a global collapse mechanism to develop. Rocking of piers takes place if spandrels suffer damage. Rocking behaviour is characterised by a sort of rigid body rotation around pier toes which results from tensile cracking of masonry under lateral loading, contributing most part of lateral drift compared to that associated with bending and shear deformations. Based on numerical simulations of in plane lateral loading tests on URM walls with single opening, Parisi et al. [21] validated the following equation for prediction of drift demand on spandrels:
 |
(1) |
where: θS = drift demand on spandrel panel; θP = drift demand on pier panel; lP = length of pier panel; and lS = length of spandrel panel (Fig. 2a). According to Eq. (1), the drift demand on spandrels is larger than that on piers. The target (design) drift θd is set equal to the pier drift θP whereas a design assumption concerning the effectiveness of spandrels in providing a coupling action on piers must be made. To that end, spandrels may be supposed to be coupling elements if their length is sufficiently larger than pier length. An acceptable hypothesis may be to assume coupling spandrels if θS ≤ 1.5 θd. In case of piers and spandrels with different lengths, Eq. (1) may be generalised to:
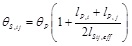 |
(2) |
where: i, j = consecutive piers; and lSij,eff = effective length of spandrel panel between piers i and j. That effective length accounts for curvature penetration within piers and depends on the spandrel sectional depth hSij. From a design viewpoint, the effective length of spandrel panel may be assumed to be lSij,eff = lSij + 2hSij. Therefore, after that the design drift is assigned to the pier, the rotation demand on the spandrel may be predicted assuming that it is uniformly distributed over the building height.
Step 4: Check Pier Coupling Provided by Spandrels at Each Floor Level
When a load bearing URM wall with openings is laterally loaded in its own plane, spandrels play a key role as they may provide significant coupling between piers. The coupling action depends on: (1) the spandrel type, namely URM spandrel with no tensile resistant elements, composite RC-URM spandrel with RC bond beam, or URM spandrel with floor slab; (2) geometric conditions such as those into Eqs. (1) and (2); and (3) force equilibrium conditions. Based on chord rotation demand provided by Eq. (1) or (2), the bending moment transmitted by spandrels to piers may be predicted through the moment rotation relationship assumed for spandrels (Fig. 2b). If the spandrel includes a RC bond beam or floor slab, the yielding rotation of the spandrel panel may be computed by considering 10% contribution from shear deformation, as follows [6]:
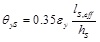 |
(3) |
where: εy = yielding strain of reinforcing steel; lS,eff = effective length of the spandrel panel; and hS = spandrel height. If an elastic perfectly plastic (EPP) moment rotation diagram is assumed, the bending moment transmitted by the spandrel to the pier is MS = MuSθS/θyS if θS < θys and MS = MuS if θS ≥ θyS.
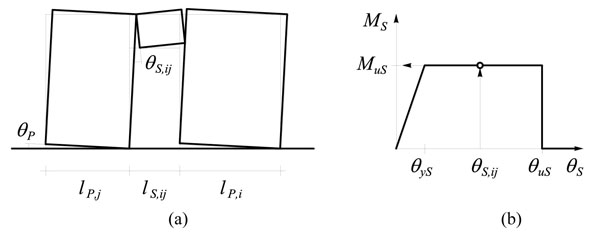
Demands on spandrel panel: (a) drift demand; (b) bending moment demand.
If the spandrel includes a floor slab, the bending moment may be calculated assuming that the effective width of the floor slab is three times the thickness of the supporting wall.
The coupling action provided by spandrels may be measured by the coupling ratio, namely the fraction of overturning moment carried by spandrels and defined as follows:
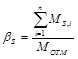 |
(4) |
where: MS,k = bending moment transmitted by spandrels to piers at the i-th floor level; and MOTM = overturning moment given by the sum of resisting moments at the base of piers and bending moments transmitted by spandrels.
The bending and shear forces transmitted by coupling elements may increase the lateral resistance of the building, producing additional damping, increasing the stiffness of load bearing walls, and changing the contraflexure height Hcf. Nonetheless, in case of URM walls with openings, the coupling degree is not completely a design choice as it mainly depends on the characteristics of floor slabs and RC bond beams.
The maximum level of coupling depends on the balance between flexural and shear strengths of spandrels and vertical loads carried by piers and spandrels. The shear forces corresponding to the bending moments of spandrels may be computed through equilibrium equations, so the actual coupling degree must be compatible with the following equilibrium condition at each floor level (Fig. 3a):
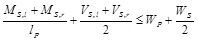 |
(5) |
where: MS,l, MS,r = bending moments on left and right sections of spandrel panel; VS,l, VS,r = shear forces on left and right sections of spandrel panel; and WP, WS = vertical loads acting on pier and spandrel panels, including self weight and tributary loads transferred by the floor. It is noted that the maximum transmittable shear force is simply equal to the sum of ultimate moments divided by the span length.
If Eq. (5) is not met (typical case of upper floor levels), the bending moments and shear forces transmitted by the spandrel are reduced in proportion to the unbalance level and βS is computed through Eq. (4). The coupling action of spandrels induces axial load variations ΔN in piers, which are equal to the shear forces transmitted by spandrels (Fig. 3b). In case of URM walls with openings, it is emphasised that neglecting axial load variations due to lateral actions may not be conservative because those variations may reach large fractions of axial loads due to gravity loads NG [21]. The total axial load at the base of coupled piers is then equal to N = NG ± ΔN where ΔN = ΣVS,i (i = 1,…,n). Axial load variations clearly depend on the combination of horizontal seismic actions.
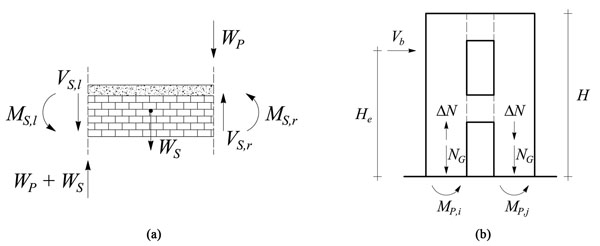
(a) Equilibrium condition for spandrel panel; (b) axial loads in piers.
If the spandrel does not have RC bond beams nor floor slabs, its coupling action is due to the formation of a diagonal strut within the masonry of each spandrel panel. That resisting mechanism is limited by the masonry compressive strength in the direction parallel to bed joints (fmh), namely the horizontal direction of the spandrel. That compressive strength may be notably lower than that in the direction perpendicular to bed joints (fm), i.e. the vertical direction of the spandrel. For instance, the Italian guidelines for strengthening of existing structures with fibre-reinforced polymers [27] assume fmh = 0.5fm. If a strut develops within masonry, Eqs. (4) and (5) still apply.
If the spandrel includes a lintel well bonded to the piers above openings, MS reaches its peak value at the end section of the spandrel panel where the maximum internal lever arm is attained and is almost zero at the opposite end section.
Step 5: Evaluate the Contraflexure and Effective Heights
A displacement profile of the building over the height Δ = [Δ1 ... Δn]T should be assumed to predict the effective height He, that is the height of the equivalent single degree of freedom (SDOF) system for the actual structure. The ratio of the effective height to the building height, i.e. He/H, may be estimated as a function of the number of storeys n. Nonetheless, in case of low rise URM buildings (n = 2-4), one may assume He = 0.8H [6]. It is noted that the target displacement Δd by which the structure is designed is the horizontal displacement Δd,CM at the centre of mass, that is located at He. Besides, the contraflexure height Hcf may be estimated as a function of the coupling ratio βS through the following equation:
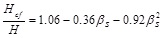 |
(6) |
which was derived by non-linear regression and has a coefficient of determination R2 = 0.975.
Step 6: Check the Assumption of Global Collapse Mechanism and Evaluate the Effective Mass of the Equivalent SDOF System
The shear force Vf corresponding to flexural failure of the spandrel should not exceed the shear force Vs related to diagonal shear failure. If Vf ≤ Vs in all spandrels, the assumption of global collapse mechanism is verified. Otherwise, a soft storey mechanism is expected so the design drift is assumed to be 0.5% or 0.4% according to EC8-Part 3 [23] or IBC [13], respectively.
A displacement profile of the building over the height should be assumed to define the effective mass as follows:
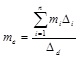 |
(7) |
The displacement profile of the building at maximum response may be governed by the stiff or flexible wall, depending on the ratios between their yielding and plastic rotations. That displacement profile is related to the inelastic fundamental modal shape of the structure. Nevertheless, a linear displacement profile over the building height may be assumed for an URM building which meets both in plan and in elevation regularity rules (see e.g. EC8-Part 1 [12]). That hypothesis allows me to be defined as 90% of the building mass, before that Δd is estimated. Fig. (4) respectively emphasise displacement profiles corresponding to shear (unfavourable) and flexural (favourable) failure of piers in a masonry wall with openings. Even if equal drift capacities are considered, the top displacement related to rocking behaviour of piers is larger than that related to shear dominated behaviour, namely Δnf > Δns.
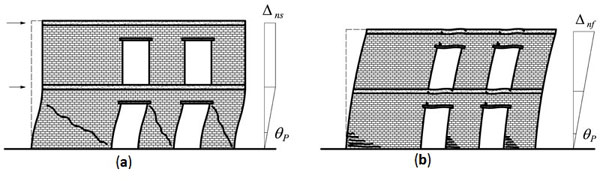
Lateral displacement profile in relation to the expected failure mode of piers in a load-bearing masonry wall with openings: (a) piers failing in shear; (b) piers failing in flexure.
Step 7: Define the Equivalent Damping Ratio of the Building
The equivalent damping ratio ξe is one of the parameters needed to characterise the equivalent SDOF system and clearly depends on the equivalent damping ratios of load bearing walls. Based on this consideration and in the general case of systems composed of m lateral load resisting elements with different lateral strength and damping, ξe may be defined as weighted average based on the energy dissipated by the elements, as follows:
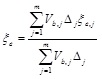 |
(8) |
where: Vb,j = design base shear at the target displacement; Δj = lateral displacement at He; and ξej = equivalent damping ratio of the j-th element (see Step 2). Dealing with URM buildings, if no torsional response is expected, all piers experience the same displacement at He so that Eq. (8) simplifies to:
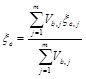 |
(9) |
Priestley et al. [6] suggested to distribute the total base shear between walls (the piers in this case) in proportion to their squared length, providing a rather uniform reinforcement amount in RC or reinforced masonry structures. If this recommendation is applied, Eq. (9) may be rewritten as follows:
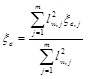 |
(10) |
where lw,j is the length of the j-th pier. If piers are not significantly coupled by spandrels, Eq. (10) provides the equivalent damping ratio of the entire structure without needing the distribution of the base shear between load bearing walls. Furthermore, if a soft storey collapse mechanism is expected for the building (see Step 6), Eq. (10) is not used and ξe may be directly assumed to be 15%. The problem becomes different if piers are coupled by spandrels. In that case, neglecting the coupling action of spandrels would be overly conservative to estimate the equivalent damping ratio of the overall structural system. The coupling ratio of URM buildings is typically βS ≤ 0.5 because of the higher ductility demands on spandrels compared to piers. Assigning a ‘Takeda fat’ hysteretic rule to each spandrel, the equivalent damping ratio of that macro-element may be predicted according to the following ξe–µS relationship:
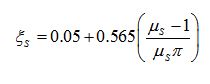 |
(11) |
where µS is the ductility demand on the spandrel, that is µS = 1 if θS ≤ θyS and µS = θS/θyS if θS > θyS. In case of multiple spandrels, Eq. (11) still applies if the average ductility demand on spandrels is considered. As a result, the equivalent damping ratio of an entire URM wall with openings and coupling spandrels may be defined as follows:
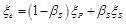 |
(12) |
where ξP is the equivalent damping ratio of piers. If the spandrel strength is not uniform over the building height, Eq. (12) may be written as:
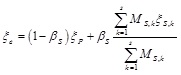 |
(13) |
where: s = total number of spandrels; and ξS,k = damping ratio of the k-th spandrel. Fig. (5) shows the transformation of the actual building structure subjected to lateral forces into the equivalent SDOF system subjected to the design base shear Vb. The SDOF system has effective stiffness ke which is defined as secant lateral stiffness corresponding to the target displacement Δd.
Step 8: Determine the Target Displacement Accounting for Torsional Response of the Structure
If the building structure is expected to experience no torsional response, the target displacement may be directly assumed to be Δd = θPHe. Otherwise, a reduction in the target displacement is induced by torsional rotation. From a design viewpoint, this means that Δd must be properly reduced so that the wall subjected to the maximum displacement demand due to torsional response does not exceed its displacement capacity. The torsional rotation depends on the eccentricity eV between CM and centre of strength CV, whose components in the principal directions of the building plan are:
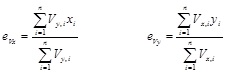 |
(14) |
where Vx,i and Vy,i are the lateral strengths of piers in the x- and y-direction of the building plan, respectively. It is emphasised that URM buildings are torsionally restrained systems, so the lateral strength of piers may be assumed to be known at the beginning of the design procedure. A conservative estimate of torsional stiffness may be derived as follows:
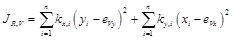 |
(15) |
assuming that every pier fails in flexure and has an effective lateral stiffness proportional to its strength, namely keff,i = Vi/Δd. This is an approximate assumption as it does not account for the torsional response, but it may be accepted if the torsional rotation is reasonably small. This also implies the full inelastic response to occur simultaneously in both principal directions. The torsional rotation demand in each direction of the building plan is then given by:
 |
(16) |
where Vb,x and Vb,y are the design base shear forces in the x- and y-direction, respectively. Finally, the design displacement of CM in each direction may be reduced by the torsionally induced displacement demand on the most external (and hence critical) load bearing wall, that is:
 |
(17) |
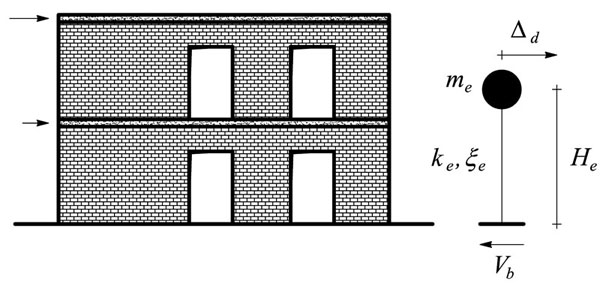
Definition of the equivalent SDOF system.
Thus, Δd,x and Δd,y are associated with the lateral displacements of the critical walls, the torsional rotation θn, and the distances between the critical walls and CV. Opposed to FBD procedures, accidental eccentricity is not typically taken into account in DDBD since it is supposed that this eccentricity induces a uniform increase in strength capacity of all structural elements, resulting in torsional moment amplification and minor effects such as reduction in displacements [6]. Nonetheless, global and local effects of accidental eccentricity on the DDBD solution of a case-study URM building are assessed in Sect. 4 of this paper.
Step 9: Define the Design Earthquake Through Seismic Hazard Disaggregation
In order to assess the design earthquakes that provide the highest contribution to the probability of exceeding a prescribed PGA level in the reference period VR, seismic hazard at the site is disaggregated in terms of source to site distance R and moment magnitude Mw. It is noted that (1) in many cases, hazard disaggregation is not available to engineers, (2) a site may be characterised by multiple design earthquakes depending on which IM and return period are considered in the analysis, and (3) disaggregation results in terms of PGA may be different from those derived in terms of spectral acceleration or displacement. Nevertheless, in the seismic hazard disaggregation of the numerical example presented in Sect. 4, PGA was preferred over spectral displacement in order to allow comparisons with FBD results. To overcome the three issues stated above, a fully probabilistic design spectrum derived from PSHA in terms of spectral displacements should be used, thus avoiding consideration of a deterministic scenario derived from seismic hazard disaggregation and ensuring consistency with the current state of the art in PBEE. For instance, Smerzini et al. [28] proposed target displacement spectra for Italian sites which were constrained by PSHA results, both at short and long periods. Using that type of displacement design spectra could allow the designer to skip Step 9 of the DDBD procedure presented here, directly applying an alternative formulation in Step 10.
Step 10: Derive Displacement Response Spectra
Based on the design earthquake derived by seismic hazard disaggregation, the elastic response spectrum corresponding to ξel = 5% may be characterised. In this context, Faccioli et al. [29] analysed a large number of digital ground motion records, providing major information on displacement spectra. In particular, those researchers found that: (1) the 5% damped displacement spectra increase rather linearly with period up to a corner period, which is here denoted as TD; and (2) beyond this period, the displacement demand either remains essentially constant (case of strong earthquakes) or tends to decrease (case of moderate earthquakes). Priestley et al. [6] thus stated that, for most structures, it is conservative to consider a constant spectral displacement if T > TD whereas the small non-linearity of displacement spectra at low periods typically has little influence on design. The same researchers also stated that the corner period almost linearly increases with magnitude, suggesting the following equation for a conservative estimation of TD (in seconds):
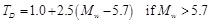 |
(18) |
Besides, the spectral displacement (in millimetres) corresponding to TD may be defined as follows:
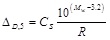 |
(19) |
where CS is a soil-related local amplification factor. Priestley et al. [6] suggested to assume CS equal to 0.7 for rock, 1 for firm ground, 1.4 for intermediate soil, and 1.8 for very soft soil.
More recently, an alternative formulation of the elastic displacement spectrum was made available in literature to ensure a hazard consistent definition of seismic demand on structures [28]. This consists of a specific target displacement spectrum derived from results of long period PSHA for Italy. Although that new approach does not require any assumption in terms of distance and magnitude (opposed to the case of DDBD based on hazard disaggregation, see Step 9), it needs to be calibrated in other countries after that extensive PSHA is carried out by taking into account their different seismicity features. This motivated the use of hazard disaggregation in this study. Nonetheless, the implementation of hazard consistent displacement spectra seems to provide more reliable results in displacement based design, especially in case of long period structures. The use of those spectra will be the scope of a future research where the influence of different formulations for elastic displacement spectrum on displacement-based design of masonry buildings will be numerically investigated.
Regardless of the approach used to define the elastic displacement spectrum, a design spectrum has to be derived in order to account for the inelastic response of the structure. Opposed to FBD where the design acceleration spectrum is defined as constant ductility inelastic spectrum, the design displacement spectrum is here defined as over damped spectrum by considering the following damping correction factor reported in the 1998 edition of EC8‒Part 1 [30]:
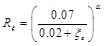 |
(20) |
where the α-factor may be used to account for the source-to-site distance, assuming α = 0.25 if R < 10 km and α = 0.5 if R > 10 km. Given that two equivalent damping ratios ξe,x and ξe,y may be separately defined for the principal directions through Eq. (8) or (10) (depending on whether torsional response is significant or negligible), two damping-related displacement reduction factors Rξ,x and Rξ,y may be estimated.
Step 11: Evaluate the Effective Period and Stiffness of the Equivalent SDOF System
The characterisation of the equivalent SDOF system must be carried out in each direction of the building plan. This characterisation is completed after that the effective periods and stiffness of the structure related to each direction of the building plan are defined. Those parameters may be derived as follows:
 |
(21) |
Step 12: Predict the Design Base Shear and Its Distribution Between Piers
Based on the estimates of effective lateral stiffness and target displacements derived in previous steps, the design base shear in each direction of the building plan may be predicted as follows:
 |
(22) |
Torsional rotation under diagonal excitation is normally neglected in DDBD because on one hand diagonal resistance of the building is typically about 40% greater than that in a principal direction, and on the other hand diagonal displacements of CM are less than those in the principal directions [6]. This is expected to provide large reserve in displacement capacity to allow for torsional rotation. Nonetheless, the effects of bidirectional seismic input on DDBD of URM buildings are assessed in this paper. The base shear in the principal directions may be combined according to different rules, depending on the type of design earthquake. For the sake of simplicity, Priestley et al. [6] defined the type of design earthquake in terms of epicentral distance R, differentiating design earthquakes with R < 10 km from others with R > 10 km. Assuming that horizontal components of the design seismic action are combined as Ed = ± αEx ± βEy, α and β may be set to 0.3 and 1 (or vice versa) if R > 10 km, and α = β = 1 if R < 10 km. In fact, a number of studies have shown that horizontal PGA components of earthquake ground motions at small epicentral distances are very close each other and may even be exceeded by vertical components [31], so combination rules for ordinary design earthquakes may not apply. For instance, the base shear on the i-th pier in the x-th direction may be predicted as follows:
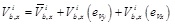 |
(23) |
where:
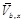 = fraction of base shear associated with translation in the x-th direction, i.e. due to global base shear in the same direction; Vb,x(eVy) = fraction of base shear associated with torsional rotation due to eccentricity in the y-th direction; and Vb,x(eVx) = fraction of base shear associated with torsional rotation due to eccentricity in the x-th direction. Such three strength contributions are defined as follows:
= fraction of base shear associated with translation in the x-th direction, i.e. due to global base shear in the same direction; Vb,x(eVy) = fraction of base shear associated with torsional rotation due to eccentricity in the y-th direction; and Vb,x(eVx) = fraction of base shear associated with torsional rotation due to eccentricity in the x-th direction. Such three strength contributions are defined as follows:
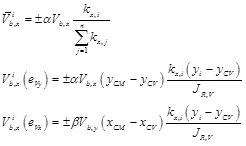 |
(24) |
where a 5% accidental eccentricity is assigned to CM ≡ (xCM,yCM). After that the base shear is distributed between piers, safety verifications in terms of strength may be carried out according to LRFD. If safety verifications are not met, structural geometry and/or strength of walls needs to be modified. The design solution may be optimised in order to minimise construction costs. The displacement based design procedure presented above is summarised by the flowchart in (Fig. 6).
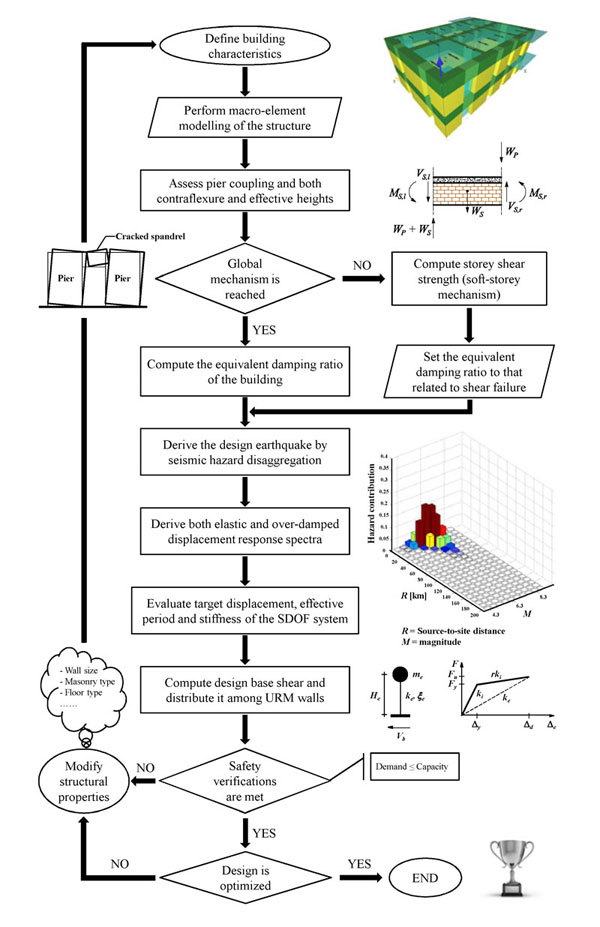
Flowchart of displacement-based design procedure for URM buildings.
4. APPLICATION TO A CASE-STUDY URM BUILDING
A three-storey residential building assumed to be located in L’Aquila, Italy, was designed according to FBD and DDBD procedures. Seismic design was carried out for the limit state of life safety, assuming a design earthquake with return period TR = 475 years or equivalently PVR = 10% in VR = 50 years. The structure was composed of clay brick masonry walls with openings, RC one way floor slabs, and RC slabs for stairs. Fig. (7) show the initial design solution based on architectural choices. The maximum dimensions in plan were 15.70 and 17.90 m in the x- and y-direction, respectively. The inter storey height was set to 3.60 m, resulting in a building height H = 10.80 m. To assess local amplifications of ground motion, a type B ground and type T1 topographic surface were supposed. The nominal properties of brick masonry were as follows: compressive strength fcm = 6.00 MPa; yielding strain εym = 0.25%; Young's modulus E = 6000 MPa; shear modulus G = 2400 MPa; shear strength at zero confining stress fvm = 0.4 MPa; friction coefficient µfm = 0.4; unit weight γm = 15 kN/m3. Regardless of the seismic design procedure, a macro element capacity model of the building was developed. RC bond beams were included in spandrels at the height of floors. Each beam was assumed to have depth equal to 150 mm and width equal to the wall thickness. RC bond beams were assumed to be made of type B450C reinforcing steel with characteristic yielding strength fyk = 450 MPa and type C20/25 concrete with characteristic cube compressive strength fck = 25 MPa.
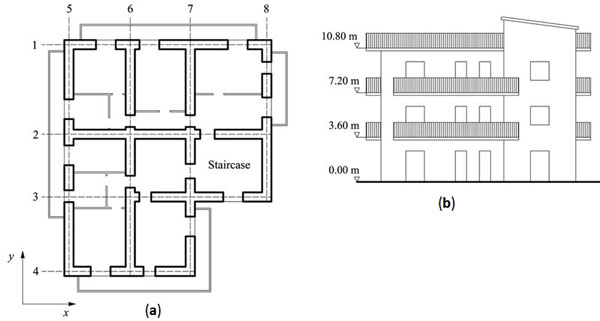
Case-study URM building: (a) plan; (b) lateral view.
The FBD of the building was carried out according to EC8-Part 1 [12] whereas the DDBD solution of the building structure was obtained according to the procedure discussed in Sect. 3. After that a global collapse mechanism was assumed for URM walls, pier coupling was assessed at each floor level by computing the coupling ratio βS. As expected, the piers were found to be uncoupled at the roof level where spandrels behaved elastically. Based on shear forces transmitted by RC bond beams, axial load variations in piers were evaluated and bending failure of piers was expected. Therefore, the assumption of global collapse mechanism was confirmed and the in plane lateral strength of walls was that predicted under the hypothesis of damaged spandrels. Given that the failure mode of piers and the corresponding damping ratio were known, the evaluation of ductility demands on spandrels allowed the estimation of ξe for each wall with openings. The properties of load-bearing walls were then processed to characterise the equivalent SDOF system in each direction of the building plan. The target displacement was evaluated in each direction accounting for torsional response. Seismic hazard disaggregation was carried out through REXEL software [32] which provided a design earthquake with Mw = 6.3 and R = 15 km (Fig. 8a). The corner period and corresponding displacement were evaluated, deriving two design displacement spectra based on Rξ,x, Rξ,y and α = 0.5 (Fig. 8b). Finally, the effective mass, period and stiffness were computed in each direction, allowing the design base shear to be predicted and distributed in plan and elevation.
Table 1 outlines the maximum percentage variations of design base shear for piers from its predictions related to horizontal seismic actions in single directions (that is α = 0 or β = 0) and zero accidental eccentricity ea. Statistics of those variations are also provided in terms of mean and coefficient of variation (CoV). The highest percentage variations were found in case of external walls, indicating that the seismic design of the building was influenced by torsional response. When ea was set different from zero (see columns 2 and 3 in Table 1), the assumptions of design earthquakes associated with R > 10 km and R < 10 km produced different base shear predictions, particularly in the case of perimeter walls in the x-direction (i.e. walls 1 and 4). The distribution of percentage variations is notably scattered between load bearing walls, denoting a mean equal to 8-11% and CoV = 65-74%.
When horizontal seismic actions were combined while considering ea = 0, the magnitude of design base shears on piers was found to be almost equal to that corresponding to single component seismic actions in case of design earthquake associated with R > 10 km (see column 3 in Table 1). On the contrary, in case of design earthquake associated with R < 10 km (column 4), higher percentage variations were detected on perimeter walls in the y-direction (i.e. walls 5 and 8). Finally, when both the seismic load combination and accidental eccentricity were taken into account, percentage variations of up to 18% and 26% were found in case of design earthquakes with R > 10 km and R < 10 km, respectively. The average difference in design base shears with respect to those derived from the classical hypothesis of single component seismic actions was 9% in case of R > 10 km, which increased to 15% in case of R < 10 km. Those base shear variations were rather equally scattered between load bearing walls and CoV was quite high as a result of large variations on perimeter walls and small variations on internal walls. This means that assuming single-component design actions separately in DDBD may cause major underestimation of strength demands on perimeter load bearing walls. This problem becomes even more important if the building is prone to torsional response (as in this case) because of its inherent lack of uniformity in the in plan distribution of strength demands. When a two-component seismic action and non-zero accidental eccentricity were assumed, the distribution of design base shear between load-bearing walls was characterised by a CoV equal to 57% and 61% in case of design earthquakes associated with R > 10 km and R < 10 km, respectively.
Maximum percentage variations of design base shear of piers provided by DDBD.
| Load-bearing wall | ea ≠ 0 | ±αEx ±βEy | ±αEx ±βEy and ea ≠ 0 | |||
|---|---|---|---|---|---|---|
| R > 10 km | R < 10 km | R > 10 km | R < 10 km | R > 10 km | R < 10 km | |
| 1 | 8% | 16% | 1% | 3% | 11% | 21% |
| 2 | 0 | 1% | 0 | 1% | 1% | 1% |
| 3 | 4% | 5% | 0 | 2% | 5% | 8% |
| 4 | 9% | 20% | 1% | 4% | 12% | 26% |
| 5 | 15% | 16% | 4% | 12% | 16% | 24% |
| 6 | 5% | 6% | 1% | 3% | 5% | 7% |
| 7 | 6% | 7% | 1% | 4% | 6% | 9% |
| 8 | 19% | 20% | 4% | 14% | 18% | 26% |
| Mean | 8% | 11% | 2% | 5% | 9% | 15% |
| CoV | 74% | 65% | 107% | 90% | 64% | 66% |
Strength demand to capacity ratios for piers were significantly scattered throughout the building and were notably lower than unity, highlighting the need for structural optimisation. Indeed, DCR was found to be in the range [2%,71%] in case of zero accidental eccentricity and [0.79%] in case of 5% accidental eccentricity. Therefore, linear programming was used to maximise DCR and its uniformity throughout the structure. A two step optimisation process was carried out. The first step was aimed at optimising the wall thickness whereas the second step was aimed at optimising the size of piers and openings. The objective function was assumed to be DCRmin, namely the minimum demand-to-capacity ratio corresponding to the initial DDBD solution for the building. The following bounds were assigned to design variables: wall thickness tw = 0.40-0.80 m; pier length lP ≥ 1.20 m; and opening length lO = 0.90-1.80 m. To ensure convergence, a 5% numerical tolerance on DCR was accepted, resulting in a maximum allowable DCR between 95% and 100%. The same optimisation procedure was applied to the initial FBD solution and a DCR ranging between 21% and 100% was obtained. It is noted that FBD was carried out by considering that the building was irregular in both plan and elevation. That double irregularity produced q = 2.24 according to IBC [13], which provides more accurate estimates for the strength reduction factor to be applied to elastic response spectra.
After that the seismic design optimisation process was completed, the design solutions derived through the FBD and DDBD approaches were compared in terms of construction costs. To that aim, standard parametric costs provided by the Abruzzo Region, Italy, namely the regional administration where the building was supposed to be located, were considered. The total construction cost related to the FBD solution of the building structure was estimated in 279,183 Euros. Conversely, that cost reduced even to 189,482 Euros in the case of the DDBD solution, resulting in about 32% saving. This demonstrates that the DDBD procedure discussed in this study may provide a cost effective design solution for URM buildings, thus responding to the needs of the current PBD philosophy.
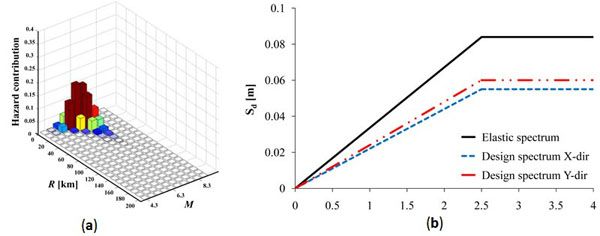
(a) Seismic hazard disaggregation; (b) displacement response spectra.
CONCLUSION
A DDBD procedure for box type URM buildings has been proposed. The effects of the combination of horizontal seismic actions, accidental eccentricity, and type of design earthquake differentiated in terms of epicentral distance, may be taken into account and were assessed in the case of a three storey brick masonry building located in a high seismicity region. The case study building was also designed according to a classical, code based FBD approach. Based on the analysis of the DDBD solutions for the URM building under study, the following conclusions can be drawn: (1) neglecting the combination of horizontal seismic actions and accidental eccentricities within DDBD may result in dangerous underestimation and wrong distribution of strength demands between load bearing walls; and (2) the seismic response of the URM building also depends on whether the design earthquake is assumed to be associated with small or large epicentral distances. The latter assumption affects both the design spectrum and load combination rule to be used in the DDBD approach.
Finally, seismic design was optimised so that safety factors were minimised and construction costs resulting from FBD and DDBD design solutions were estimated for the case study building. It has been found that DDBD may provide construction costs significantly lower than those resulting from code based FBD procedures.
CONFLICT OF INTEREST
Declared none.
ACKNOWLEDGEMENTS
This research was carried out in the framework of ReLUIS-DPC 2014 project (Line 1 - Masonry Structures) under funding of the Italian Civil Protection Department. Ideas for this study were born from discussions with Prof. Nicola Augenti who is gratefully acknowledged.


