All published articles of this journal are available on ScienceDirect.
Analysis on Dynamic Response of Reinforced Concrete Frame for Resisting Progressive Collapse
Abstract
In order to investigate the dynamic response of reinforced concrete spatial frames caused by initial damages, a six-story frame model is analyzed by employing the nonlinear dynamic methodology in accordance with the alternate path method issued by General Services Administration. In this paper, the fiber model and force-based beam-column element are utilized in OpenSees. Four various scenarios are separately analyzed with incremental dynamic analysis. It is shown that the model does not collapse and the internal force redistribution mainly appears in the components adjacent to the failure column. The model has the worst capacity to resist progressive collapse in the inner column demolition scenario. It is observed that the plastic hinges mainly concentrate on the beam ends of the failure bay at the beginning of the demolition of columns. Several plastic hinges emerge at the top-floor beam ends of some other bays in latter period. The number of plastic hinges in columns is much less than that in beams, which corresponds to the design principle ‘strong column and weak beam’.
1. INTRODUCTION
From the Ronan Point apartment building collapsed in England in 1968 to the terrorist attacks on World Trade Center towers in 2001, progressive collapse has caused huge casualties and property losses. Generally, progressive collapse is defined as the spread of an initial local failure from element to element eventually resulting in the collapse of an entire structure or a disproportionately large part of it [1]. To prevent progressive collapse, a structure should have sufficient redundancy to offer an alternate load path to sustain the redistributed loads. Design guidelines [2, 3] have proposed design procedures to assess progressive collapse potential of the structure subjected to the loss of columns.
In recent years, many studies have been carried out in terms of progressive collapse issue. Marjanishvili and Agnew [4] used four basic approaches to analyze a steel moment-resistant frame building and concluded advantages and disadvantages of these approaches. Kim and Yu [5] revealed that the catenary action could increase the capacity to resist progressive collapse and structures designed considering seismic loads showed superior performances against progressive collapse. Tsai and Lin [6] proposed that a constant dynamic amplification factor equal to 2.0 was conservative for estimating the collapse resistance of a ductile column-removed building and the capacity curve could be applied to prediction of the collapse resistance. Kokot et al. [7] investigated a real-scale reinforced concrete flat-slab frame building and made numerical study considering three loading scenarios. Iribarren et al. [8] used a more sophisticated approach consisted of a detailed modeling of reinforced concrete cross-sections to analyze a five-story RC planar frame model. Yi et al. [9] conducted a static experiment of a four-bay, three-story and one-third scale RC planar frame, simulating the load transmission process. The experimental results showed that the frame with middle column failed would go through three phases including elastic, plastic and catenary phases. Qian and Li [10] conducted seven one-third scale RC beam-column substructures to investigate the behavior under the scenario of being subjected to the loss of one ground corner column. It was proposed that increasing the flexural capacity of the beam section and upgrading the shear strength of the corner joint could improve the performance of frames against progressive collapse. De Biagi and Chiaia [11] proposed an analysis based on graph theory referring to frames. A beam importance factor was then deduced and preliminary robustness properties were discussed. Three examples were proposed in order to examine the capabilities of the complexity indices and the beam importance factor. Tavakoli and Kiakojouri [12] investigated the progressive collapse capacity of steel moment-resisting frames, made suggestions for assessment of structural robustness and quantified the robustness of frames. The results clarified that the robustness and progressive collapse potential of the frames varied significantly, depending on the location of the initial local failure and number of building stories. Palmisano [13] found that the activation of the elasto-plastic catenary behavior of the slab reinforcement could be very effective to increase the building robustness without substantially increasing the cost of a structural system.
The research on the issue of progressive collapse has just started in China. Many existing buildings have not been designed to resist progressive collapse. Meanwhile, most of the relative investigations are carried out on 2D frames without considering the spatial effect of frames. Thus, it is necessary to evaluate the collapse-resistance performance of the existing structures designed in accordance with the requirements of Chinese code by establishing 3D finite element models. In this paper, using the alternative path method, the response of a six-story reinforced concrete structure following loss of load-bearing elements is studied to assess the possibility of collapse. The IDA method conventionally adopted in the seismic analysis is performed herein to obtain the collapse-resistance capacity to determine the most vulnerable component conveniently. Based on the development of plastic hinges of the frame, the collapse process could be more comprehensive and intuitive.
2. ELEMENT AND MATERIAL
2.1. Element Type
There are three kinds of nonlinear beam-column elements in OpenSees: displacement-based beam-column element, force-based beam-column element and beam with hinges element. In this paper, the frame beam and column elements are simulated using the force-based beam-column element. By determining the resistance and stiffness matrix of control sections, the resistance and tangent stiffness matrix of the entire element is integrated along the length in the light of Gauss integration.
2.2. Material Properties and Constitutive Models
The element is composed of the fiber sections in which material properties of concrete and steel bars are respectively assigned to the fibers. As displayed in Fig. (1), Hysteretic Material from OpenSees is employed herein to model steel bars. Concrete02 Material derived from the modified Kent-Park model [14] is used to describe the stress-strain relationship of concrete, shown in Fig. (2). The section of beams or columns is divided into the protective layer concrete and core concrete with stirrup constraints in modeling. The ultimate compressive strain of the protective layer concrete is taken as 0.004, while the ultimate compressive strength is taken as 0 MPa in consideration of the spalling of concrete. The concrete strength enhancement coefficient K needs to be taken into account in the core concrete. Its constitutive equations of the model and related parameters are defined as follows:
when εc ≤ 0.002K,
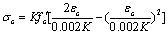 |
(1) |
when εc > 0.002K,
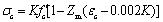 |
(2) |
when εc > εu,
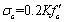 |
(3) |
where K and Zm are, respectively, the concrete strength enhancement coefficient due to stirrup constraints and the strain softening slope. They are mathematically expressed as:
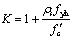 |
(4) |
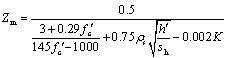 |
(5) |
where
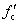 and
and
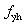 are the concrete cylinder compressive strength and the stirrup yield strength, respectively. ρs stands for the volume-stirrup ratio of beams or columns. h' and Sh are, respectively, the width of the core concrete and the stirrup spacing. The ultimate compressive strain of the core concrete is derived as:
are the concrete cylinder compressive strength and the stirrup yield strength, respectively. ρs stands for the volume-stirrup ratio of beams or columns. h' and Sh are, respectively, the width of the core concrete and the stirrup spacing. The ultimate compressive strain of the core concrete is derived as:
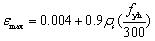 |
(6) |
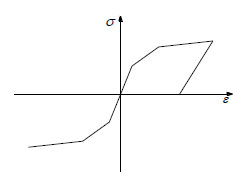
Rebar constitutive model.
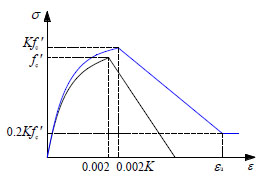
Concrete constitutive model.
2.3. Model Validation
In order to validate the accuracy of the finite element analysis in this paper, the experimental test performed by Yi et al. [9] on a planar frame was numerically simulated with the OpenSees software. Fig. (3) shows the comparisons between calculated and experimental results. It can be seen that good agreement is achieved in initial stage, and there is a slight gap in latter period due to the fracture of steel bars in beams. In general, the finite element model is accurate enough to conduct the progressive collapse analysis, which can provide advices for further analyses in other scenarios.
3. RC FRAME DESIGN AND MODELING
3.1. Building Characteristics
A six-story RC frame structure is designed in accordance with the concrete design code of China [15]. The layout of the frame is displayed in Fig. (4). Fig. (5) depicts the dimensions of column and beam sections in details with slab thickness of 100 mm. The concrete strength grade of beams, floors and columns is C30, which is estimated at approximately 24 MPa for a standard concrete cylinder. The concrete protective layer thicknesses of beams, floors and columns are 25 mm, 15 mm and 30 mm, respectively. The yield strength is 335 MPa for the main reinforcements and 300 MPa for the stirrups. The structure is designed for 7 degree. The corresponding PGA (peak ground acceleration) value of the design earthquake (i.e., a 10% probability of exceedance over a 50-year interval) is 100 cm/s2. The dead loads are 6 kN/m2 for roof and 4 kN/m2 for other floors. The live loads are 0.5 kN/m2 for roof and 2 kN/m2 for other floors. Also a partition wall weight of 9 kN/m is considered at every floor, except in roof level. The ground roughness is C class and the basic wind pressure w0 is 0.5 kN/m2. The reinforcements of beams and columns at each floor derived from PKPM software are shown in Fig. (5).
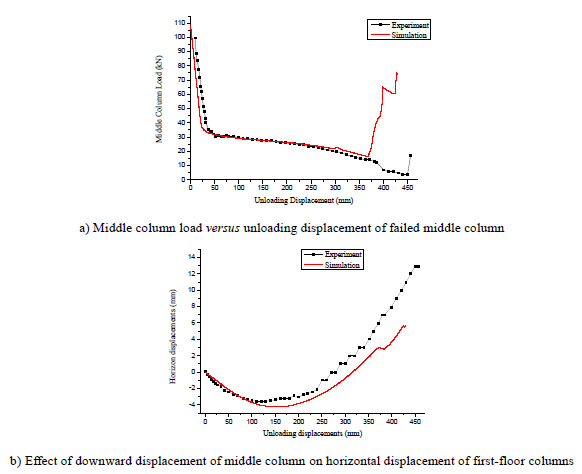
Comparison of experimental and simulated results.
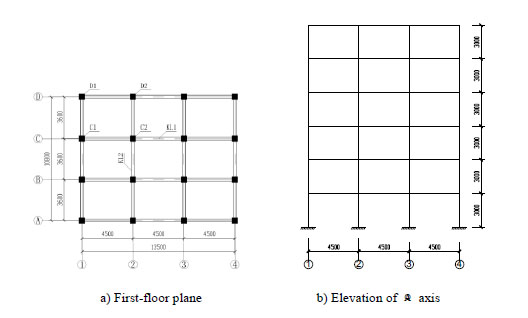
Model layout (units: mm).
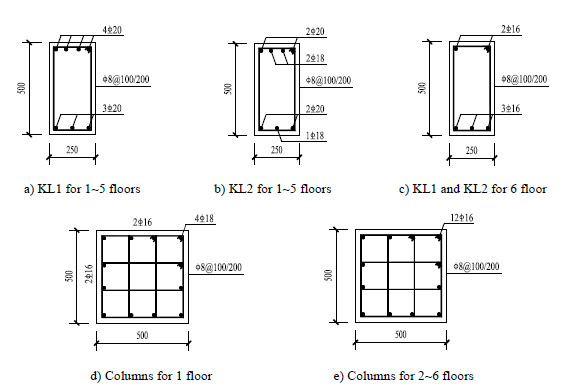
Reinforcement details of beams and columns (units: mm).
It should be noted that slabs are not considered in the modeling on which loads are applied to the adjoining beams by the rule of the two-way slab instead. GSA provides application of a nonlinear dynamic analysis, in which the following load combination is employed:
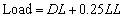 |
(7) |
where DL and LL are dead load and live load, respectively [3].
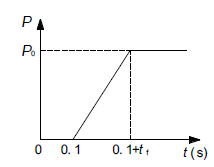
Loading function.
3.2. Analysis Method
The alternative path method provided by GSA guideline is used with the consideration of the gravity second order effect and the nonlinearity of the structure. The steps required in performing the analysis are: 1) build the finite element model which is shown in Fig. (4); 2) perform nonlinear static analysis to estimate the internal force P0 at the top of the removed column; 3) perform modal analysis on the residual structure; 4) impose the internal force P0 on the residual structure in the opposite direction to make the analysis model static equivalent to the primary model, apply the downward load shown in Fig. (6) at the top of the removed column and perform nonlinear dynamic analysis. In Fig. (6), tf is the failure time which is as 0.1 times as the fundamental period of the residual structure [3].
3.3. Analysis Parameters
In this paper, four principal scenarios have been considered: sudden removal of the short-side middle column C1, the inner column C2, the corner column D1 and finally the long-side middle column D2 on the first floor, one at a time. They are designated as Case C1, Case C2, Case D1 and Case D2, respectively. The fundamental period T00 and the first two frequencies ω1 and ω2 of the residual structure derived from modal analysis can be employed to calculate the mass damping coefficient α and the stiffness damping coefficient β of Rayleigh damping. The damping ratio of concrete is 0.05 and related parameters are shown in Table 1 in which t denotes the total time of each time-history analysis.
Analysis parameters.
| Case | t (s) | T00 (s) | tf (s) | ω1 (rad/s) | ω2 (rad/s) | α | β |
|---|---|---|---|---|---|---|---|
| C1 | 10 | 0.492 | 0.049 | 12.783 | 13.454 | 0.655 | 0.003811 |
| C2 | 10 | 0.488 | 0.049 | 12.865 | 13.446 | 0.657 | 0.003801 |
| D1 | 10 | 0.499 | 0.050 | 12.597 | 13.253 | 0.646 | 0.003868 |
| D2 | 10 | 0.488 | 0.049 | 12.865 | 13.230 | 0.652 | 0.003832 |
As the two-way shear and torsion are not coupled in the fiber section of OpenSees, the shear stiffness and torsional stiffness need to be defined as a supplement. The shear stiffness and torsional stiffness of beam and column sections are displayed in Table 2, in which Asy and Asz are the shear area along y-axis and z-axis direction, T is the torsion constant, Ec and Gc are the elastic and shear modulus of concrete, ksy and ksz which are evaluated according to Eqs. (8) and (9) are the shear stiffness along y-axis and z-axis direction, and kt derived from Eq. (10) is the torsional stiffness.
Shear and torsional stiffness of sections.
| Section | Asy (mm2) | Asz (mm2) | T (109mm4) | Ec (MPa) | Gc (MPa) | ksy (109N) | ksz (109N) | kt (1014N·mm2) |
|---|---|---|---|---|---|---|---|---|
| Column | 208333.33 | 208333.33 | 8.80 | 29791.46 | 12413.11 | 2.59 | 2.59 | 1.09 |
| KL1 | 104166.67 | 104166.67 | 1.79 | 29791.46 | 12413.11 | 1.29 | 1.29 | 0.22 |
| KL2 | 104166.67 | 104166.67 | 1.79 | 29791.46 | 12413.11 | 1.29 | 1.29 | 0.22 |
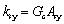 |
(8) |
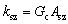 |
(9) |
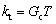 |
(10) |
4. NONLINEAR DYNAMIC ANALYSIS
4.1. Displacement-Time Curve
The vertical displacement-time curves of the joint (top of the failed column) in the four scenarios are displayed in Fig. (7). Vertical displacements firstly increase monotonically, then fluctuate and finally decay to a stable state. Prescribed values provided by GSA aren’t exceeded by rotations at beam ends of the residual model, which implies the residual model will reach a new equilibrium state and progressive collapse will not happen. The maximum vertical displacements in Case C1, C2, D1 and D2 reach 4.29 mm, 5.61 mm, 5.81 mm and 6.04 mm at 0.17 s, 0.17 s, 0.18 s and 0.17 s, respectively. Because of suffering from the less restriction, the curve fluctuation in Case D1 takes longest and reaches the greatest value in magnitude. The fluctuation ranges and durations in Case D2 and C1 decrease in sequence. It can be seen that the curve fluctuation in Case C2 firstly stops to a stable state due to the strongest beam constraints.
4.2. Internal Force of First-Floor Columns
Internal forces of beams and columns vary to different extents due to the redistribution of loads after the removal of supporting members. In this paper, the axial force-time curves at the bottom section of first-floor columns in Case C1 are displayed in Fig. (8). It is seen that the axial forces of columns in A axis which are far from the failure column are small and change little. The removal of Column C1 which is a side column creates an anti-clockwise moment of the entire structure to pull the right side columns and press the left side columns. The axial forces of Columns A1 and A2 fluctuate in a direction opposite to those of Columns A3 and A4. The fluctuation range of side columns A1 and A4 are obviously greater than those of middle columns A2 and A3. It is noted that the axial force of Column B1 which is adjacent to the failure column increases 47.6% to 1053.7 kN and fluctuates in the opposite direction to Column B4. The axial force of Column B2 increases a little at first and the axial forces of Columns B3 and B4 change little. Similar to columns in A axis, the axial force fluctuation ranges of side columns in B axis are greater than those of middle columns. The axial force of Column C2 instantaneously increases 16.5% to 1233.6 kN and its fluctuation range is smaller than Column C4 in latter period. Though Column C4 is in the same frame with the failure column, its redistributed axial force is very small and the changing process is similar to Column B4. It should be noted that the axial force of Column D1 increases 64.7% to 838.6 kN. The axial force of Column D2 increases a little and the axial forces of Columns D3 and D4 almost remain unchanged.
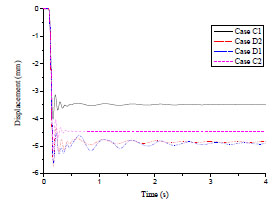
Vertical displacement-time curves of joints.
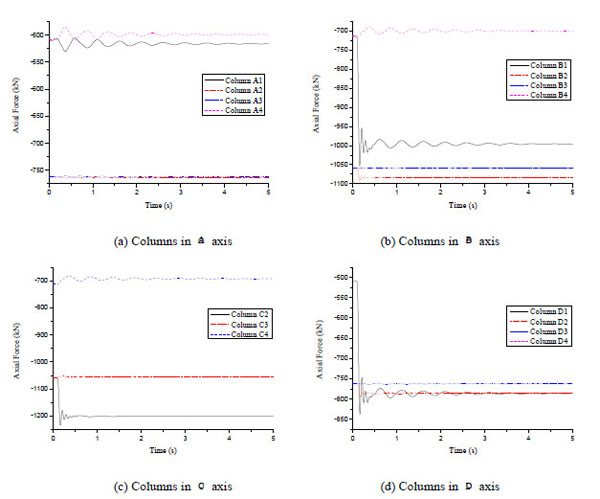
Axial force-time curves of first-floor columns in Case C1.
In combination with other scenarios, it can be concluded that axial forces of columns adjacent to the failure column initially increase rapidly and then reach a stable state. Axial forces of columns far from the failure column have small initial amplitudes and change little. It is indicated that internal force redistribution caused by the demolition of the supporting member concentrates on the members adjacent to the failure column. In the side and corner column demolition scenarios, axial forces of side columns fluctuate with large amplitudes and a long time owing to the entire moment. In the inner column demolition scenario, force redistribution complete with small amplitudes in a shorter time compared with side and corner column demolition scenarios.
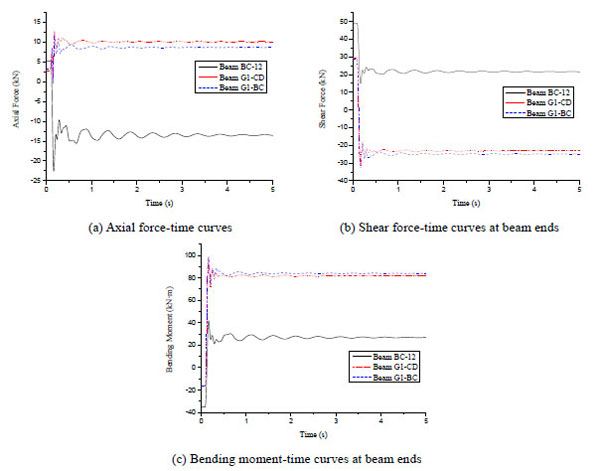
Internal force-time curves of beams close to the failure column in Case C1.
4.3. Internal Force of First-Floor Beams
Internal forces of beams connected to the failure column change a lot subsequent to the demolition of the failure column. Internal force-time curves of beams in Case C1 are shown in Fig. (9). In the serial number of beams, initial B or G implies that beams are along the long or short span direction respectively. The second letter stands for the axis in which the beam lies. The last two letters indicate the beam location. In this paper, it is prescribed that the axial tension is positive and the axial pressure is negative; the upward shear force is positive and the downward shear force is negative; the bending moment is positive when the lower section is drawn and the upper section is under pressure.The axial forces of Beams G1-CD and G1-BC remain tensions and increase a little. The axial force of Beam BC-12 changes to compression from tension. It can be seen that the shear forces at beam ends all reduce, in which Beams G1-CD and G1-BC have bigger decline. The bending moments at beam ends change directions and the moments of Beams G1-CD and G1-BC increase remarkably.
In combination with other scenarios, it is indicated that axial forces of cantilever beams which once are tensions significantly reduce to be pressured. Whereas the axial forces of middle beams still are tensions and increase a little. All the shear forces at beam ends close to the failure column decrease after the demolition of the failure column. Compared with beams along long span direction, shear forces of beams along short span direction reduce more dramatically. All the bending moments at beam ends close to the failure column change directions. It is seen that bending moments of beams along short span direction increase more remarkably.
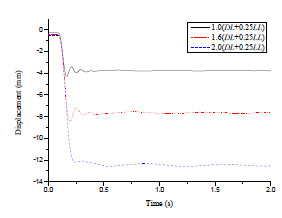
Vertical displacement-time curves in Case C1.
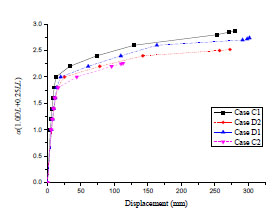
IDA curves.
5. COLLAPSE RESISTANCE ANALYSIS
A series of nonlinear dynamic analyses are conducted to obtain structural collapse resistance by increment dynamic analysis (IDA) [16]. The load α (DL+0.25LL) is applied at each level in which α is increased by 0.2 from 1. When the analysis approaches the point of divergence, α is increased by 0.01 until the ultimate state of collapse. In Fig. (10), the vertical displacement-time curves subjected to different loads in Case C1 are displayed. Fig. (11) depicts the related IDA curves in the four scenarios. The collapse resistances reach 2.87, 2.26, 2.74 and 2.52 times of (DL + 0.25LL) at vertical displacement of 280.57, 112.86, 301.64 and 272.64 mm for Case C1, C2, D1 and D2, respectively. In light of this, both collapse resistance and deformability for Case C2 are the worst of all. As the frame could sustain the vertical loads far beyond its design loads, it could be concluded that the seismic design of structures could enhance the progressive collapse potential to some extent.
To study the failure mechanism of structural collapse, the model in the ultimate state of collapse is analyzed in which plastic hinges are fully developed. In the collapse-resistant analysis, the flexure failure is the main failure mode in the beams, in which the plastic hinges at the beam ends are defined to easily describe the flexure status of beams when the tensile reinforcements are converted into yielding state. The sequences and distributions of plastic hinges under various cases could illustrate the complete collapse process of the frame as shown in Fig. (12). In the serial number of beams, the figure in brackets stands for the floor which the beam is on. The letter L or R implies the left or right end of the beam. For the short-span beams, it is stipulated that from D to A axis is from the left to the right. For the long-span beams, it is stipulated that from 1 to 4 axis is from the left to the right. In the serial number of columns, initial C implies columns; the second and third letters stand for the axes in which the column lies; and the letter B or U implies the bottom or upper end of the column.
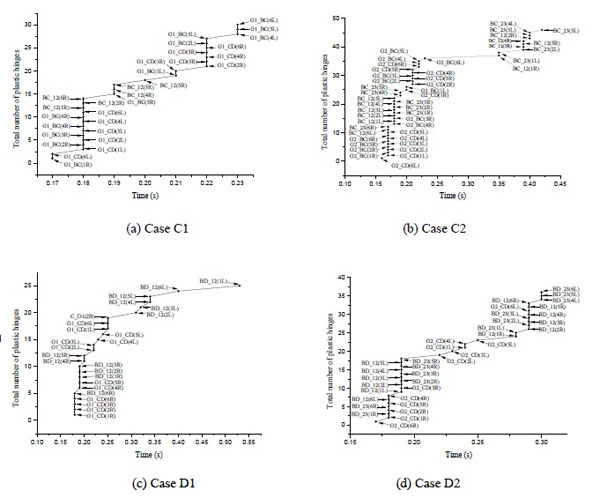
Sequences of plastic hinges.
It is observed that the plastic hinges mainly concentrate on beam ends of the failure bay at each story. Plastic hinges of columns develop slowly and only emerge at the bottom of Column D1 on the second floor. The upper reinforcement at beam ends which is far from the failure column yields earlier than the lower reinforcement at beam ends adjacent to the failure column. In the four scenarios, plastic hinges of beams along the short span direction develop faster than those of beams along the long span direction. Table 3 summarizes plastic hinges conditions in latter period. As several plastic hinges emerge at top-floor beam ends in some other bays and the corner column close to the failure column, it is need to take steps to strengthen these weak components to prevent collapse. It is demonstrated that the development of plastic hinges basically corresponds to the design principle ‘strong column and weak beam’.
Occurrence time of plastic hinges in later period.
| Case | C1 | C2 | D2 | ||||
|---|---|---|---|---|---|---|---|
| Location | C_D1(2B) | G1_CD(6L) | G1_CD(6R) | G1_BC(6L) | G1_BC(6R) | BD_12(6L) | C_D1(2B) |
| Time/s | 2.2 | 2.45 | 1.81 | 2.26 | 4.74 | 1.83 | 3.93 |
CONCLUSION
In this paper, a finite element model designed in accordance with the requirements of Chinese code is developed to evaluate dynamic response of RC frames subjected to column loss in details. Based on the findings from the analysis described in this paper, the following conclusions can be drawn:
1. It is indicated from the nonlinear dynamic analysis that the model designed in accordance with the concrete design code of China does not collapse in different scenarios. As the redistribution of internal force caused by the demolition of the ground column is mainly concentrated in the adjoining components with little influence on other members, the enhancement of the critical members in possible failure area could prevent progressive collapse effectively;
2. Through the vertical incremental dynamic analysis, the collapse-resistance capacities of the four scenarios are conveniently evaluated to determine the most vulnerable component. It should be noted that the frame model has the worst collapse resistance and deformability in the inner column demolition scenario. Thus, the inner column is comparatively weak load-bearing member which needs to be strengthened; and
3. It is observed that the plastic hinges are mainly concentrated on beam ends of the failure bay, which indicates that the beams connected to the failure joint transfer the loads sustained by the initial damaged column to the adjacent components. The number of plastic hinges in columns is much less than that in beams corresponding to the design principle ‘strong column and weak beam’, which implies that the frames designed according to the existing criterions have certain ability to resist progressive collapse.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The work presented in this paper was funded by the National Natural Science Foundation of China (No. 51178304), the Special Research Foundation of Doctor Station in Chinese University (No. 20120032120055) and Application Base and Advanced Technology Research (Youth Foundation) (N0. 12JCQNJC05000), which are gratefully acknowledged.


