All published articles of this journal are available on ScienceDirect.
Numerical Investigation of Innovative Support Frame of Openings in the Segmental Tunnel Lining
Abstract
Introduction:
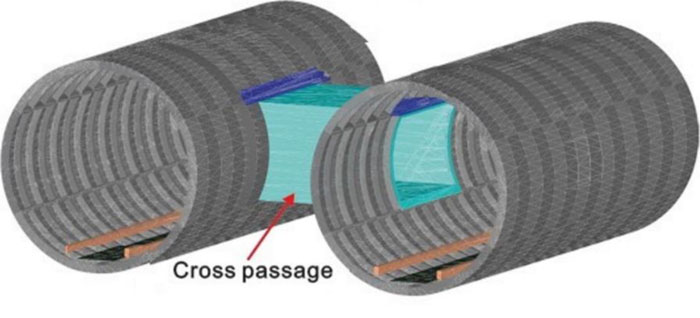
To supply safety in the tunnels, it is necessary to construct escape routes and emergency exits that are performed by locating cross passages.
Methods:
These passages connect two tunnels transversely and apply escape routes. Using temporary steel structures to supply the ring stability in practice and reinforced concrete frame to stabilize the ring permanently can be appropriate to form a solid frame that transfers the opened ring's load to the opening surroundings. In this paper, a 3D finite element simulation was performed to analyze the influence of opening construction in the segmental concrete lining and a temporary support system. Using the simulation, stress and deformation distribution of the steel frame, bolts, and segmental lining were obtained.
Results:
The results show that by increasing the number of bolts from 18 to 30, the induced stress in the steel frame and bolts decreased to 76 and 59 percent, respectively. In addition, the maximum displacement in the segmental lining and the maximum opening value of the joints decline to 62.7 and 75 percent, respectively.
Conclusion:
Finally, it can be concluded that the steel frame can be used as a temporary support system.
1. INTRODUCTION
Designing and construction of tunnels are one of the most critical and essential challenges in mining and civil engineering from past to present. Nowadays, mechanized tunneling is developed all around the world [1-5]. To investigate the conditions of a tunnel, an analytical solution derived from 2D plane-strain models is extensively adopted [6, 7]. Such conventional 2D methods allow engineers to investigate the general behavior of a full tunnel ring, but they are unable to investigate the performance of some special structural features such as cross-passage openings [8].
The development of transportation in metropolitans and the underground geotechnical conditions make the construction of twin tunnels essential. Moreover, twin tunnels have many advantages than the single tunnel with large sizes, such as reducing tunnel diameter and soil displacement caused by tunneling, the possibility of investment in a different phase, more stability, and better ventilation. Constructing the escape routes and emergency exits play a vital role in tunnels safety, which are performed by locating cross passages with specified intervals throughout the tunnels. These passages connect two tunnels transversely and apply escape routes inside the other tunnels and shafts (Fig. 1).
These massive concrete structures consist of a formed structural frame using rebar and molded concrete in particular conditions. The segments are joined together like puzzle pieces and form a segmental ring. This ring is attached to adjacent rings and forms a uniform system. The joints between segments cause the reduction in lining rigidity. Several methods have been developed to analyze the segmental lining behavior. The simulation progress of the longitudinal and circumferential joints in the segmental lining would improve these approaches. In recent years, many researchers simulated segmental joints to investigate their influence on structures’ behavior by analytical and numerical methods. Blom (2002) considered the segment joints in the tunnel lining by analytical methods. Considering the impact of the soil-structure interaction and adjacent segmental rings was the novelty of Blom's analytical solution. Koyama (2003) introduced diagrams of the bending moments in relation to the rotational angle joints. In their paper, the values of the rotational stiffness of springs (KRO) are in the range from 15 to 150 MN.m/rad. Hefny et al. (2004) modeled tunnel segmental lining using the finite element method. Various parameters, including the number of segments, joint position, lateral earth pressure coefficient, depth to tunnel diameter ratio and tunnel flexibility ratio, were investigated. It was observed that the number of segments and joint pattern has a major effect on the maximum bending moment induced in the segmental lining [9-19]. The mentioned studies have been performed on the segmental tunnel joints; the cross-passage openings generally have been poorly studied. The influence of joints on segment behavior can be considered directly and indirectly [20]. From the structural point of view, the segmental ring can be modeled as a ring with several joints or a continuous lining with a reduction factor. In an indirect approach, the lining is considered as a continuous ring in a continuous environment. The effect of joints is taken into account by applying a reduction coefficient of rigidity, and the ground-structure interaction is considered with specific springs based on Winkler theory. In the direct approach, the joints are added to the liner directly [21]. In numerical modeling, all three stiffness could be investigated, which in most of them, the joint behavior is modeled using rotational spring [22].
To excavation a cross-passage, appropriate practical approaches must be utilized, which should contain the improvement of lining in the opening range and compensate for the segmental ring's structural weakness. To supply the required load-bearing capacity around the opening in the segmented tunnels, steel frames, steel segments, and particular concrete segments can be used [23, 24]. By removing segments from desired rings, the ring is opened and loses its closed structural behavior. Therefore, it is necessary to tolerate the circular forces using other structural elements temporarily during the construction and permanently after the construction and during the operation. In order to provide the required load-bearing capacity around the opening in the segmental tunnel lining, using steel segments is relatively costly due to the existence of permanent segments and time-consuming performance. Furthermore, some arrangements should be considered (on the interior) against fire and corrosion. In addition, using special concrete segments compared to the ordinary reinforced concrete has a higher production cost and reinforcement level. Another disadvantage of this approach is the installation accuracy of the segments, which should be bolted together. During the bolt connections design, to determine the structural manner of such connections, the cracking path and their load transmission capacity, experiments, and numerical analysis are suggested.
If the galleries layout is finalized before the tunnel construction ended and special arrangements could be made, it is possible to use the mentioned approaches. However, for the projects where the galleries are constructed after the tunnel construction, and there are no specific arrangements in location, a practical method with technical consideration must be presented. Utilizing a temporary steel frame is suis for ring stability during the practice and reinforced concrete frame for permanent ring stability to form a solid frame that transfers the opened ring's load to the opening surrounding. This research, in addition to the modeling results, is useful for designing and optimizing the performance of the opening in a condition that particular segments are not possible, or temporary steel frames are used to reduce costs.
In this study, a three-dimensional finite element analysis was performed to investigate tunnel lining and structural components' mechanical behavior [25]. To maintain the tunnel lining stability after the construction of the opening, a temporary support system is considered. This study's results can be used for the efficient design of openings, costs reduction, and speeding up the construction process. The study on segmental tunnels cross-passage in the form of Structural can be an innovation of this research. Finally, the influence of the opening on the steel frame, bolts, and segments behavior is investigated. Moreover, the opening rate of the longitudinal joints of rings containing the opening is analyzed.
2. NUMERICAL MODELING
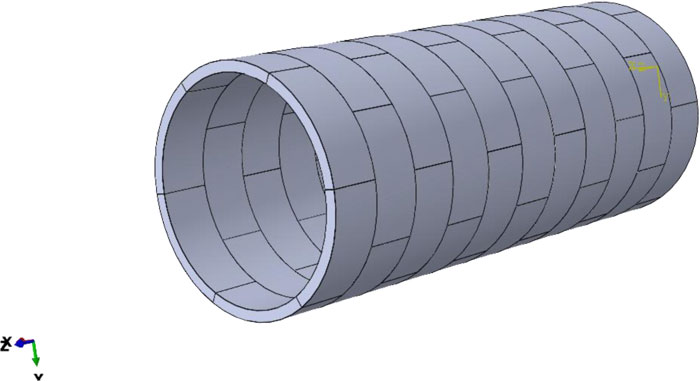
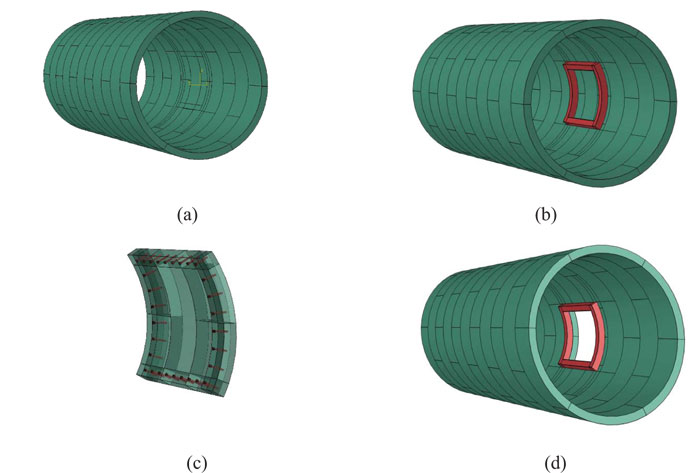
To modeling the tunnel lining, concrete segments are used. Each segmental ring consists of six segments, and the external diameter is 6 m. Fig. (2) shows the arrangement of the concrete segmental lining. The segments have a staggered arrangement, and therefore, the longitudinal joints of each ring were matched with the center of segments in the next ring. This configuration increases the lining's stability and decreases the possibility of leakage in the tunnel lining. Table 1 shows the geometrical and physical properties of the concrete segments.
At the first step of the simulation, the tunnel was stabilized and balanced by its weight and geostatic load. In the next step and before the opening construction, a temporary support system was installed inside the tunnel lining with 18 bolts, as shown in Fig. (3). Subsequently, the excavation process was started, and the effect of the structural components was investigated. To simulate the defined two phases, the stage construction method was employed in the modeling. The hexagonal elements shape was used, and the meshing technic was sweeping. The size of the elements around the opening and frame holes were considered smaller than the other areas.
Using solid elements for the tunnel lining permits to consider the real thickness of the segmental joints [26].
| thickness (cm) |
Width (cm) |
Density (kg/m3) |
Poisson Ratio | Elasticity Module (MPa) |
Rupture Module (MPa) |
Uniaxial Compressive Strength (MPa) |
| 30 | 130 | 2500 | 0.2 | 32000 | 4.69 | 45 |

Segments were then created using solid elements, whereas contact elements were used to model the contact and the friction coefficient of the segmental joints. The friction coefficient of the longitudinal joints and the transversal joints was considered as 0.7 and 0.3, respectively.
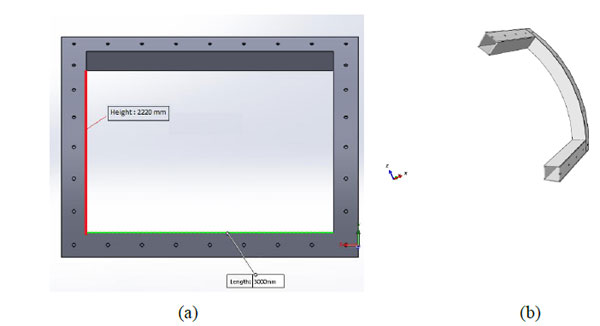
The used temporary support system consisted of a steel frame and the linking bolts. The steel frame was coupled to the segmental lining by steel bolts. The material of the frame and bolts is ST37 steel. In order to prevent the steel frame from bending and torsion against the applied loads, the frame was designed with a shell shape (Fig. 4a). This technic increases the torsion moment and bending moment of inertia, which causes to improve the bending/torsional strength of the frame. The inner height of the frame and the width of the frame are 2.22 m and 3 m, respectively (Fig. 4b), while the thickness of the frame shell is about 20 mm.
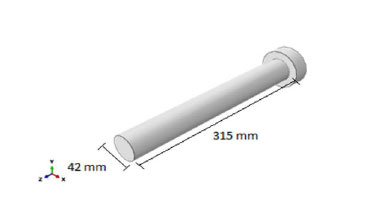
As mentioned before, the steel frame is joined to a segmental lining with steel bolts. The length of the bolts is 315 mm (see Fig. 5). Like the steel frame, bolts are made of ST37 steel with an elasticity modulus of 210 GPa and the Poisson ratio of 0.3.
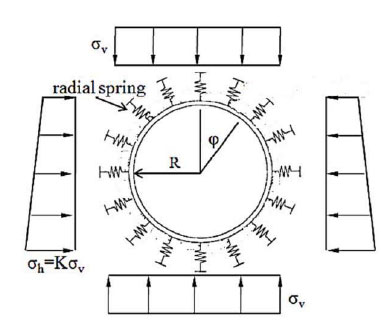
To simulate the interaction between soil and tunnel, springs with nonlinear stiffness were used. These springs only resist the pressure load and they have no resistance against the tensile load. Fig. (6) shows springs for defining the interaction between the soil and the tunnel.
To considering the theory of elasticity, and the interaction of the ground surrounding the tunnel, the reaction coefficient of the ground is calculated by using Eqs. (1) and (2), as follow [27]: where Kr is radial spring stiffness, Kt is tangential spring stiffness, E is the elasticity modulus of soil, v is the Poisson ratio of soil, Req is the equivalent radius of the tunnel.
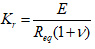 |
(1) |
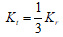 |
(2) |

The connection between the bolts, frame and segments also follows the same approach. Bolts were fixed into the segment holes to prevent additional movements. The cross-passage opening excavation was performed in two steps. First, the tunnel was stabilized and balanced by its weight and the geostatic load. Then, the steel frame was installed in the determined location, and the tunnel lining was removed. Therefore, the additional load resulted from the opening construction was transferred to the steel structure.
Different analytical and numerical methods can be used to calculate the effective vertical load on the tunnel. In this regard, Terzaghi's analytical method was chosen for obtaining the ground load on the tunnel (Eqs. 3-5) [28]. The schematic view of the loading is shown in Fig. (7). Values of the parameters are tabulated in the Table 2. In addition, the excavation procedure of opening consists of three steps, shown in Fig. (8).
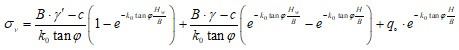 |
(3) |
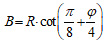 |
(4) |
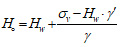 |
(5) |
| Parameter |
q0 (kpa) |
B (m) |
R (m) |
H (m) |
Yt (kn/m3) |
K0 |
ϕ (deg) |
c (kpa) |
| Value | 0 | 5.44 | 3.3 | 10 | 15 | 0.428 | 35 | 20 |
Where H and B are depth of excavation from the tunnel crown and span of the tunnel, respectively, H0 is height of Terzaghi's rock load, k0 is coefficient of the lateral earth pressure in the static state, c is cohesion of the rock, φ is angle of internal friction, Hw is water table, γ is unit weight of the ground, γ' is unit weight of saturation, q0 is surface load of the ground, σv is vertical stress of the ground, R is radius of the tunnel.
3. RESULTS AND DISCUSSION
The numerical analysis is conducted in two scenarios. In the first state, the frame is connected to the tunnel lining through 18 bolts. However, for investigating the effect of bolts number on supporting system behavior, the number of the bolts was increased to 30 in the second mode. Finally, the results in both scenarios were compared with each other.
In each mode, two parts were considered. In the first section, the results were presented before the opening excavation. In this phase, the supporting system was not installed, and the tunnel was stabilized with soil load and weight. In the second part, the frame was installed, and the opening was constructed in the tunnel lining. Fig. (9) shows the Mises stress distribution before opening construction in the segmental lining (the values are according to MPa in all figures).
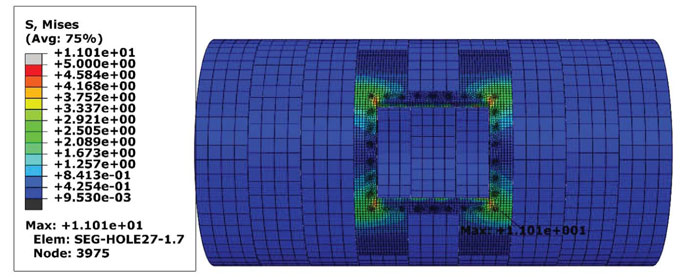
Based on Fig. (9), there is no stress concentration, and the tunnel lining is in the equilibrium state corresponding to the external loads. Fig. (10) illustrates the induced stresses in the segmental lining after opening construction based on the Von Mises theory. With regards to Fig. (10), the opening construction increased the average of Von Mises stresses inserted to tunnel lining, especially around the opening. The significant point in this stage is the effect of the steel structure, which prevents the tunnel from collapse after the opening construction. According to Fig. (10), the maximum stress value occurs at the corners of the opening.
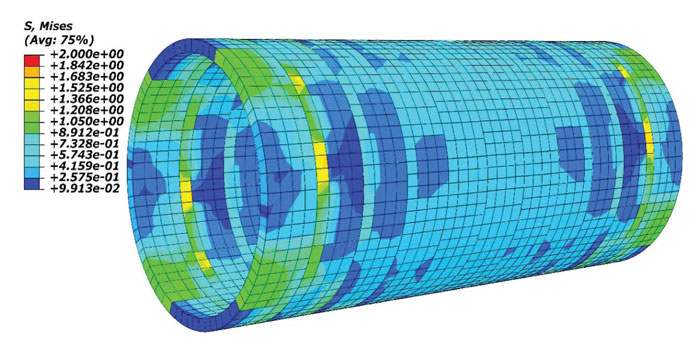

The maximum value for Mises stress in the segmental lining is about 4.5 MPa, which happened at the corners of the opening. It shows that the forces caused by opening construction are transferred to the segmental lining directly, and the areas around the opening are the critical zones.
3.1. Steel Frame and Bolts Bearing Capacity Control
3.1.1. Steel Frame
According to I.T.A standard [29], the allowable stress for ST37 Steel is calculated from the following relations:
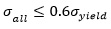 |
(6) |
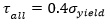 |
(7) |
The yield stress for ST37 Steel is about 235 MPa. While based on Eq. 5, 6, the allowable tensile stress should be lower than 140 MPa, and the allowable shear stress should be considered under 94 MPa.
3.1.2. Steel Bolts
The ultimate tensile stress for high strength bolts is 784 MPa. Whereas, the allowable tensile and shear stresses can be calculated from the following equations:
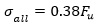 |
(8) |
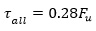 |
(9) |
The allowed tensile and shear stresses for the steel bolts are 298 MPa and 219 MPa, respectively. The Mises stress induced in the steel frame after the opening construction is presented in Fig. (11a). The maximum amount of inserted stress is 157 MPa, which happens at the corners of the steel frame like the stress distribution in the tunnel lining. Due to the high strength of the bolts, the stress distribution around the bolt location in the steel frame is lower than in other areas. The other critical areas in the steel frame are the centers of the vertical edges. Therefore, based on the risky zones in the steel frame, the following results would be concluded:
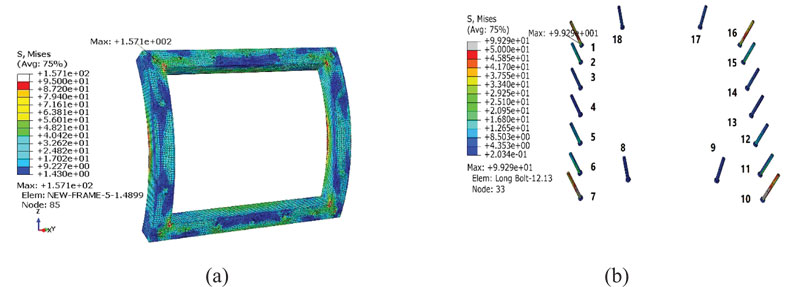
a. The steel frame resists against the opening in corners.
b. The steel frame resists against the bending of its vertical edges (opening of the longitudinal joints of cross-passage).
Fig. (11b) shows the induced stress in the steel bolts. Based on the mentioned criteria, the maximum stress in the bolts is lower than the allowable stress.
As discussed before, the maximum stress in the segmental lining occurs at the opening corners. Based on Fig. (11), bolts number 1, 7, 10, and 16 experience higher stress value than the other bolts. It also shows that the movement of the opening corners is more than the other zones.
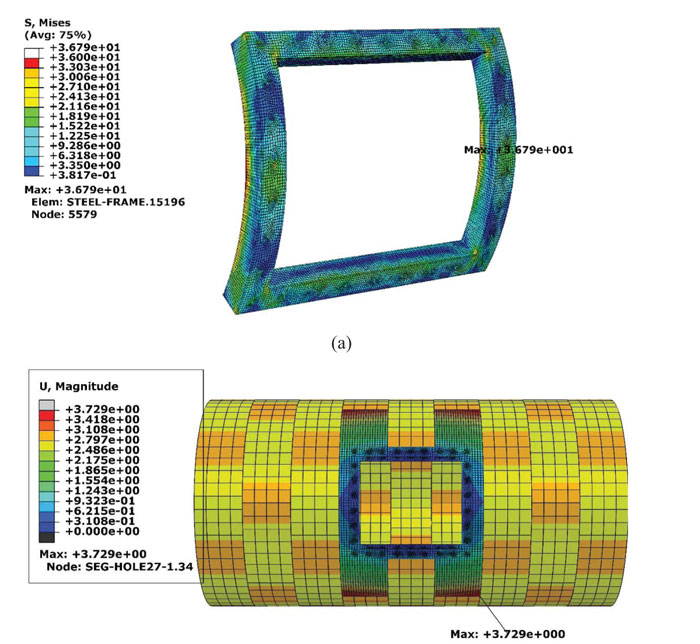
To improve the efficiency of the temporary support system, the number of steel bolts was increased up to 30. Fig. (12) shows the final state of the steel frame with 30 bolts. Regarding Fig. (12), the maximum stress in the segmental lining is 11 MPa, which occurs in the corners of the opening with 30 bolts. By increasing the number of steel bolts, the maximum value of stress-induced in the segmental lining was decreased to about 63 percent.
Fig. (13a) illustrates the distribution of the Mises stress in the steel frame in 30 bolts case. The maximum stress is around 36.8 MPa, and it was decreased to 76% compared to 18 bolts mode. Therefore, based on the newly obtained results, the number of bolts and the regular arrangements significantly affect the stress distribution in the tunnel lining and support system. Steel bolts are the main elements that carry the applied load from the segmental lining and transfer it to the frame. The maximum stress in the bolts occurs in their roots because of the exerted bending moment. Its value is equal to 40.7 MPa, which has decreased down to 59 percent. Displacements of the tunnel lining have displayed in Fig. (13b). The maximum movement around the opening is equal to 3.73 mm, which is about 62.7% lower than the case of 18 bolts.

A joint opening is one of the most critical parameters in the structural behavior of tunnel linings. As discussed before, the joint opening plays a vital role in lining failure. Therefore, it should be considered as a fundamental parameter in calculations. In this study, the effect of cross-passage construction on the opening of longitudinal joints has been investigated in both modes. In the following, the opening of the longitudinal joints is investigated based on the presented pattern (Fig. 14).
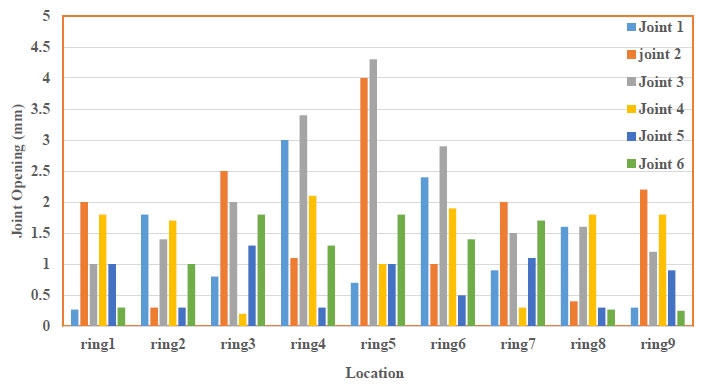
Due to the segment's staggered arrangement in the segmental tunnel lining, the pattern is presented for odd and even rings. The first and the last rings are omitted because of the boundary condition's effects. In the 18 bolts mode, values of opening displacement of the longitudinal joints for middle rings are presented in Table 3 and Fig. (15).
| Ring 9 | Ring 8 | Ring 7 | Ring 6 | Ring 5 | Ring 4 | Ring 3 | Ring 2 | Ring 1 | |
| 0.3 | 1.6 | 0.9 | 2.4 | 0.7 | 3 | 0.8 | 1.8 | 0.27 | Joint 1 |
| 2.2 | 0.4 | 2 | 1 | 4 | 1.1 | 2.5 | 0.3 | 2 | Joint 2 |
| 1.2 | 1.6 | 1.5 | 2.9 | 4.3 | 3.4 | 2 | 1.4 | 1 | Joint 3 |
| 1.8 | 1.8 | 0.3 | 1.9 | 1 | 2.1 | 0.2 | 1.7 | 1.8 | Joint 4 |
| 0.9 | 0.3 | 1.1 | 0.5 | 1 | 0.3 | 1.3 | 0.3 | 1 | Joint 5 |
| 0.25 | 0.27 | 1.7 | 1.4 | 1.8 | 1.3 | 1.8 | 1 | 0.3 | Joint 6 |
| ring1 | ring2 | ring3 | ring4 | ring5 | ring6 | ring7 | ring8 | ring9 | |
| Joint1 | 0.05 | 0.5 | 0.06 | 0.78 | 0.1 | 0.87 | 0.1 | 0.7 | 0.1 |
| Joint2 | 0.5 | 0.07 | 0.8 | 0.1 | 0.9 | 0.15 | 0.4 | 0.1 | 0.89 |
| Joint3 | 0.1 | 0.36 | 0.6 | 0.8 | 1.06 | 0.67 | 0.35 | 0.6 | 0.05 |
| Joint4 | 0.7 | 0.4 | 0.03 | 0.5 | 0.2 | 0.5 | 0.08 | 0.4 | 0.6 |
| Joint5 | 0.3 | 0.06 | 0.6 | 0.034 | 0.25 | 0.09 | 0.2 | 0.032 | 0.1 |
| Joint6 | 0.09 | 0.3 | 0.8 | 0.3 | 0.64 | 0.45 | 0.34 | 0.04 | 0.05 |
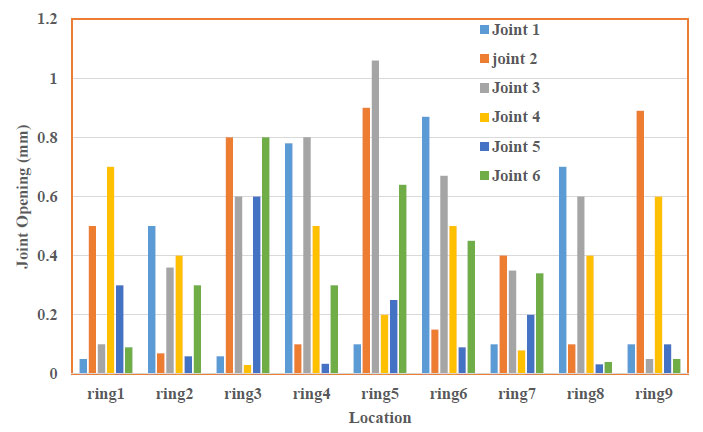
The maximum value of joints opening belongs to the closest rings to the cross-passage (rings 4, 5, and 6). The maximum opening value is 4.3 mm in joint No.3. Table 4 shows the joints opening after the reinforcement of the support system (30 bolts mode). According to Fig. (16), the reinforced supporting system with 30 bolts reduces the joint's opening down to 75 percent for the maximum amount. As mentioned before, the opening of the joints has a direct effect on stress and displacement induced in a frame. Therefore, in each joint, the higher opening causes significant stress and displacement in the frame.
CONCLUSION
In this research, a 3D simulation using the finite element method is performed. In the 3D simulation, the effect of opening construction in the segmental concrete lining and a temporary support system was analyzed. Based on the results of numerical analysis, most of the stresses on the segmental tunnel lining occurred around the opening span. Excavation of the cross passage increases the average stress-induced in segments. The induced stress in the steel frame is five times higher than the maximum induced stress in segments. As a result, the main role of the steel frame is to resist the opening of the longitudinal and circumferential joints around the gallery. The main resistance of the steel frames have against the openings, the fewer stress transferees to the segments; therefore, the stability of the tunnel is ensured. The steel frame is connected to the segmented frame by the steel bolts. Due to the resistance against the steel frame displacement, these bolts endure the stresses caused by the bending moment. The bolts in four corners of the frame experience the most stress. According to the outcomes, the stress magnitudes in bolts are in an acceptable range. To control the load-bearing capacity of the steel frame, the stresses created in the frame exceed the allowable stress for ST37 steel, and it is necessary to use ST52 steel. The maximum movement created by the opening in the concrete lining is equal to 5 mm around the opening. The maximum displacement of the steel frame happens at both sides equal to 8.6 mm. Also, minimum displacement occurs in the frame's top front.
The opening of joints in the segmental lining is another consequence of the gallery excavation, which has a reverse relationship with support system loading capacity. The average opening value of the joints before the gallery excavation is about 0.5 mm, which increases to 4 mm after the opening construction. By strengthening the steel frame, the results can be improved to a desirable level. In this research, this was accomplished by increasing the number of bolts. With the increase of bolts from 18 to 30, induced stress in the steel frame and bolts decreases to 76 and 59 percent, respectively. The maximum displacement in the segmental lining and the maximum opening value of the joints declines to 62.7 and 75 percent, respectively. By increasing the number of bolts, the average load in each bolt decreases. The uniform distribution of stresses and displacements in the steel frame confirms the improvement in designing the temporary support system and increases loading capacity.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


