All published articles of this journal are available on ScienceDirect.
Geometry, Static, Vibration and Bucking Analysis and Applications to Thin Elliptic Paraboloid Shells
Abstract
A large number of references dealing with the geometry, static, vibration and buckling analysis of elliptic paraboloid shells exist in the literature. This review work attempts to organize and summarize the extensive published literature on the basic achievements in investigations of thin-walled structures in the form of elliptic paraboloids. Possibilities of elliptic paraboloids with reference to machine-building and construction designs and to the apparatuses used in theoretical physics are briefly considered. The geometric part of the review is extended due to consideration of optimization of surface’s sizes, researches of representation of a surface on the plane and introducing bibliographic material on fractal geometry. Several existent analytical and numeral methods of calculation of the examined shells on durability give a possibility to choose one of the methods for the solution of new two-dimensional or three-dimensional tasks. Geometrical researches, approximation and bending of elliptic paraboloid surfaces, research of the stress-strain state of shells by analytical and numerical methods, natural and forced vibration of a shell, forming and setting of surfaces, application of shells in the form of elliptic paraboloids are the main problems which are considered in this review.
1. INTRODUCTION
Thin-walled shell structures have found the wide application in all branches of human activity. It is shown in many scientific-and-technical publications of architects, scientists, and mechanical engineers. The interesting information on the history of building and design of thin-walled space structures and on the future of special structures are presented in a manuscript of R. Bradshaw, D. Campbell, M. Gargari, A. Mirmiran, and P. Tripeny «Special Structures: Past, Present, and Future» [1] devoted to the 150th Anniversary of American Society of Civil Engineers. They write: “From the Georgia Dome in Atlanta, the Livestock Pavilion in Raleigh and Madison Square Gardening New York to the Olympic Stadium in Munich, and from Pontiac Silverdome in Michigan to the Sydney Opera House in Australia and Haj terminal in Saudi Arabia, special structures are landmarks and testimonials to the achievements of the structural engineering profession”. The same authors mark that “at present, shells have lost their popularity to their heyday in the 1950s and 1960s, when architects eagerly adopted them as a new mean for artistic expression. …. There are signs, however, that shells are attracting interest among the new generation of architects and engineers”.
The application of new shapes in the architecture of spatial shell structures is the second motive of regaining of their former popularity. The Department of Strength of Materials and Structures of RUDN University (Russia, Moscow) created a data bank of more than 500 surfaces [2]. But only 5% of existing forms have found real application. That is why, the publications of analytical and bibliographic reviews devoted to geometric and strength investigations of shells would be useful addition to monographs and scientific manuscripts on the proper theme. The reviews devoted to analysis, design, and application of shells in the form of cylindrical surfaces with non-circular cross-section [3], in the form of hypar [4], conoid [5], helical [6], torse [7], and spherical [8] surfaces, in the form of three-axial ellipsoids and ellipsoids of revolution [9], paraboloid of revolution [10], in the form of one-sheet hyperboloid [11] are available for researches. The listed shells have found wide spread application in building, mechanical engineering, shipbuilding, and in aircraft construction.
The reinforced concrete elliptic paraboloid shells, examined in this review, are used mainly in civil engineering because concrete is the most widely used material in large-span shell construction [12-15]. Grid shell systems are known too [16-19]. A variety of elliptical and parabolic dome type structures are used in important aerospace and civil structural systems [20] such as vehicles, stadium covers [16, 18], exhibition halls [12], auditoriums [21] and museum halls, as a road bed from shell panels [15]. However other materials are also used such as welded steel plates, metal decking, multiple layer timber decks, fiberglass- reinforced plastic, and so on. As an example of the application of elliptic paraboloids in mechanical engineering, one can present a modernized centrifugal mixer of powder materials declared in a patent Nº 51-167-99, 27.11.2003, RF. This mixer has inside a structure in the form of an elliptic paraboloid. In a patent Nº 2444690 (С2), 10.04.2011, RU «Water catch», the application of a breaking element in the form of elliptic paraboloid is patented. A nuclear energy plant for distillation and radiation-and-thermal cracking contains an outer circular shell of active zone in the form of an elliptic paraboloid (a patent Nº 2116330, 29.07.1998, RU). One may point out to the problem on pressure of a punch in the form of elliptic paraboloid on elastic body. Additional information on this problem will be given in the Part 8.
It should be noted that laminated composite stiffened elliptic paraboloid shells with cutout are found in many applications in the aerospace and naval construction industries.
In some experiments on theoretical physics, elliptic paraboloid fragments form focusing mirrors of resonator [22]. De Padova, et al [23] described antennas (radars) in the form of elliptic paraboloids. Other authors offer to use the examined surfaces for car headlights, in solar stoves, and in radio relay stations. An indirect technique of least-squares fitting of the elliptic paraboloid mesh reflector in 3D data is presented in [24]. Abramova and Abramov [25] study the complex deformation field on the fractal elliptic paraboloid in the multilayer nanosystem.
Till 1976, geometry of elliptic paraboloids, the investigations on stress-strain state of elliptic paraboloid shells, and applications of them have been presented in detail in a monograph [26]. Later, a manuscript [27] with 106 references was published and it became a base for the review presented. In preparing of this review, the authors used materials published in scientific and technical journals and proceedings, and studied monographs, reports of scientific conferences, and other scientific and technical literatures mainly for the period 1970-2016.
2. THE METHODS OF FORMING AND DEFINITIONS OF ELLIPTIC PARABOLOIDS
An elliptic paraboloid is an unexclusive non-central surface of the second order. In a right-handed Cartesian system of coordinates it has the canonical equation:
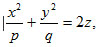 |
(1) |
where 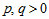 , (Fig. 1). Assume p = q then an elliptic paraboloid will degenerate into the paraboloid of revolution. Structures in the form of paraboloids of revolution will not be examined in this review. Review information on stress-strain analysis and application of shells in the form of paraboloid of revolution is given in [10].
, (Fig. 1). Assume p = q then an elliptic paraboloid will degenerate into the paraboloid of revolution. Structures in the form of paraboloids of revolution will not be examined in this review. Review information on stress-strain analysis and application of shells in the form of paraboloid of revolution is given in [10].
A plane z = h < 0 doesn’t intersect an elliptic paraboloid, a plane z = h = 0 has one common point with the paraboloid. The horizontal plane z = h > 0 intersects a paraboloid along the ellipse with semi-axes 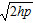 and
and 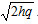 . All ellipses are similar each other, they have the same ratio of semi-axes
. All ellipses are similar each other, they have the same ratio of semi-axes 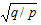 . A plane у = с intersects a paraboloid along the parabola with a focal parameter р and with the pick in the point (0, с, с2/(2q)). A plane х = b intersects a paraboloid along the parabola with focal parameter q and with the pick in the point (b, 0, b2/(2p)). The cross sections made by the planes у = 0 and х = 0 are principal parabolas accordingly x2 = 2pz, y = 0 and y2 = 2qz, x = 0 of the paraboloid. All these parabolas are open in the same direction. Elliptic paraboloid does not contain any straight line.
. A plane у = с intersects a paraboloid along the parabola with a focal parameter р and with the pick in the point (0, с, с2/(2q)). A plane х = b intersects a paraboloid along the parabola with focal parameter q and with the pick in the point (b, 0, b2/(2p)). The cross sections made by the planes у = 0 and х = 0 are principal parabolas accordingly x2 = 2pz, y = 0 and y2 = 2qz, x = 0 of the paraboloid. All these parabolas are open in the same direction. Elliptic paraboloid does not contain any straight line.
Elliptic paraboloid can be given as:
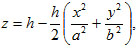 |
(2) |
where h is a surface sag. The plane z = 0 intersects an elliptic paraboloid along the ellipse with semi-axes 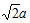 and
and 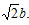
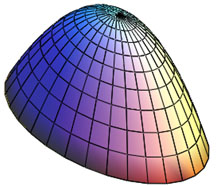
The parametric equations of elliptic paraboloid can be written in the following form (Fig. 2):
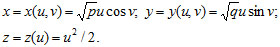 |
(3) |
Coefficients of the fundamental forms in the theory of surfaces
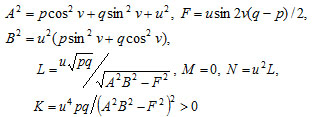 |
show that curvilinear coordinates u, v are non-orthogonal 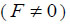 but conjugate (М = 0) coordinates. Assume
but conjugate (М = 0) coordinates. Assume 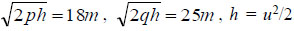 , where h is the surface rise, then we shall have a surface of the dome of the Basilica of St. Lawrence (a minor basilica of the Roman Catholic Church) located in downtown Asheville, North Carolina. The basilica was designed and built in 1905 by Spanish architect Rafael Guastavino along with his fellow architect R. S. Smith and the surrounding Catholic community of Asheville, North Carolina.
, where h is the surface rise, then we shall have a surface of the dome of the Basilica of St. Lawrence (a minor basilica of the Roman Catholic Church) located in downtown Asheville, North Carolina. The basilica was designed and built in 1905 by Spanish architect Rafael Guastavino along with his fellow architect R. S. Smith and the surrounding Catholic community of Asheville, North Carolina.
An explicit equation of a surface (1) may be transformed into parametrical equations (Fig. 1).
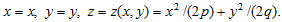 |
(4) |
These parametrical equations show that elliptic paraboloid is a surface of translation and formed by movement of one main parabola along another. This method was used in [28] for automatic modeling of single layer elliptical parabolic latticed shell. If directing and generating parabolas have the same focal distance, i.e. p = q, then one will have a paraboloid of revolution. There are innumerable set of nets of translation.
It is possible to use the following vector equation:
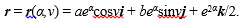 |
(5) |
This surface is attributed to isothermal conjugate coordinates α, v (L = N; M = 0).
Parametric equations of an elliptic paraboloid in lines of principal curvatures u and v can be written in the following form (Fig. 3).
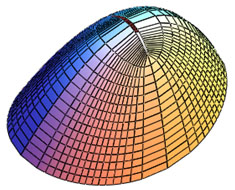
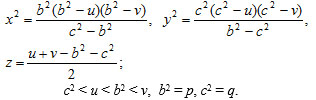 |
(6) |
The problem appearing in the process of forming elliptic paraboloid surface by a method of running contact attracted the attention of Stepanov and Belkin [29].
The additional information on geometry of elliptic paraboloids is presented in [26].
2.1. Additional Information on Possibility of Elliptic Paraboloid Surfaces
Affine-and-minimal surface is a surface with zero mean affine curvature. By contrast to ordinary minimal surfaces consisting of saddle points, an affine-and-minimal surface can contain elliptical points. So, an elliptical paraboloid consists of all-elliptic points but this is an affine-and- minimal surface.
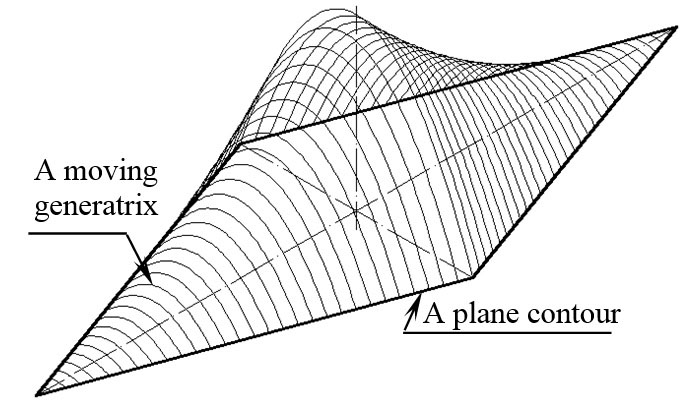
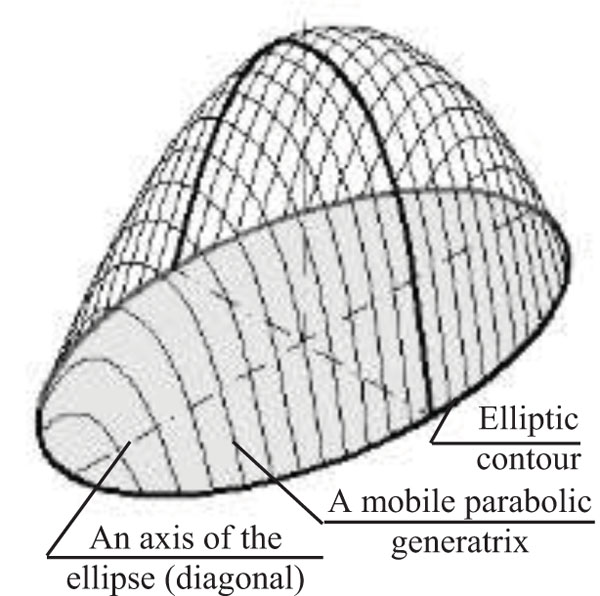
Surfaces of diagonal translation are formed due to translation of a plane curve along a directing curve so that in the process of sliding of a generating curve along the plane stationary contour, two symmetrical points of the generatrix have the contact with the contour (Fig. 4). Such surface may be constructed on a contour of arbitrary form. The surfaces formed on a contour with symmetry, such as circle, ellipse, square, and rectangle, are of the greatest interest. Sometimes, using a method of design of surfaces of diagonal translation, one may obtain well known surfaces. For example, assuming an ellipse as the plane contour and an axis of the ellipse as the diagonal and taking a mobile generating curve in the form of a parabola, one can obtain the elliptic paraboloid (Fig. 5).
Additional information on geometry of elliptic paraboloids is given in Hatiskatzi [30], where a method of construction of a line of intersection of the elliptic paraboloid with the cylinder is under consideration. Shovkoplyas [31] obtained the points of intersection of the elliptic paraboloid and the trihedral prism with the help of methods of descriptive geometry.
The motion of heavy material point on the elliptical paraboloid surface creates some exclusive periodic trajectories on its surface. It is of great interest in mathematicians. The problems of space rounding of smooth elliptic paraboloids under different angles of attack and slippage of a three-dimensional hypersonic flow of dissociating non- equilibrium air are considered in [32] where an approximate numerical method of solving the equations of a hypersonic, three-dimensional viscous shock layer is proposed.
Representations of surfaces on the plane are a typical task of the engineering geometry. It is formulated in the following way: for a given segment of the surface is required to find a flat area of an appointed form and from this form, the initial segment must be built by bending. The first step is to break the surface on the constructive modules, the borders of which will coincide with lines of seams. Next, dividing of modulus not belonging to developable surfaces into small fragments, limited by lines of horizontal sections, is used. By design, these parts can be approximated by developable surfaces with any given accuracy. However, researches have shown that the direct application of this algorithm is ineffective. Frolovskiy and Pavenko [33] offered to use additional limitations associated with the approaches of a theory of elasticity for prevention of the above-stated anomalies. An account of energy expenditures on the deformation of the starting surface is taken into consideration. In this case at the second stage, it is necessary to evaluate the energy expenditures on the deformation of the developable surfaces obtained at the first stage. As an example, a quasi-development of the elliptic paraboloid was adduced in [33].
Theocaris applies the elliptic paraboloid failure surface, constructed with the application of strength criterions, for the investigation of strength of composites, working in a three-axial stress state [34], polyurethane porous materials [35], for the evaluation of components of stress-strain state when continuous external load increases and provokes a change of material from elastic into plastic state and further till the value of the ultimate load [36]. Theocaris and Philippidis [37] affirm that geometrical parameters of the failure surface in the form of an elliptic paraboloid depend of quantity of strength anisotropy and strength properties of the materials.
It is known that the shape of a growing crystal can look like an elliptic paraboloid [38-40].
2.2. The Application of Elliptic Paraboloid Surface for Design of New Surfaces
Wavy chains with elliptic cross sections are formed by the translation of an ellipse along the straight line which is superposed with the coordinate axis Oz. In the process of the motion, the ellipse is lying in the plane perpendicular to an axis Oz. The values of semi-axes of the ellipses and their ratios are changed according to the law chosen.
A wavy chain with elliptic cross sections limited by an elliptic paraboloid is given by the following parametrical equations:
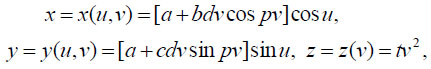 |
where a, b, c, p, t, d are the constants. Different forms of wavy chains with elliptic cross sections limited by the elliptic paraboloids are presented in Fig. (6). One may inquire about detailed information on these surfaces in the encyclopedia [2].
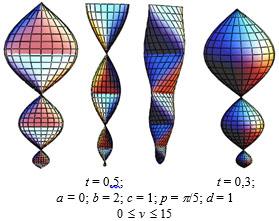
Interesting news on ancient military helmets in the form of elliptic paraboloid is adduced by Nikolaev [41].
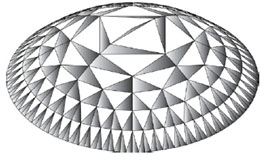
At the beginning of the 20th century, new mathematic structures were discovered. First, these structures were declared as pathological, somebody call them a gallery of “monsters”. In 1975, B. Mandelbrot introduced the word fractals for these shapes derived from the Latin “fractus” which means “break into pieces of random forms”. Now fractal geometry finds an application in urbanist architecture as the basic structures for the design of details of the same type in the process of transition from large scales to small. For example, a method of the design of grid or reticulated shell structures on the basis of elliptic paraboloid surface is given in [42] Fig. (7).
2.3. The Optimization of Geometrical Dimensions of Middle Shell Surfaces
A problem of optimization of shell may be formulated in two ways. One problem is working out the shell project with the most bearing capacity but with a given cost and the other problem is working out the shell project with the given bearing capacity but with a minimum cost. In the view of the authors of a paper [43], the second statement of the problem is of the most practical interest because the information about loads is starting data for designing.
A necessary result can be achieved with the help of rational material distribution under fixed geometrical parameters. There are ideas to use unequal reinforced prefabricated elements but with a point of view of technology, it is better to use shells gathered from the same elements. Redistribution of materials in a shell gives a possibility to decrease expenditure of the steel more than 8 times but it doesn’t top the general effect of optimization by 15-20 per cent because of the low content of the steel in shell. Varvak, Dekhtyar, and Shapiro [43] consider a problem of optimization of geometrical dimensions of the shells rectangular in a plan working in plastic stage under action of uniform surface load. The aim function is a shell cost including the running costs. In a calculated model, the simultaneous changing of shell thickness and its reinforcement with the constant coefficient of reinforcement is supposed. The problem was solved for two variants i.e. with taking running costs into account and without taking it into account. It was set up that running cost must be taken into account and that an elliptic paraboloid shell is the most comfortable one for the analysis.
A technique of reconstructing a class of quadratic surfaces, including elliptic paraboloids, from 3D data is presented in [44].
3. THEORETICAL STUDIES OF THE STRESS-STRAIN STATE OF ELLIPTIC PARABOLOID SHELLS
3.1. Momentless Shell Theory of Analysis
First, momentless shell theory was applied for the investigation of thin shells. Momentless theory of analysis of thin elliptic paraboloid shells was used by Fischer [45], Pavlović [46], Vlasov [47], and by other researchers [48-50]. Dulacska and Janko [48] affirm that results of momentless theory of shell in the form of an elliptic paraboloid subjected to uniform horizontal symmetrical load or inversely symmetrical load can be used for the shells, supported by boundary elements, rigid in bending and torsion. Lantukh [51] presents examples of analysis of momentless translational shells loaded by uniform load. For the solution of the problems it is necessary to use the tables of subsidiary coefficients presented in [52]. This method gives an opportunity to find firstly projections of normal forces Nxp and Nyp on the xOy plane and after that to obtain normal forces Nx, Ny in the shell. Lantukh [51] considers that the solution with the help of the tables is easier than the solution with using of a stress function. The volume of calculation cuts by half.
Results of many investigations show that elliptic paraboloid shells have the important advantage that the bending stresses are confined to narrow zones along the boundaries and are very small. Thus the membrane (momentless) theory provides often a good approximation for the stress condition of the shell [53].
3.2. The Shells on Rectangular Plane
A method of double trigonometric series is one of the wide spread methods of solution of system of linear differential equations with constant curvatures (kx = д2z/дx2; ky = д2z/дy2). Its principal propositions as applied to shallow elliptic paraboloid shell are presented in a reference book [54]. One supposed that a shell has simply supported edges and subjected to uniform loading.
A very extensive study of elliptic paraboloid shells with elastic edge members has been carried out by H.C. Shah [55] in 1960. The solution was obtained by using double trigonometric series. But Aass Asbjӧrn [53] holds that this solution for these boundary conditions is almost impossible for practical application. Double trigonometric series can be also used for the analysis of a shell with simply supported edges and eccentrically reinforced with ribs [56]. The known system of equations for shallow orthotropic shells was supplemented with the forth order differential operator which took into account the rigidity of the ribs and their eccentricity relatively the middle shell surface. It would be interesting to investigate an influence of value and sign of the eccentricity on the accuracy of a finite result. Later on in 1984 [57], the diagrams, illustrating the change of maximum flexure and bending moment of the shell, simply supported and rigidly fixed along the contour, depending on its rise, dimensions on the plane, and the height of stiffeners, were made.
Bending of an elastic elliptic paraboloid shell rested upon ribs was studied by Zmievskiy [58]. He used a Vlasov’s shallow shell theory and obtained a system of three differential equations in displacements. This system was solved with the help of a method of the Fourier’s finite integral transformation. The shell loaded by uniform distributed load was taken for the numerical example. The numerical results obtained were compared with results obtained with the help of a finite difference method and a finite element method.
A many-waved shell consisting of elliptic paraboloids was studied by Garanin [59]. A strain state was defined by the equation:
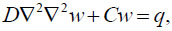 |
where D is the flexural rigidity of the shell, С = Eh/R2. Poison ratio was taken equal to zero. Garanin has taken into account three types of boundary conditions depending on the position of the shell in the many-waved covering. A solution was taken in a single polynomial series. A surface was given in a Cartesian coordinates. Membrane and bending theory of multi-span elliptic paraboloid shells was studied by Kashani-Sabet [60] too.
Fareed and Dawoud [61] applied a single polynomial series for analysis of a shallow translational shell rested on thin walls in two opposite edges and on an elastic foundation of Winkler’s type. Vasilenko [62] presented a solution of a problem on a stress state of an orthotropic thick shallow elliptic paraboloid shell. For a shell rectangular in plan with the edges free from normal load, a method of separation of variables was applied. So, the problem was reduced to one-dimensional boundary problem for a system of ordinary differential equations with piecewise-continuous coefficients. After that, this problem is solved by a numerical method.
Ansan [63] showed that Levy-type solutions for long cylindrical shells may be extended to elliptic paraboloid only for certain restricted boundary conditions. But Banerjee [64] proved that using of a stress function for analysis of elliptic paraboloid shells gives results not satisfying the fundamental equations for the equilibrium conditions.
3.3. A Point Support of Shell
Gambarova and Karini [65] analyzed the membrane and bending stresses in a uniformly loaded shell in the form of elliptic paraboloid on a rectangular plan with free supporting in the corners. They did it with the help of two absolutely different approaches. For the calculation of membrane stresses, a theory of A. Pucher for the semi-inverse problem was used. A special attention was paid to the behavior of zones siding with the corners where equilibrium conditions are satisfied at the expense of the membrane stress distribution under conditions that a deformed state is appeared from the solution of an inverse problem for a local area. A method of moire strips was used for the bending stress analysis. A picture of moire strips gave a possibility to obtain the elastic angles of turning and after that, the elastic curvatures with the help of differentiation and transversal displacements by integration.
Dekhtyar [66] demonstrated the optimal point supporting of shells on the basis of a kinematic method of the ultimate equilibrium theory. The covering is resting on four points. The corner fragments must be made from the same shell but turned over. A boundary effect in shells resting on the several columns is examined in [49]. Interesting results as applied to the problems of analysis of plates and shells resting on point supports under action of the local loads and the point disturbances were presented by Vidyushenkov [67]. He writes that numerical methods in these cases are ineffective and that is why analytical methods continue to play an important role for research of a stress-strain state of plates and shells resting on point supports.
3.4. Shells on Elliptic Plan
Many researchers used an asymptotic method of small parameter for shell analysis. A small parameter is selected depending on the structure of equations. It can have geometrical or physical sense. The presentation of a function in the form of the expansion in terms of a small parameter reduces an initial system of equations to an infinite system of the equations differing from each other only by the right parts. As a rule, a small parameter is chosen so that the first approximation has a nice calculation. In this case, all consequent approximations can be realized as more precise for the first one. First, Nash [68] has applied a method of small parameter for the analysis of an elliptic paraboloid shell. As initial equations, he has taken the equilibrium equations of K. Marguerre. But this work can be taken only as a statement paper because of its conciseness and inaccuracy.
Kozlov [69] made an analysis of a shallow shell on an elliptical plan taking as a small parameter a non-dimensional value of μ = f/a, where f is a rise of the shell, a is the semi-axis of a edge ellipse. The middle surface of the shell was taken in explicit form:
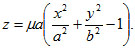 |
(7) |
Assume 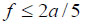 then
then 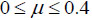 . Coefficients of the first fundamental form in the theory of surfaces were taken as A = B = 1, F = 0. A system of three differential equations of the shallow shell theory in components of an elastic displacement vector for thin shells given in Cartesian coordinates was derived in the limit of Kirchhoff’s hypotheses. After that, dimensionless coordinates ε = x/a, η = y/b were assumed. Due to the boundary conditions, parameters of an elastic displacement vector were taken as:
. Coefficients of the first fundamental form in the theory of surfaces were taken as A = B = 1, F = 0. A system of three differential equations of the shallow shell theory in components of an elastic displacement vector for thin shells given in Cartesian coordinates was derived in the limit of Kirchhoff’s hypotheses. After that, dimensionless coordinates ε = x/a, η = y/b were assumed. Due to the boundary conditions, parameters of an elastic displacement vector were taken as:
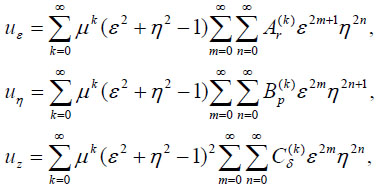 |
where μ is the small parameter, 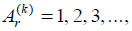
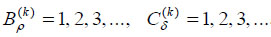 are the coefficients of decomposition. A shallow shell fixed along the elliptic contour was loaded by uniform vertical load Z = q, X = Y = 0. Kozlov [69] ascertained that it is enough to fulfill five or six approximations for practice calculations. Additionally, he showed that maximum values of displacements and bending moments for a shell examined in comparison with a plate less than 20%. The asymptotical method for the first approximation was applied for the analysis of a reinforced concrete dome of 7 m high. The support strengthened elliptic element has the spans of 45 × 63 m [70].
are the coefficients of decomposition. A shallow shell fixed along the elliptic contour was loaded by uniform vertical load Z = q, X = Y = 0. Kozlov [69] ascertained that it is enough to fulfill five or six approximations for practice calculations. Additionally, he showed that maximum values of displacements and bending moments for a shell examined in comparison with a plate less than 20%. The asymptotical method for the first approximation was applied for the analysis of a reinforced concrete dome of 7 m high. The support strengthened elliptic element has the spans of 45 × 63 m [70].
Srubshchik [71] has shown that the secondary edge effect phenomenon can hold when bending of elastic thin shallow shells in the form of an elliptic paraboloid under inner pressure takes place. Another approach was used by Slezinger and Barskaya [72] who investigated the influence of inhomogeneity on stress-strain state of a shallow shell with the middle elliptic paraboloid surface. The problem was considered in geometrically non-linear statement. The general equations were solved with the help of the Bubnov – Galerkin method.
The stress resultants and radial deflection of the portion of an elliptic paraboloid shell near its vertex subjected to a point load at its vertex were studied by Forsberg and Flügge [73]. The singular solutions to the homogeneous shallow-shell equations were expressed as power series.
Additional information on analytic analysis of elliptic paraboloid shells can be found in Refs [74, 75].
4. NUMERICAL METHODS OF DETERMINATION OF THE STRESS-STRAIN STATE OF ELLIPTIC PARABOLOID SHELLS
In many cases, usual analytical methods do not possess a sufficient community permitting to find solution for large quantity of shells of different geometrical shapes. By the way, boundary conditions don’t satisfy often the cases for which solutions can be found. Achievements of computer techniques ensure the opportunity of research of many problems by numerical methods. A method of nets, a finite difference energy method, and a finite element method are the most popular methods. One of the earliest works on element formulations of variational method for the analysis of elliptical paraboloid shells was reported by Aass Asbjӧrn [53] where the author proposed the solution satisfying the boundary conditions exactly but the basic equations only approximately. He has studied the shallow shells rectangular in plan for three types of boundary conditions. Goodman’s monograph [76] is one of the first serious works devoted to numerical analysis of elliptic paraboloid shells.
4.1. Grid Shell Models Simplifying an Analysis
Modeling of entire shallow shell structures with the help of a discrete element system is one of such methods [77]. Deformations of shearing and tensile are concentrated in the units. For elastic stadia of work, stresses – deformations relations were assumed as for a plane stress state. Equations describing the behavior of such model can be obtained and solved as a finite system of linear equations. Orthographic representations of vertical displacements, inner forces and moments for a shell in the form of elliptic paraboloid on the rectangular plan are presented in a paper [78]. The authors studied two cases just when all edges of the shell are simply supported or two opposite edges are simply supported but two other edges are free. Uniformly spread loading and a load defined to sinusoidal law was considered.
A thin shallow elliptic paraboloid shell on a quadrille plan was approximated by a grid shell model by Novak [79]. A problem was solved with the help of a momentless shell theory with loading by dead load.
4.2. A Method of Nets
A method of nets became popular long before appearance of computers but contemporary computational techniques became the most important stimulator of its subsequent development and wide application of the net methods for the solution of problems of engineering practice.
P.M. Varvak and L.P. Varvak [80] applied a method of nets for the analysis of a shallow elliptic paraboloid shell simply supported on a square plan. They assumed that the shell was under action of uniformly distributed load. An equation of the middle surface was taken in the following form:
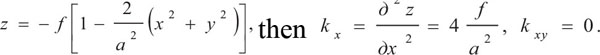 |
4.3. Finite Element Method (FEM)
Apraksina [81] carried out a comparative research of a stress-strain state of an elliptic paraboloid shell with the help of a theory of shallow and non-shallow shells given in arbitrary curvilinear coordinates. She applied FEM. The distribution of bending moments and normal forces in the principle cross-sections was studied for the diagonal section of the shell, square in a plane, with the ratio of total height to span equal to 1/5, 1/7, 1/15. A displacement vector was approximated with the help of bi-cubical polynomials with using of the node values of displacements and their derivatives in two directions.
For the analysis of elliptical parabolic domes, a shear deformable four-noded finite element based on a hybrid/mixed assumed stress is presented in a paper [20]. The element called improved Hybrid and Enhanced Shell element was developed for a general arbitrary orthogonal coordinate system. A detailed parametric study of anisotropic elliptical and parabolic shells of various configurations was carried out to investigate the effects of height ratios as well as layer lay-up schemes. A new flat quadrilateral shell element is presented in [82]. The results for uniformly distributed load pressure are obtained from both numerical and experimental work.
A triangular shallow shell rested in the corners is considered in a paper [83]. The shell edges are strengthened by the ribs. The authors show an opportunity to solve the problem by three methods. These are a method of separation of variables, a method of finite differences, and a method of finite elements. A rectangular finite element has twenty degrees of freedom. A method of separation of variables is preferred if a computer is of small capacity.
A new flat shell element was presented in [84] which can be used for practical engineering purposes.
4.4. A Finite Difference Method
In 1963, Pracash [85] studied a rectangular translational shell in the form of an elliptic paraboloid loaded by inner pressure. The shell edges were simply supported. Pracash reduced a governing equation to a Poison equation with a constant right part with the help of change of variables relatively the stress function. The equation obtained was solved with the help of a finite difference method. Later, Padilla and Schnobrich [86] used finite differences to treat elliptic paraboloid shells.
Novak Otakar [87] decided to study an influence of tangential displacements on the final result with the help of a finite difference method. He compared vertical displacements determined by an analysis with taking into account a hypothesis about equality of the tangential displacements to zero and without this hypothesis. It was assumed that the shell edges are rigidly fixed and the shell is subjected to a uniform distributed load. The results of analysis showed that maximum deviations of displacements, determined for an elliptic paraboloid due to an approximate analysis, constituted 15.3% in comparison with accurate results. And the mistaken increases as the shallowness increases. Deviation lies within the limits of 3.72% for a hyparshell, within the limit of 21.8% for a conoid shell. Before, he [88] derived a system of three equations in displacements for a shallow elliptic paraboloid on the square plan. Then orthographic representations of vertical displacements for two shells with the main dimensions of 18 × 18 m, the shell thickness of 6 cm and the shell rise of 2.5 m and 1 m were carried out. The load was assumed as uniformly distributed.
In 1981, Andrushkov and Rasskazov [89] obtained by a variational method a system of three equilibrium equations in displacements for a moment theory of non-shallow shells of arbitrary form defined in a Cartesian system of coordinates. The realization of the equations obtained was fulfilled for the elliptic paraboloid shells with a help of a finite difference method. They carried out the analyses of shallow and non-shallow shells. These results were compared with an analogous results determined with the help of the equations of a Vlasov’s theory of shallow shells and the moment shell theory in Cartesian coordinates written for a mixed method.
4.5. Large Strain Analysis
Stress-strain state of a thin shell in the form of elliptic paraboloid with taking into account plastic deformation was studied by Bozhanov and his colleagues [90]. Differential equations defining a work of a shell after elastic limit were obtained and their solutions were presented.
Some additional information for Part 2 and Part 3 of the review on a moment theory of analysis of thin shallow elliptic paraboloid shells can be found in Refs [79, 91].
5. EXPERIMENTAL STUDIES OF THE STRESS-STRAIN STATE OF ELLIPTIC PARABOLOID SHELLS
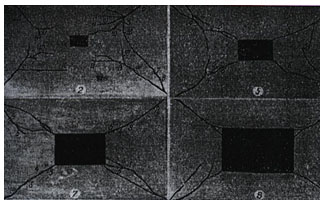
Theoretical investigations of bearing capacity of shallow shells with the openings of different forms and dimensions fulfilled by a kinematic method of ultimate equilibrium showed that small openings do not decrease bearing capacity but even can increase it. For control of the theoretical results obtained, Varvak and Dekhtyar [92] carried up the experiments with models of the free supported shallow reinforced concrete shells. They assumed a middle surface in the form of an elliptic paraboloid. The shell was of a constant thickness δ = 10 mm and with the dimensions in the plane of 2a × 2b = 120 × 80 сm. A shell rise was 2f = 90 mm and that is why f/b = 1/8.5. The reinforcement of the shell was fulfilled by the mesh from the annealed wire with a diameter of 0.74 mm placed with spacing of 20 mm in the middle of the shell thickness. The contour ribs were reinforced by the plane steelworks. The ribs were not jointed between themselves in the corners. All measurements were made by an indicator of clockwork type graduated to 0.01 mm. The measurements were applied for an accurate determination of the instant of limiting of bearing capacity of the shell. A disposition of progressing cracks on four models with the different openings is shown in Fig. (8). A uniform load was distributed on the whole shell surface. The opening was closed by the rigid element which passed the uniform load on its contour. For the calculation of a ultimate load, Varvak and Dekhtyar [92] determined the following formula:
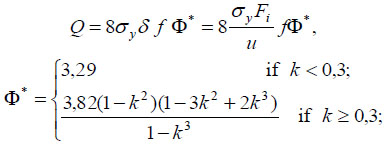 |
where σy is a yield limit of steel rods; Fi is the area of a cross-section of one rod of the mesh; u is the mesh spacing equaled in the both directions; k = a1/a; 2a1 is a dimension of an opening along a larger span; a is a larger span of the rectangular shell. The quantities of the real ultimate loads were compared with the calculation ultimate loads; the results were assembled into a table and presented in a graphic. An analysis of results given in [92] showed that bearing capacity of shallow shells doesn’t depend on dimensions of an opening and is practically equal for different openings with k < 0.3. Besides that, presence of openings of such dimensions doesn’t decrease bearing capacity of shells. The experiments corroborated the theoretical conclusions.
An experimental program of several different techniques in repair and strengthening of elliptical paraboloid reinforced concrete shells with openings was executed by Meleka et al [90]. The materials considered for strengthening are glass fiber reinforced polymers GFRP at different position of the shell bottom surface, steel strip and external tie. A computer program based on finite element techniques was used to study the behavior of these types of shells. Based on the research results, the authors [93] show that the using of shells without any openings is more efficient than using shell with a central opening as the failure load increased by about 14% and using of fiber reinforced polymer GFRP wrap is more efficient than using steel strips because GFRP provides higher rigidity and easier in applying. It is interesting that “use of fiber reinforced polymer GFRP wrap in diagonal direction is better than using it around the opening only as the failure load increased by about 10% and use fiber reinforced polymer GFRP wrap around the opening and external edges is better than using it around the opening only because failure load increased by about 20%”.
Some experimental results for the elliptical paraboloid shell under uniformly distributed pressure are given in [82]. The test model was made of aluminum and had a constant thickness of 2 mm with a plan rectangular projection of 880 mm by 400 mm. The model was free along the long edges. The experimental results were compared with theoretical results obtained by FEM.
Experimental researches of a large-scale model of the stationary covering of a stadium «Shakhtar» in Donetsk (Ukraine) are described by Horokhov et al [16] (Fig. 9). A model of the covering has a form of a truncated rod shell of positive curvature in the elliptical plan. A model surface can be defined by the equation:
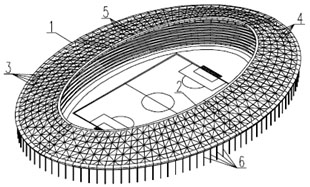
1 – external and 2 – internal index contours; 3 – radial, 4 – ring, and 5 – diagonal elements; 6 – external index contour columns
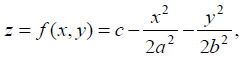 |
where the geometrical dimensions of the covering model in the plan are 2a×2b = 2,5×1,7 m with a rise of 170 mm. The covering model was tested in the elastic phase under static loads. The results of the experiments are given in a tabular form and in the form of the graphic representations of vertical displacements of the radial ribs located along the semi-axes of the elliptic plan. The real stadium has basic semi-axes with a = 123 m, b = 85 m and semi-axes of an upper elliptic contour with a1 = 93 m, b1 = 50 m. Testing the obtained data for goodness of fit was made with the help of a program complex «SCAD 7.27». The task was solved in geometrically non-linear formulation by a FEM. The dependences obtained during experimental studies well coincided with the data of analytical investigations that allowed using of it as a basis for elaboration of engineering procedure of calculation and designing.
6. STABILITY OF ELLIPTIC PARABOLOID SHELLS
6.1. Analytical and Numerical Researching Methods
The first results on the determination of critical pressure for a rigidly fixed thin shallow shell in the form of an elliptic paraboloid with the plane elliptic contour were derived by Pogorelov [94] who assumed that a bulge area was not small. With the help of a geometrical method he obtained the formula for the critical pressure:
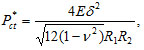 |
(8) |
where Е, ν, δ are correspondently Young’s modulus, Poison ratio, the thickness of the shell; R1, R2 are principal radii of curvatures of the elliptic paraboloid in the center of buckling. It should be noted that a formula (8) coincides with a classical formula for a critical pressure for a closed spherical shell with radius of 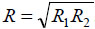 Babenko [95] declined a priory assumption about the form of a shell bulge and obtained the lower appraisal of the critical outer pressure:
Babenko [95] declined a priory assumption about the form of a shell bulge and obtained the lower appraisal of the critical outer pressure:
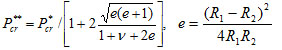 |
(9) |
also with the help of a geometric method. This critical pressure is attained in the case of a small area of bulge localized close by the ε- environment of one of elliptic paraboloid points placed outside the ε- environment of the rigidly fixed elliptic edge.
An approximate formula:
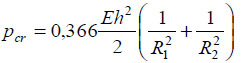 |
for the determination of critical pressure pcr for an elliptical paraboloid shell on the rectangular plan is presented in a book of Kollar and Dulacska [96]. An algorithm of numerical determination of critical surface load for a shallow shell on a rectangular plan with the spans of 20 by 10 m is presented in [97]. Nagy transformed a system of geometrically nonlinear equations into the form convenient for numerical integration by an iteration method with the application of a finite difference method. Stability of an orthotropic elliptic paraboloid with a fixed contour subjected to outer pressure may be examined by the Koiter’s method as it is shown in [98]. The equilibrium equations obtained by a variational method are solved by a Bubnov – Galerkin method. As an example, a layered shell was studied and the influence of the shell structure and the shell rise was evaluated. Babenko [99] derived the expressions for precritical momentless forces and the relations arising from the conditions of rigid fixation of a plane edge of a non-shallow shell subjected to uniform outer pressure. These relations gave a possibility to calculate uniformly the meanings of critical pressure taking into consideration the Babenko’s stability criterion of shells with the second order middle surfaces. B.I. Babenko illustrated his method by a numerical calculation of an elliptic paraboloid shell.
Qiang, Wei Che, and Huajin [100] simulate dynamic response of single-layer elliptical paraboloid latticed shells under impact based on rate-dependent isotropic hardening material model, master-slave contact point searching method and penalty function method. The effect of all kinds of parameters (such as span, rise-to-span ratio, and cross-sectional areas of members) is analyzed on the structural dynamic buckling. The results show that the displacements of characteristic nodes stain energy and total energy of the structure increase all of a sudden. The results of the stability analysis presented in [101] would be useful for the design and application of single-layer latticed shells with semi-rigid joints because the joints in the most spatial structures are semi-rigid. Parametric analysis of latticed shells was carried out using ANSYS with the help of finite element models. The behavior of single-layer latticed shells with semi-rigid joints is highly nonlinear and that is why the influence of the rigidity of a joint on the critical load of a single-layer dome has been studied by Huihuan Ma and his collegues [101].
Zingoni and Balden [102] report the results of a numerical study undertaken on the buckling behavior of lightly stiffened elliptic paraboloidal steel panels intended for use as long-span shuttering for lightweight concrete bridge decks, walkways and floors. A linear buckling analysis was carried out using the FEM program ABAQUS, to determine the lowest buckling loads (first mode solution) for the pressure loading and the gravity loading. The numerical comparisons show that for the lightly stiffened shallow elliptic paraboloidal steel panels in question, the linear buckling analysis predicts the first buckling load reasonably well for low aspect ratios (b/a = 0.2 and b/a = 0.4).
The buckling analyses for linear buckling, elastic buckling, and elastic-plastic buckling were performed in a paper [103]. The results of buckling loads were formulated based on two procedures for practical design use. One is explicit formula for elastic buckling loads using a knock down factor and the other one is an implicit expression for buckling loads interpreted as a column buckling strength in terms of generalized slenderness ratio. An efficient method for evaluating elastic-plastic buckling loads of two-way elliptic paraboloid lattice domes of single layer under vertical loads was proposed in [104]. The comparison of the evaluated buckling loads with those obtained from FEM elasto-plastic buckling analysis proves that the procedure is valid and efficient enough to be applied in design practice.
Graphite-epoxy multilayered elliptic paraboloid shell panels having rectangular planforms are widely used in various fields of aerospace because of their light weight, high stiffness, and strength. The thermomechanical postbuckling response of these shell panels was obtained by Maloy K. Singha et al [105] within the framework of FEM. Numerical results presented in this paper show the effect of temperature dependence of material properties on limit loads of shallow panels.
Bearing capacity of the elliptic paraboloid grid shell with semi-rigid joints is analyzed in [106, 107]. The influence of section of steel bars, rise-span ratio and initial imperfection on the bearing capacity is also investigated in these papers. The nonlinear buckling behavior of an elliptic paraboloid suspended dome structure of span 110m×80m is investigated in [108, 109] by introducing geometric nonlinearity, initial geometric imperfection, material elastic-plasticity and half-span distribution of live loads. The study shows that the coefficient of stable bearing capacity usually is not minimal when the initial geometric imperfection configuration is taken as the first order buckling mode.
Additional information on stability of elliptic paraboloid shells can be taken in [110-112].
Ballesteros [113] gave the information on the collapse of an elliptical paraboloid shell during the process of removing the formwork. The structure showed clear imperfections in the geometry and had construction defects.
6.2. Experimental Studies of Elliptic Paraboloid Shells
The results of experimental control of formulas (8) and (9) are presented in [114]. The elliptical paraboloid shells were made by pressing of the shallow spherical shells in specially manufactured contrivances. The shells underwent the deformations and took the form of a elliptic paraboloid with principal radii of curvatures R1, R2. The moment stresses appearing in the process of bending are very small and that is why they do not have an influence on value of critical load 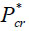 . The investigations showed that a formula (8) gives a critical pressure for weakened conditions of a rigidly fixed edge but a formula (9) answers the rigid fixing of a plane elliptic edge. The loss of stability of an elliptic paraboloid shell begins after appearance of a small hollow at the top of the shell as in a case with spherical shells. An installation for the investigation of after-critical deformations of shallow elliptic paraboloid shells rigidly fixed along an elliptical edge of the shell subjected to outer pressure is offered by Babenko, Koshelev, and Avedyan [115, 116] who tested a paraboloid of revolution. The shells for the testing have been made by a method of deposition of copper on shell by evaporation in vacuum. Loading by outer pressure was realized with the help of a method of pumping out of air from a space under the shell. The aftercritical unstable branches of pressure-deflection dependences in the shell top and values of the low critical loads determined in the experiments were compared with results of asymptotic solution of the proper shell theory equations.
. The investigations showed that a formula (8) gives a critical pressure for weakened conditions of a rigidly fixed edge but a formula (9) answers the rigid fixing of a plane elliptic edge. The loss of stability of an elliptic paraboloid shell begins after appearance of a small hollow at the top of the shell as in a case with spherical shells. An installation for the investigation of after-critical deformations of shallow elliptic paraboloid shells rigidly fixed along an elliptical edge of the shell subjected to outer pressure is offered by Babenko, Koshelev, and Avedyan [115, 116] who tested a paraboloid of revolution. The shells for the testing have been made by a method of deposition of copper on shell by evaporation in vacuum. Loading by outer pressure was realized with the help of a method of pumping out of air from a space under the shell. The aftercritical unstable branches of pressure-deflection dependences in the shell top and values of the low critical loads determined in the experiments were compared with results of asymptotic solution of the proper shell theory equations.
In his report, R.E. Row [117] presented a condensed account of the activities of the Department “Association on Cement and Concrete” (UK) and described the test of a one-tenth scale model of the elliptic paraboloid shell (1.45×1.45m, a thickness is 0.64 cm). This model copied a part of covering of a garage in Lincoln designed by Dr. Hajnal Konyi. This test was very important with a point of view of determination of possibilities of the shell models and elaboration of methods of loading and taking down of readings.
A shallow shell model of roofing of the Smithfield Poultry Market, London, UK, was used for the determination of characteristics of local loss of stability [118, 119]. The shell measures 68.6×38.12 m and its total height is 9.1 m. A model was made in a scale of 1:12 (5.22×3.25 m).
G. Franz [120] describes testing of shell models with a thickness of 3 mm made of several layers of glass fibers and epoxy resin. The shells were tested without thickening of the edges with resting on immovable supports (αk = 0.138), with thickening of the edges with resting on immovable supports (αk = 0.128), and with resting on the edges with opportunity of lateral displacement (αk = 0.32). All of the models were loaded by uniformly distributed load. The models were with the dimensions of 1200 by 600 mm in plan. The test results showed that the flexure coefficients of αk being a factor of a formula for the determination of a critical load:
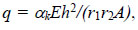 |
Coincide nearly with the theoretical coefficients of Karman and Mushtary – Surkin and also with experimental values of Schmidt. Here, A is an area of the shell surface, the shells have the edge beams and rest on the supports as membranes. The application of models for researching works is a useful addition for better understanding of the behavior of thin-walled structures.
7. FREE AND FORCED VIBRATIONS
Almost all existing literature is devoted to investigation of natural vibration. Only Duan X.N. et al [121] studied the influence of the effects of the vertical ground motion upon the latticed shell structure.
7.1. Analytical Research Methods
Natural vibrations of a shallow elliptic paraboloid on an elliptic plan were considered by Kozlov [122] in 1972. A surface equation was taken in the explicit form (7). A principle of Ostrogradskiy – Hamilton was used for the writing down of a functional for the subsequent application of a Ritz’s method. A problem on dynamic behavior of shallow shell on Winkler bedding under vertical seismic forces was under consideration in [123]. Fan Jiashen used equations of Vlasov’s technical shell theory for solution of which an apparatus of a theory of potential and Fourier’s trigonometric series were applied. A method presented may be applied for the investigation of behavior of shell under seismic load.
An interesting problem is examined in a paper [124], where sound pressure caused by vibrations of a square steel shell in the form of an elliptic paraboloid (a = b = 1 m)
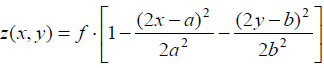 |
is assessed. The shell thickness is 0.002 m. A shallow shell possesses of inner viscous-elastic damping. The damping coefficient ε is equal to 0.001. The Voigt-Kelvin model of damping was assumed. The inertial components provoked the motion in the tangential directions of the shell middle surface are neglected in the model. Vertical vibrations of a shell are defined by normal displacements:
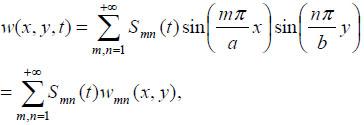 |
where Smn(t) are unknown functions of time and wmn(x,y) are the shape function for the (m,n)-th mode. Kozien and Niziol [124] consider that shallow shells are commonly used as constructional elements of heavy duty machines. The results of analysis show an important influence of the radii of curvatures of a viscoelastic shallow shell on dispersion of the pressure in a chosen control point in the acoustic surrounding medium. Natural vibrations of a body in the form of an elliptic paraboloid placed in a limited volume of liquid and vibrations of a level of this liquid are studied by Hisashi Hukuda [125] with the application of the quasi-Lame equation.
The Galerkin method coupled with integral transform method was applied by Yung-Tze Chen [126] for determining the natural frequencies of cracked shallow elliptic paraboloid shells simply supported on four edges.
7.2. Numerical Methods of Investigation
Dynamic analysis of shell structures can be solved efficiently by finite element method. Different computational models for laminated composites were proposed by researches. Modeling the shells of double curvature, Sahu and Datta [127] applied a finite element taking into account transversal deformations and inertia of rotation. A used method spreads a theory of dynamic transversal deformation with the application of the first approximation of Sandler to a problem of laminated composite doubly curved shells. After that, this problem was reduced to the theories of Love and Donnel by the use of tracers. Non-dimensional natural frequencies:
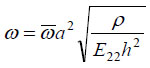 |
(a/b = 1; a/h = 100; E11 = E22 = 25; G23 = 0,2E22; G12 = G13 = 0,5E22; ν12 = 0,25) were determined for free supported shells in the form of sphere, elliptic and hyperbolic paraboloids for research of the effect of geometry of the shell and a quantity of layers of the composed shell. The obtained results give a good coincidence with analogues results presented in [128] where FEM was used also.
Free vibration problem of stiffened shells with different size and position of the cutouts was examined in [129] where natural frequency and mode shapes were studied. An eight-noded curved quadratic isoparametric finite element was used. The finite element model proposed in [129] can successfully analyze vibration problems of stiffened composite shells with cutout. It was noticed that for clamped shells the maximum fundamental frequency always occurs along the diagonal of the shell. Sarmila Sahoo [130] insists that the information available for vibration behavior of all common forms of both anticlastic and synclastic shells with cutouts is far from complete.
The Kriging algorithm [131] was developed in [132] to quantify uncertainties in natural frequencies of cantilever composite shallow doubly curved shells and its efficacy was compares with direct Monte Carlo simulation technique. An eight noded isoparametric quadratic element with five degrees of freedom at each node was considered in finite element formulation. Four layered graphite-epoxy symmetric angle-ply and cross-ply laminated composite cantilever shallow elliptic paraboloid shell with thickness of 5 mm was considered and it was observed that Kriging model can handle the large number of input parameters. The results obtained by employing Kriging models are found accurate with the results found by using direct Monte Carlo simulation.
8. PROBLEMS OF THEORY OF ELASTICITY
The mechanics of contact between deformable bodies is an important and actively developing part of continuum mechanics [133]. An asymptotic solution of the contact problem for a punch in the form of an elliptical paraboloid was obtained first by Poroshin in the case of thick elastic layer [134]. Pressure of elliptic paraboloid stamp on elastic body was studied also in [135-139]. It should be noted that the contact problem can be the subject of special review.
In this paper, we shall note only that a solution of the problem on pressure of an elastic press tool in the form of elastic paraboloid on elastic plate with small contact area can be found in [135]. An action of a press tool on a plate is modeled by an action of point force and moment. A problem of one-sided contact is solved by a method of asymptotic expansion and its solution was obtained on the base of L.A. Galin’s results of 1947th [140]. The moments ensuring a forward pressing of press tool were calculated and an equation connecting a press tool displacement with force acting on it was derived. Argatov [141] studied also pressure of a system of stamps in the form of elliptic paraboloids on elastic half-space. The asymptotic solution of the axisymmetric problem is written out in explicit form by Argatov too in [134]. Having analyzed contact pressures in cone transmissions, one can use a Hertz solution for a problem of contact of two elliptical paraboloids [142]. Korobkin [143] presented an exact solution of a problem on immersion of an elliptic paraboloid into incompressible liquid with different velocity.
The history of researches is detailed in a book [133].
9. EXAMPLES OF ERECTED AND DESIGNED SHELLS IN THE FORM OF ELLIPTIC PARABOLOIDS
The stone erections of a complex of Big Zimbabwe (Zimbabwe, Africa) produce a large impression on the visitors. One of these erections resembles the form of the elliptic paraboloid and made of unwrought stones without using of binding materials (Fig. 10).
Grid shell is a new type of single layer latticed shell. Glymph J. et al. [17] affirms that the principle of an evenly-meshed translation surface with different parabolas as generatrix and directrix was first realized with the roof over a courtyard in Rostock, Germany (Fig. 11). A parabola translating across another parabola perpendicular to it results in an elliptic layout curve and an evenly meshed net consisting of plane quadrangular mesh. Andrew Orton [144] also offers a method of forming of grid elliptical paraboloid shells.


The inner volume of the covered tennis court in Budapest (Hungary) was selected in the form of an elliptical paraboloid because this form was in keeping with the best conditions of play in tennis. The both playgrounds were covered by the same shells resting along short sides (18.75 m) on the massive walls but along long sides (39.10 m) on the arches. Design and static analyses were fulfilled under the direct leadership of St. Minihard. Own weight, snow load, and wind pressure were in view.
In Budapest (Hungary) a sport hall on an elliptic ground plan of 96 × 64 m was covered by a reticulated tubular shell structure having the form of an elliptic paraboloid (Fig. 12). Both functional and structural reasons postulated an elliptic ground plan. The columns of the dome structure are also tubes. The paper [18] outlines the development of the structure and some problems in the static analysis, describes the fabrication process, and shows some structural details.
An elliptic paraboloid covering for the hall of the Building of Fine Arts of Utkal University in Bhubaneswar (Orissa, India) has the dimensions of 24.83 by 21,6 m in plan [21]. A shell thickness is 88.9 mm and it becomes 127 mm near the contours. The edges rest on elastic reinforced concrete arches with tie-beams.
A shell over the building of Oklahoma State Fair Arena (USA) is a concave down elliptic paraboloid with dimension of 400×320 ft. (121.9×97.54 m) in plan. The shell was erected in 1965. The shell was made of precast prestressed reinforced concrete with stressing of the steel on the concrete. The factors showing an economy of the taken method of building of this shell are stated in [12]. An analysis of load-balancing method for design of an optimal shape of the shell surface under given load and with a given plan is presented in [13]. It was shown here that an ideal shape of the shell surface comes nearer to an elliptic paraboloid defined by the equation of x2/a+y2/b = cz. Prestressed concrete shell roof in the form of the 400-foot span elliptical paraboloid for Oklahoma State Fair Arena (Fig. 13) was designed with the help of consultant Alexander C. Scordelis, who was distinguished structural engineer.

A combinatory net-shell roof of Zhaoqing Gymnasium in the form of an elliptic paraboloid was erected in China [19]. The Qinyang Stadium is a key project of the Qinyang City. It used elliptical parabolic roof with long axis of 101.22 m, short axis of 72.39 m, and the height of 7.2 m. The authors of a paper [145] calculated and designed four structural schemes such as suspended dome, single-layer latticed shell, double-layer latticed shell, and rigid suspend-dome. Z.R. Jiang and his colleagues [108] think that suspended dome structure is a new kind of hybrid spatial structure. It consists of the upper single layer latticed shell and the lower cable-strut system.
A reinforced concrete dome covering of the Smithfield Poultry Market, architect T.P. Bennett and Son, engineer Ove Arup, in London (UK) was built in 1961-1963 on the spot of the old market building burnt in 1958. A new building was designed in the form of an elliptic paraboloid with the dimension of 68.6 ×38.12 m in plan, 9.1 m high, a shell thickness is 7.5 cm, a shell thickness in corners is 20 cm. A middle surface of the shell is defined by an equation z = (x/rx)2+ (y/ry)2 (Fig. 14). Having been inside, the visitors wonder and express an admiration with triumph of technical idea [14]. At the moment of erection, it was the largest thin-walled reinforced concrete shell. The shell was calculated with the help of momentless theory with the approximate accounting of the boundary bending moments. Detailed researches were carried out on a dome model on a 1:12 scale. Experiments lasted 6 months. A special attention was given to the estimation of its stability. Prestressed contour elements are rested on columns, but at a look from within, it seems that the shell is supported only in corners. This effect gives easiness to the whole building and assures good lighting inside. The dome was concreted on shutter from standard trapezoidal plywood boards of unitary curvature. The supporting woods were carried out from steel pipes. Concrete was placed against forms beginning from the corners in the direction of the dome top and reinforcement was carried out by two steel nets with the rods parallel to the shell edges. The additional oblique reinforcing bars were laid in the corners.

Danish architect J. Utzon offered to take the large sails in the Sydney Opera House in the form of the elliptic paraboloids but a project was done over again in 1966. The large sails were designed in the form of the spherical fragments. Danger of coming off decorative tiles because of differences of thermal deformations is one of the reasons of substituting of elliptic paraboloid form for spherical one.
In a Part 5 the authors mentioned already about the spatial covering of a stadium “Shakhtar” in Donetsk (Ukraine) in the form of a truncated elliptic paraboloid dome (Figs. 9 and 15).

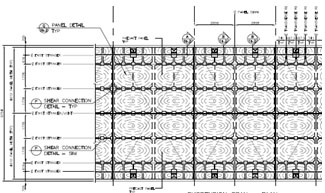
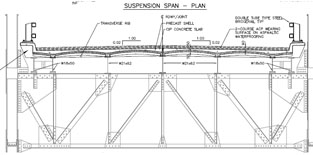
A firm «Alberta Infrastructure and Transportation» declared a competition for design of reconstruction and change of the road bed of the two-strip bridge of 500 m in length over a river Peace (Fig. 16). Dr. S. Balakrishnan [15] studied several alternative variants. The comparison was carried out with allowance for total weight of the structures used, their durability, fire-resistance, costs, and other indices. A variant of a road bed from shell panels of 2857.5 mm in length was considered as the best one (Fig. 17). Every panel contains four elliptic paraboloids which are united in the longitudinal and transversal directions by ribs of stiffness. The elliptic paraboloids have a minimal thickness of 100 mm and are thickened in the direction of the ribs. The thickness varies from 175 to 250 mm (Fig. 18). By the way, elliptic paraboloids do not require reinforcement with the exception of the steel reinforcement for preliminary stressing of the ribs in the both directions. Theoretical calculations of the panels were made by FEM.
G.V. Murashkin, S.M. Anpilov, and V.G. Murashkin [146] patented a method of decreasing shrinkage deformation in monolithic reinforced concrete coverings and the means for its implementation. They noted that monolithic reinforced concrete coverings being progressive in terms of economy and comfort possess, however, a number of shortcomings. A display of shrinkage deformation in monolithic reinforced concrete covering is a grave shortcoming reducing reliability of a structure and disturbing its continuity. Shrinkage deformations of concrete give rise to tensile stresses in concrete as a result of static indefinability of the ceiling but, on the other hand, due to the existence of steel-to-concrete bond.

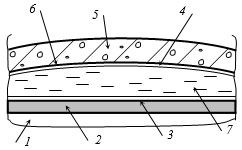
The outstanding architect and engineer E. Torroja told, that the shell, the durability of which was provided by its form mainly but not by strength of its material is the best shell. E. Torroja has a lot of followers. For example, Fomitsa and Tsyganenko [147] offered to take a middle surface of the reinforced concrete shell in the form of the 4th order translational surface [148]. The characteristic feature of this surface is the decrease of the curvature from a maximum in the center of a span up to zero near the contour beam elements. They showed that such shell is less deformable in comparison with an elliptical paraboloid and it survives 1.84 times the load at identical vertical displacements.
CONCLUSION
Although the hyperbolic paraboloid is the most popular type of shells, due to its attractive form and simple structure [2], many researchers carry out investigations in the field of strength, vibration, stability, and application of elliptic paraboloid shells that are also very attractive from an architectural point of view.
The thin-walled and thick-walled shells considered in this review serve as the dome type structures in mechanical engineering. For example, they are used in aerospace systems, nuclear energy plants, in some experiments on theoretical physics, and so on.
The authors have tried to assemble various investigations on this widely applied class of elliptic paraboloid shells. The review presents a brief survey of analysis of elliptic paraboloid shells with references. The authors hope that the presented materials can reduce literature searches and can point to future research. The most of mechanical engineers prefer popular finite element analysis programs demanded by modern practice. But it would not be rational to rely only upon this method and, that is why, the author presented not only numerical but and analytical methods of calculation too. Anton Tedesco, the outstanding North-American-reinforced-concrete-shell-builder said: “Young engineers are often perfect in using computers, but they don’t know where to put the comma. It’s not the computer which produces ideas. Let us not throw away the pencil and the slide-rule” [149].
This review may be useful not only for specialists in strength analysis and the design of shells, but also for teachers because the modern training of engineers must include an acquaintance with modern design, strength analysis, and erection of shells of complicated form. “It is necessary, however, for academic programs to recognize the unique features of special structures and devote parts of the curriculum to discuss their analysis, design, and construction” [1].
Having examined the situation on rising interest to the shells, the Department of Strength of Materials and Structures of Peoples’ Friendship University of Russia decided to organize the magistrates “Architecture, Geometry, and Strength Analysis of Large-Span Space Structures”.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This review paper was financially supported by the Ministry of Education and Science of the Russian Federation on the program to improve the competitiveness of Peoples’ Friendship University (RUDN University) among the world’s leading research and educational centers in the 2016-2020.
The authors also wish to express their appreciation for the financial support provided by the “Véréchaguine A.R.” Ecole Supérieure de Génie Civil (ESGC - VAK), Benin.


