All published articles of this journal are available on ScienceDirect.
Modelling the Dynamics of Masonry Structures with Discrete Elements
Abstract
Block models have been shown to provide a realistic representation of the behavior of many types of masonry structures under static and dynamic loads. When the strength of the units is such that movements along the joints govern the behavior, it is acceptable to make the simplifying assumption that blocks act as rigid bodies. This assumption is particularly useful when dealing with seismic problems, for which the computational times for time domain analysis may be substantial.
In this paper, the application of discrete element models for dynamic analysis of masonry structures is addressed. The emphasis is on the seismic behavior of block stone masonry, but the treatment is general to cover other types of masonry. First, the assumptions involved in the choice of a block representation are discussed, stressing in particular the case of rigid block models. Numerical issues are examined, including contact models, calculation of natural frequencies, time stepping algorithms, damping and boundary conditions.
A review is presented of modeling examples published in the literature for various types of masonry structures. The choice of numerical representation and its main features are discussed for each case.
1. INTRODUCTION
Earthquakes pose a major threat to unreinforced masonry, in particular historical structures are highly vulnerable. Numerical models are presently the best tool to analyze the behavior of these structures under seismic loads or other types of dynamic input. Comparisons with experimental evidence, whether shaking table tests, or structural monitoring data obtained during seismic events, have allowed the progressive validation of the new numerical tools. These may nowadays be used with more confidence in the prediction of dynamic behavior and safety assessment studies.
Given the complexity of masonry behavior, nonlinear analysis tools need to be employed. Among these, discrete element models are one of the most powerful options, as reported in surveys ofpublished works [1], which demonstrate the ability of polyhedral block representations to reproduce key aspects of the deformation and failure of masonry.
In seismic analysis, the main applications of discrete block models have dealt with relatively simple stone masonry structures, for example, the column-architrave systems of classical monuments. Extension to larger and more complex constructions raises a number of issues, ranging from the conceptual level to the strictly computational. The present paper addresses some of these issues, presenting a discussion of the available options and the requirements for proficient use.
The fundamentals of discrete element modeling, in the context of structural masonry, are briefly reviewed in the next section. The particular issues related to dynamic analysis are then presented. Finally, several examples taken from published case studies are examined, in order to illustrate the model capabilities and the various issues that may arise in applied studies.
2. DISCRETE ELEMENT MODELS
2.1. Macro and Micro-Modeling. Types of Discrete Elements
There are two basic alternatives to approach a complex material such as masonry: equivalent continuum idealizations (“macro-modeling”) and discontinuum idealizations (“micro-modeling”). Both have been applied successively in many projects and have their preferred domains of application, as discussed in the literature (e.g. [2]). Discontinuum or micro-models represent explicitly the blocks of intact material and the joints between them. Different numerical options have been employed for this purpose, namely involving joint or interface finite elements and various types of contact formulations, as discussed below.
One of the strong points of discontinuum models is the representation of failure modes, which in masonry structures are generally governed by the location and orientation of the joints. Stone block masonry may be idealized very naturally with a numerical block model. However, except for simple structures or components (pillars, arches, etc.), a one-to-one relation between physical and numerical blocks cannot be maintained. The model would become excessively complicated and time-consuming, not just in computer run-time, but also in data preparation and analysis of results. Therefore, block sizes larger than the real ones are often used. As a consequence, the nature of the numerical model as an idealization of the real construction becomes even more apparent: for example, the mechanical parameters assigned to blocks and joints have to be consistent with the underlying modeling assumptions.
Irregular masonry is commonly idealized with continuum macro-models. A radically different approach is available in the form of a special class of discrete elements, the bonded-particle models, already used in the study of fracture of rockor concrete. These very detailed representations are still computationally demanding, particularly in 3D, and are more suited for fundamental research work, so they will not be addressed in the present paper Block models may also be employed to simulate irregular masonry, given their ability to follow failure mechanisms involving substantial sliding and fracture opening. In this approach, a fictitious joint pattern is created that can encompass the foreseeable modes of collapse. Joints are assigned the strength of the intact material, and only represent the potential fracture surfaces of masonry material. Ideally, more than one joint pattern should be tried to assess the generality of the results.
2.2. Rigid and Deformable Block Models
In rigid block models, all the system deformation is lumped at the joints. For hard stone block masonry, this idealization is physically defensible. But, in other cases, rigid block models are used for their computational advantages. The examples in section 4 show that a rigid block model may simulate reasonably well the dynamics of masonry pillars and walls.
Deformable block models are conceptually equivalent to finite element micro-models. The designation “discrete-finite elements” is also used by some authors. Each block is composed by an internal finite element mesh.
Structural failure of masonry under dynamic loads is more conveniently analyzed with explicit time stepping algorithms. As discussed below, the presence of stiff elements or joints renders the analysis computationally inefficient. In this context, a hard stone block is preferably represented by a rigid block, with its deformability added to the joints, if necessary. On the other hand, for the case of a soft material, to assign the global deformability to the blocks and make the joint very stiff is also not recommendable. Ideally, from a numerical point of view, deformable block models should embody a partition of system deformability between intact material and joints that is not too contrasting.
The use of simple elements (low order triangles and tetrahedral) in deformable blocks has, first of all, the advantages of automatic mesh generation for arbitrarily shaped domains. It also simplifies the contact geometric operations. But, their performance is known to be poor, for example, in the representation of bending of walls and pillars. Higher order elements, such as 20-node bricks, provide a good performance with only one element across the thickness, but they render contact calculations more time-consuming. Contact representation, either with rigid or deformable blocks, to achieve good bending behavior is addressed in the next section.
2.3. Contact Between Blocks
Most discrete element models adopt a simplified representation of the contact between blocks based on sets of point contacts. Therefore, no joint or interface elements are defined, contrary to finite element micro-models. The main justification of the simplified contact representation is that, for systems composed of blocks of geo-materials, the joints may be irregular or ill-defined, and it is not possible to seek accurate stress distributions along the discontinuities. Furthermore, for irregular masonry patterns, or for relatively loose systems, blocks often interact through edges or points and not along surfaces. The point contact approach is more versatile and facilitates the analysis in the large displacement range, as the system connectivity changes, and the type, location and orientation of contacts has to be periodically updated. The drawback is that more contact points are required to achieve a given accuracy of contact stresses.
The point contact approach assumes that the stress at a contact point is a function of the relative displacement of the 2 blocks at that point. Contact forces are calculated by assigning an area to each point. For rigid blocks, the discrete contact points are placed at locations of vertex-face or edge-edge interaction. For deformable blocks, additional contact points are created for the nodal points of the internal FE mesh that fall on block boundaries.
For example, in the 3DEC code [3], for contact purposes, the faces of polyhedral blocks, whether assumed rigid or deformable, are discretizes into triangular sub-faces. There are 2 types of elementary or point contacts: vertex-to-face (VF) and edge-to-edge (EE). A contact point of VF type is placed at every location where a vertex touches a face,whilea contact of EE type is created where 2 edges meet. Vertex-to-edge or vertex-to-vertex contacts are considered particular cases of the VF type. A face-to-face or edge-to-face interaction is represented by several elementary contacts. The contact stiffness is dependent on the contact area, so, even when the point contact assumption is employed, it is useful to assign areas to the elementary contacts. For a face-to-face interaction, the sum of the elementary contact areas should equal the real contact area. For the true edge or point contacts, a minimum stiffness needs to be assumed, so codes have rules to set minimum areas, depending on the system geometry and scale, or allow users to define.
The analysis of pillars or walls requires an accurate representation of the bending behavior. When deformable blocks are employed, the internal FE mesh needs to be fine enough to capture the linear stress diagram; for example, if triangles or tetrahedral are used, then 4 elements across the thickness are advisable. When rigid blocks are used, the bending deformation is concentrated at the joint. It is possible to refine the contact discretization, to match the analytical bending performance. To illustrate this option, Fig. (1a) shows 2 brick-shaped rigid blocks. Typically, in codes such as 3DEC, a rectangular face is divided into 2 triangles (Fig. 1b), resulting in contact points at the 4 vertices. In this case, if a moment is applied to the top block, the bending response is too stiff, and the deflection will be lower than the analytical solution. However, if the face discretization is refined (Fig. 1c), 9 contacts points can be generated, leading to an improved performance is bending, even if each block is still a rigid body. The way contact areas (or weights) are calculated depends on the formulation used in each DEM code, but they can actually be chosen to reproduce the bending deflections of the elementary theory. For dynamic analysis, this issue is tied with the natural frequency calculations for slender components, to be addressed in the next section.
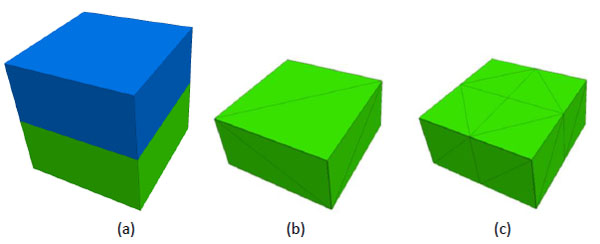
Model with 2 rigid blocks (a); 2 face discretizations for contact calculations (b, c).
3. ANALYSIS OF DYNAMIC BEHAVIOR
3.1. Dynamics of Masonry Structures
Masonry structures display a strongly non-elastic behavior from low load levels, which is understandable given the low or null tensile strength of masonry joints. Under cyclic loads, the radical different behavior of joints under tension and compression leads to a complex response. Nevertheless, the assumption of linearity always provides auseful frame of reference, and a good way to check the model for input errors, as linear response is easier to predict. Before undertaking a non-linear analysis, it is helpful to run an elastic model, to try to understand the global response under dynamic loads, governed by the interplay of the various structural components, their deformability, and the way they are connected. In fact, ambient vibration tests provide an estimate of natural frequencies and mode shapes that characterize the structure’s dynamics under very low intensity excitation, which cannot trigger significant changes in the structure and non-elastic phenomena.
When rigid block models are used, the global deformability of the structure in the elastic is totally governed by the joint stiffness parameters, the normal stiffness, and the shear stiffness. These must be chosen to provide the complete deformation of the structure, from the units and the joints. Calibration of the joint stiffness parameters to match the measured frequencies and mode shapes is a good starting point in seismic studies.
For deformable block models, the compliance of units and joints must be specified separately. Again, experimental calibration is advisable. It may be difficult to be rigorous in attributing the relative contribution of units and joints, but the sum of the sources of elastic deformation must match the global structural flexibility. Typically, it is not necessaryto use very stiff joints. When the joint stiffness is high enough so that joints areonly responsible for a small fraction of the globaldeformation, then its effect on the resultsis generally reduced. There is no need to increase it further (and it is also not numerically advisable). Joint strength properties, friction and tensile or shear bonds, are the key parameter in safety assessment studies.
3.2. Natural Frequencies
Performing an eigenvalue analysis of the structure is always useful, as long as it is understood that under intense earthquakes the nature of the response will change, particularly if damage takes place. If experimental data on identified frequencies are available, they are very useful in the calibration of the deformability of the numerical model. For historical structures, given the diversity and variability of materials, these tests provide an integrated picture of the global response which is quite valuable.
For deformable blocks, eigenvalue calculations follow the standard FE practice. For rigid block models, it is also possible to perform these analyses, by assuming that contacts are elastic and the response is linear. Each rigid block has 6 degrees of freedom in 3D, and 3 in 2D, and using these variables a stiffness matrix of the block system can be formed by assembling the contributions of the normal and shear stiffness of each point contact. A diagonal mass matrix can also be obtained from the mass and the moments of inertia of each block.
Comparisons of the natural frequencies of rigid block systems with analytical solutions for elastic beams or plates have shown that the approximation is sufficient for practical purposes [4]. To represent bending of pillars or walls correctly, at least 3 contact points across the thickness should be used, as discussed in the previous section. The case of an elastic cantilever wall with three sections of different thickness Fig. (2) was studied by [5], who developed a numerical solution of the vibration modes, based on the Mindlin plate theory. Table 1 compares this solution with the results of a FE model (with a 20-node brick element mesh) and a rigid block model (created with the code 3DEC). It can be seen that the continuum FE model has a better performance, but the rigid block representation provides a quite reasonable approximation. The four mode shapes of the rigid block model are shown in Fig. (2) [4].
Natural frequencies (Hz) of the stepped cantilever wall problem.
| Mode | Mindlin plate theory [11] | FE model | Rigid blocks |
|---|---|---|---|
| 1 | 1.40 | 1.40 | 1.36 |
| 2 | 2.52 | 2.50 | 2.99 |
| 3 | 5.46 | 5.37 | 5.48 |
| 4 | 6.18 | 6.10 | 6.68 |
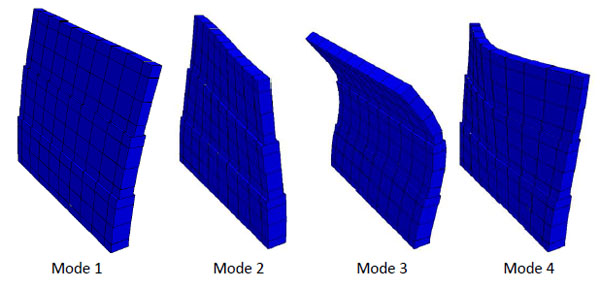
Stepped cantilever wall problem. Mode shapes obtained with a rigid block model.
3.3. Dynamic Analysis Procedures
DEM codes typically use explicit algorithms to obtain solutions, either for static calculations (using the dynamic relaxation concept) or for time domain dynamic analysis. The simplicity and generality of these methods are attractive, particularly for problems in which it is necessary to take into account changes in the system geometry and connectivity as deformation and failure process develop.
The serious drawback of an explicit algorithm is the need to limit the time step to guarantee numerical stability. In practice, time steps become dependent on the stiffness of the various system components: it is the thinnest continuum element, or the rigid block with the larger ratio of stiffness/mass, which govern the time step. This has important implications in the idealization of the structure. A system comprising both very stiff and very flexible elements leads to a time consuming analysis. Therefore, deformable blocks with very stiff material are to be avoided: it is better to represent them as rigid blocks, assigning all the system deformability to the joints. The use of very stiff joints, with stiffness viewed as a penalty coefficient to limit interpenetration, is also not recommendable.
Rayleigh damping is commonly used in time domain analysis. It should be noted that the stiffness component will require a further reduction the stable time step. In block models, energy dissipation also occurs by frictional slip on the joints, so the selection of the amount of viscous damping has to take this into consideration, to avoid unconservative results.
4. REVIEW OF STRUCTURAL MODELING CASES
4.1. Block Rocking
Analysis of the dynamic of a free-standing column or wall is often performed by representing it as a single rigid block, using well-known analytical solutions, such as Housner’s. Discrete element models are capable of reproducing the analytical results, and allow more general shapes and seismic records to be used. [6] compared shaking table tests of single blocks under harmonic and seismic records with the analytical solutions and DEM rigid block models, demonstrating the capability of the numerical models to address this problem. Fig. (3) shows a comparison of DEM with an experiment andan analytical solution.
The good match was obtained by matching the DEM model parameters, contact stiffness and damping constant, with the test results. The analytical solution was based on the concept of restitution coefficient, which had also to be calibrated. This example shows that the spring-dashpot contact model can approach both the classical solutions and the experimental evidence, but a calibration procedure is required, as discussed by [6].
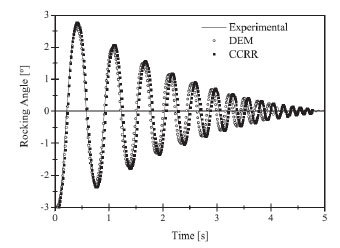
Free rocking response of block. Comparison of experiment, DEM and analytical solution (CCRR) (from Pena et al. 2007).
More generally, these and other similar studies highlight the variability and sensitivity of the rocking problem to the geometrical and mechanical properties and to the dynamic input, which is also clearly noticeable in experiments. It shows the importance of performing multiple analyses and parametric studies, considering the expected bounds of the less well known data, when the safety under dynamic loads is to be assessed.
4.2. Columns and Tall Structures
The behavior of drum columns under dynamic excitation has been addressed by several authors in the context of studies of the classical architectural heritage. [7] analyzed the collapse of single columns, using 2D rigid block models, under different dynamic excitations. [8] simulated numerically the Parthenon columns and column-architrave sub-structures with 3DEC. Rigid block models were used, with polyhedral blocks that in some cases reproduced the existing irregularities and damage of the drums (Fig. 4). The results made evident the detrimental effect that damage can have on the safety of the structure.
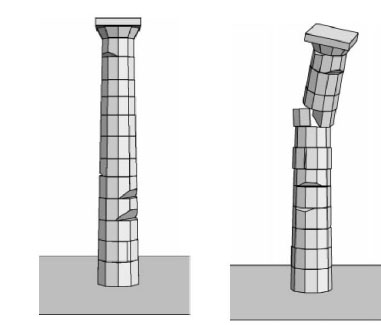
Models of drum columns with existing damage (Psycharis et al., 2003).
Another type of tall structure approached with discrete elements is the case of historical masonry minarets (Fig. 5) [9]. Again rigid blocks were employed, but it was necessary to insert structural elements,with non-linear behavior, to simulate the metal connections between the stones in each circular ring. Joint stiffnesses were calibrated using the natural frequencies obtained in ambient vibration tests.
Masonry spires are also very vulnerable to seismic events. [10] analyzed one of these structures with a rigid block model, considering the effect of dynamic pulses on the development of progressive collapse.
The importance of rocking phenomena for the stability of this type of tall structures make clear the significance of shaking table experiments, as discussed in the previous section, to validate the DEM performance.The use of a sufficient number of contact points is also important, as already pointed out in section 2.3.
The calibration of the global deformability is crucial to obtain a realistic response. When ambient vibration tests are available, the joint stiffnesses can be directly calibrated, eliminating the uncertainty typically involved in the assignment of joint properties. As shown in section 3.2, a rigid block model can reproduce fairly well the response of a column or plate in the elastic range. This is essential to ensure that the correct failure mechanisms may develop during the simulation.
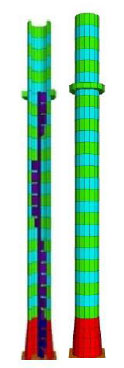
Model of a minaret (Catki et al. 2014).
The use of deformable blocks can provide useful insight into the stress patterns inside the blocks, as shown by [11] for a column-architrave system. A fine mesh used inside the blocks allowed the stress paths to be identified, showing the interaction of the various structural components. However, explicit dynamic analysis for such a model would be quite time consuming, due to the time step restrictions already mentioned. These authors opted for static equivalent loads to represent the seismic action. For dynamic analysis, a rigid block representation would be advisable.Such a model could be verified and calibrated by comparison with the refined model in pushover tests.
4.3. Masonry Walls
Observed damage in earthquakes has shown the vulnerability of masonry walls to out-of-plane bending. [12] has analyzed the out-of-plane collapse mechanismsof masonry walls with complex cross-sections, e.g. 2-leaf walls (Fig. 5), comparing push-over methods and dynamic analysis. The figures illustrate very well the capability of DEM to simulate irregular blocks shapes and complex arrangements that replicate the patterns observed in traditional masonry constructions.
Push-over analysis often provides a useful insight into the problem, at least to view the possible failure modes, and it is much less demanding in computational terms than a full dynamic analysis. The latter were performed by [13] to study the behavior of the Parthenon walls with a rigid block model with frictional joints (Fig. 6). In particular, the effects of different seismic motions were examined.
The capability of DEM models to replicate complex block geometries and arrangements is well illustrated by the examples in Figs. (6, 7). Pushover analyses can be readily performed, even for large 3D models. However, time domain dynamic analysis maybe expensive, due to the time step restrictions, when small blocks are present. Simplification of the models, or a careful choice of physical parameters, may be necessary, as explained in section 3.3.
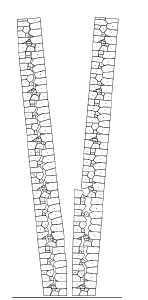
Analysis of failure modes of wall sections (De Felice, 2011).
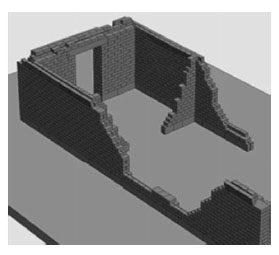
Model of the Parthenon walls (Psycharis et al. 2011).
4.4. Arches and Vaults
Arched and vaulted structures have been analyzed with discrete elements by many authors, for example, the case of arch bridges. Most of the analyses have considered static loads or statically equivalent seismic loads. [14] performed dynamic analysis of simple structures, such as free-standing circular or pointed arches, under seismic records. Block analyses of arches under impulsive base motions were presented by [15].
There is less experimental data to verify the numerical results for this type of structures, particularly for collapse conditions. Results from dynamic monitoring of bridges or domes may help to check the elastic response range, but further research is needed in terms of failure loads or assessment of permanent displacements.
4.5. Modeling Observed Displacements and Damage
The lessons learned from the performance of structures under recent earthquakes are extremely useful to understand their dynamic behavior, and provide a good validation exercise for numerical models that need to be capable of reproducing the observed failure modes. The aim is not to match closely the measured displacements, which would be a pointless exercise, but to reproduce the observed modes of deformation and the types of collapse modes. Sensitivity of the numerical representations to the various physical parameters, often of difficult determination, can also be assessed. For example, [16] applied discrete element models to interpret the observed effects of the Azores 1998 earthquake on various simple structures, such as statues or chimneys, which were displaced or damaged.
Numerical models are also being used as simulation tools to support other fields of knowledge. For example, [17] studied the effect of earthquakes on models of columns to infer historical PGA values, given the observed failure patterns. Models can also be useful in the context of archeological discussions about the events that led to the destruction of monuments or buildings, for example, to examine if an earthquake is a plausible cause [18].
The use of DEM models to interpret past seismic events is growing. Obviously, there is never enough data for the required simulations, the initial state of the structures is not always well known, and the seismic records are not available. So, some care is needed in the conclusions. But, often parametric studies can provide very useful bounds to the various types of behavior, and helpful insight and information can be gained.
CONCLUDING REMARKS
The ability of discrete element models to represent the essential features of the observed failure modes of masonry structures makes them an important tool in seismic analysis. There is not a rigid boundary between finite elements and discrete elements, as deformable block formulations and FE micro-modelling often overlap to some extent. The ability of a given code to replicate a complex geometry, and to perform a simulation in an efficient manner, is more important in practice than the underlying formulation.
Static push-over techniques can be easily implemented for simplified studies of safety assessment. However, it is in the context of time domain dynamic analysis that the models better display their potential as simulation tools. The computational effort required may still be significant, in the case of large 3D models. Pushover analysis can usually be made with large models involving deformable blocks for internal stress analysis. Dynamic runs tend to require rigid block idealizations and more simplified models.
Discrete elements have been mostly effective in the study of simple constructions and structural components, such as columns or walls, but are now increasingly being extended to more complex problems. The challenge to the practitioner is to simplify the modeling of the structures, discarding inconsequential details and concentrating on the key aspects that govern the response. Typically, block sizes larger than the real ones need to be employed, what requires a careful strategy to define the appropriate properties for the block material or the joints. It is essential to achieve an effective engineering representation to be employed in the parametric studies that are always advisable in masonry analysis.
Models for dynamic analysis always need to simulate correctly the nearly elastic response that occurs for lower level excitation. Otherwise, the collapse mechanisms and load may not be meaningful. Data from in situ dynamic characterization is always very helpful in model calibration.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
AKCNOWLEDGEMENTS
Decleared None.


