All published articles of this journal are available on ScienceDirect.
Rocking Behaviour of Multi-Block Columns Subjected to Pulse-Type Ground Motion Accelerations
Abstract
Ancient columns, made with a variety of materials such as marble, granite, stone or masonry are an important part of the European cultural heritage. In particular columns of ancient temples in Greece and Sicily which support only the architrave are characterized by small axial load values. This feature together with the slenderness typical of these structural members clearly highlights as the evaluation of the rocking behaviour is a key aspect of their safety assessment and maintenance. It has to be noted that the rocking response of rectangular cross-sectional columns modelled as monolithic rigid elements, has been widely investigated since the first theoretical study carried out by Housner (1963). However, the assumption of monolithic member, although being widely used and accepted for practical engineering applications, is not valid for more complex systems such as multi-block columns made of stacked stone blocks, with or without mortar beds. In these cases, in fact, a correct analysis of the system should consider rocking and sliding phenomena between the individual blocks of the structure. Due to the high non-linearity of the problem, the evaluation of the dynamic behaviour of multi-block columns has been mostly studied in the literature using a numerical approach such as the Discrete Element Method (DEM). This paper presents an introductory study about a proposed analytical-numerical approach for analysing the rocking behaviour of multi-block columns subjected to a sine-pulse type ground motion. Based on the approach proposed by Spanos et al. (2001) for a system made of two rigid blocks, the Eulero-Lagrange method to obtain the motion equations of the system is discussed and numerical applications are performed with case studies reported in the literature and with a real acceleration record. The rocking response of single block and multi-block columns is compared and considerations are made about the overturning conditions and on the effect of forcing function’s frequency.
1. INTRODUCTION
Ancient columns, made with a variety of materials such as marble, granite, stone or masonry are an important part of the European cultural heritage. In particular columns of ancient temples in Greece and Sicily which support only the architrave are characterized by small axial load values. This feature together with the slenderness typical of these structural members clearly highlights as the evaluation of the rocking behaviour is a key aspect of their safety assessment and maintenance [1, 2].
The rocking response of rigid blocks has been widely investigated in the literature in the last forty years. Housner (1963) [3] provided the general theoretical frame for studying the rocking behaviour of a rigid prismatic block. That seminal paper and the following research which considered different forcing laws[4-6], 3D behaviour [7-9], effect of the ground stiffness [10], dissipators [11] etc. showed that the dynamic behaviour of block-like systems is strongly non-linear and consequently quite difficult to be treated analytically. Most of this research focused on the response of single block structures.
A very limited number of authors investigated analytically the behaviour of stacked rigid block systems. The analysis of these types of structures is made complex due to the fact that the number of rocking patterns increase exponentially with the number of superimposed blocksand this affect the equations of motion governing the response of the system.
Because of these difficulties, the most common way to approach the problem is by means of numerical methods. For example, previous studies showed that the Distinct Element Method (DEM) [1, 12-14] seems to be an efficient tool in predicting the response satisfactorily. However, verification and calibration of the main parameters, especially the joint properties, is necessary, before such a numerical method can be used in the restoration process of a classical monument.
Among the few analytical studies Blasi and Spinelli [15] proposed an iterative procedure to study the rocking behaviour of stacked rigid block columns, including the mechanical behaviour of the interface. Spanoset al. [16] developed the equations of motion for a two-block system on a rigid foundation and considered the four possible patterns response under free and induced vibrations and the transition from one pattern to another. However this approach is not easily scalable to multi-block system. Kounadis et al. [17] analysed as well a two block system under ground motion and compared the stability of the system to that of an equivalent single block. A more efficient vector representation of the motion equation was given by Saitta et al. [18] who analysed a three and five block systems under free and forced vibration.
In this paper the approach used by Spanos et al. [16] is followed to show the unfeasibility for N-block systems with N>2. The initial conditions for the initiation of the motion are calculated and the different rocking patterns are studied. Finally, two numerical analyse of a two-block and three-block systems are carried out using Working Model 2D [19] with the aim to prepare for an analytical representation of the response. The numerical results of equivalent one-, two- or three-block systems are compared to the exact solution of one single block subjected to a pulse-type base excitation as studied by Zhang et Makris [4].
2. INITIATION OF MOTION
A system composed of N rigid superimposed blocks can be set into rocking motion if subjected to horizontal and vertical ground accelerations. In the following each rigid block has mass Mi, centroid moments of inertia IG, i, base and height respectively equal to 2bi and 2hi. Each block can rotate against its own right bottom point Oi and left bottom point O'i and the rotation angles are measured from the vertical in clockwise direction, see Fig. (1).
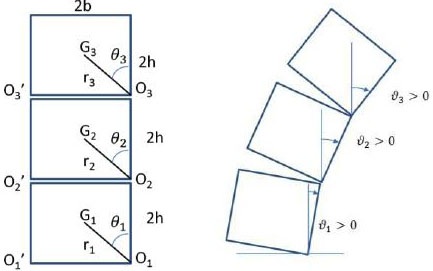
Initial conditions.
The system may be set into rocking under N couple of symmetrical initial condition patterns for a total of 2N initial conditions. The motion is initiated when, for a sub-system of blocks the overturning moment of the horizontal inertia force about one edge exceeds the restoring moment due to the weight of the sub-system and the vertical inertia force. The patterns are indicated in the following as Pi, a or Pi, b for a positive or negative initial rocking angle respectively. Each initial condition pattern can be described by the following inequality:
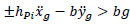 |
(1) |
where hp, iis the height of the centre of gravity of the sub-system with respect to the surface on which it rocks
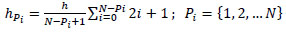 |
(2) |
In Eq. (2) i indicates the i-th block and Pi is a pattern in which N-i + 1 blocks rock together starting from the i-th block.
For a system composed of 3 identical blocks motion can be set under 6 initial condition patterns as shown in Fig. (2); for each of them the height of the centre of gravity of the system is as follows:
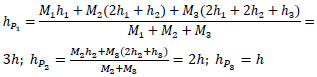 |
(3) |
In Table 1 the values of the height of the CG of the sub-system with respect to the surface on which it rocks are calculated for a system composed of one, two or three blocks. In Table 2 the minimum longitudinal acceleration for these systems with a global geometrical ratio α=0.25 are reported.
3. EQUATIONS OF MOTION
An analytical formulation of the rocking behaviour of a system of stacked blocks has been given by Spanos [16] for a system composed of 2 blocks having different mass and size. For a system of N superimposed blocks the equations of motion can be obtained by applying the Eulero-Lagrange method:
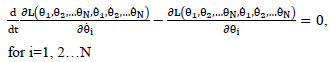 |
(4) |
where
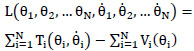 |
(5) |
and Ti and Vi are respectively the kinetic and the potential energy of the i-th block. Therefore the problem lies in determining the kinetic and the potential energy for each block and for each rocking mode of the column.
The kinetic and potential energy for each block can be written as
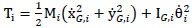 |
(6) |
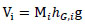 |
(7) |
where θi is the rocking angle of the i-th block with respect to the vertical, XG,i, XG,i are the coordinates of the centre of gravity of each block, and is the distance of the i-th center of mass from the base of the base block.
For a system of N blocks there are 3N possible block patterns, among which one is a stable configuration and (3N-1)/2 are independent rocking modes, see Fig. (3).
4. IMPLEMENTATION AND NUMERICAL ANALYSES
In the following a comparison between the normalised time history response θ(t)/ α of a system as composed of a single rigid block or a multi-block system is proposed, see Fig. (5). The elements of the multi-block systems are numbered from the base to the top as “Block I, II and III”. Each block has the same base width of the single block system and height equal to 1/2 or 1/3 of that of the single block system, see Fig. (4).
The solid block has frequency parameter p=2.14 rad/sec, geometrical ratio α=0.25 rad and restitution coefficient xC ν=0.9. The dynamic features of the column are the same of the case examined in [4], whose analytical solution is also reported in red. Each system is subjected to a sine pulse having Ω/p=5 and to four different amplitudes, 3α g, 3.01α g, 6.32α g and 6.33α g.
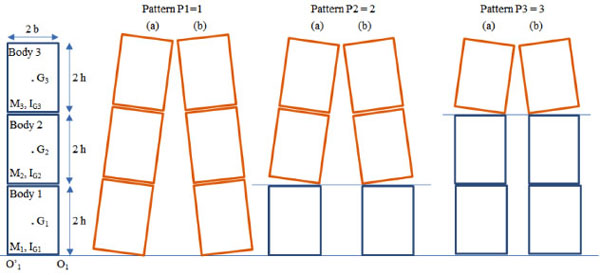
Initial conditions.
Geometrical data.
| System | hp, i | |||
|---|---|---|---|---|
| Pattern 1 | Pattern 2 | Pattern 3 | ||
| 1 block | hblock= Hsystem | hpi = h | / | / |
| 2 block | hblock = 1/2Hsystem | hpi 2 = h | h p2 = 2 | / |
| 3 blocks | hblock = 1/3Hsystem | hpi 3 = h | hp2 = 2 h | hp3 = h |
Geometrical and acceleration data.
| System | H (system) (m) |
h (block) (m) |
b (block) (m) |
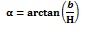
|
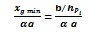
|
||
|---|---|---|---|---|---|---|---|
| Pattern 1 | Pattern 2 | Pattern 3 | |||||
| 1 block | 1.56 | 1.56 | 0.4 | 0.25 | 1.02 | / | / |
| 2 blocks | 1.56 | 0.78 | 0.4 | 0.25 | 1.02 | 2.04 | / |
| 3 blocks | 1.56 | 0.52 | 0.4 | 0.25 | 1.02 | 1.53 | 3.06 |
For these geometrical characteristics the one block system will be overturned for a sine amplitude pulse in the interval [3.01αg, 6.32αg] but will rock without being overturned for pulse amplitude in the range [6.33αg, 7.17αg].
The numerical normalised time history responses of the multi-block system have been obtained using Working Model 2D a software widely validated in the literature which computes the motion of mechanically interacting rigid bodies under several constraints and actions of forces, displacements or accelerations, including the treatment of interfaces. In Working Model 2D, the satisfaction of all imposed constraints at the contact interfaces is enforced simultaneously during the numerical integration by means of static and kinetic Coulomb friction.
The numerical integration of the motion equations together with the satisfaction of the constraint conditions (friction and restitution), is done using the Kutta-Merson method (5th order Runge-Kutta).
With this variable time step integration scheme, near collision, the time step is reduced appropriately to restrict the overlap between bodies from exceeding the specified overlap tolerance. For all the numerical analysis carried out in the present work, the overlap error tolerance was set to 10−5 cm.
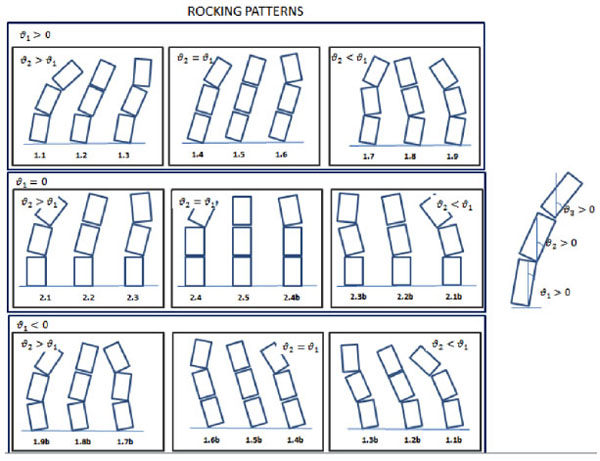
(a) Reference system; (b) Rocking modes.
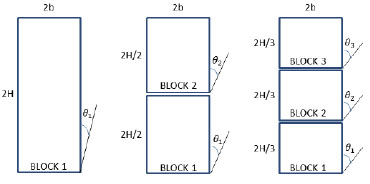
Analysed systems.
Preliminary to the analysis a detailed calibration of the model was made by comparing the numerically obtained response and the analytical solution provided in [4]. The size and the mass of the solid block were changed until the numerical solution fits the analytical curve, keeping the frequency parameter and the restitution coefficient constant. The ground acceleration was simulated by imposing the required forcing function to the centre of gravity of a rectangular rigid body with zero mass, in order to avoid any additional inertial effects. Static and kinetic friction coefficients were assumed equal to 0.8 and 0.5 respectively. These values proved to be suitable to avoid sliding between the blocks and between the column and the ground.
From each case analysed it clearly emerges as the numerical solution matches closely the one reported in Zhang and Makris [4], highlighting as the procedure can be considered correct.
The comparison between the behaviour of the solid block and the multi-block columns highlights as the single body system is more vulnerable to the overturning risk. The single and the two body systems behave in similar manner, while the three-block assembly has a strongly different response with lower oscillation amplitudes. Furthermore, it is evident as for low peak acceleration values Fig. (5a, b) the behaviour of the each block of the multi-body system is approximately identical and consequently their rocking motion is dominated by pattern 1.5 (Fig. 3). When the peak acceleration increases Fig. (5c, d) the behaviour of the three-block column changes and the lower body experiences smaller oscillations until remaining in its equilibrium position, while the upper blocks continue oscillating with similar rotations (pattern 2.2 Fig. 3). In each case examined, the three-block column does not overturn. Although these results seem to show that multi-block systems could be more safe than monolithic members, it has to be reminded that the above mentioned results are valid for the adopted frequency range of forcing functions (Ω/p=5).
Fig. (6) shows the time history analysis of the above mentioned systems subjected to the real ground acceleration record of the Friuli (1976) earthquake (PGA=0.48g, Fig. 6a). In particular, only the response of block I and block II are reported respectively for the two-block and the three-block systems for the sake of clarity. The results show that the solid column and the two-body system tend to recover their xC initial position after experiencing large oscillations, while the three-block system overturns suddenly. The overturning mechanism is related to the two top blocks while the base body tends to be stable. This fact is due to the different frequency content of the real accelerogram adopted. Further studies will be addressed to investigate on the dependence of the overturning conditions from the frequency of the adopted sine pulse.
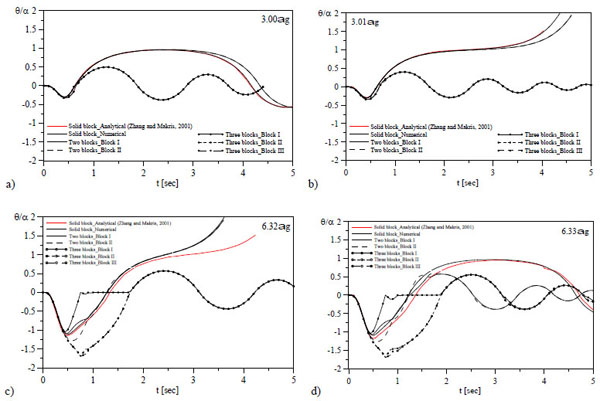
Normalised time histories of solid, two and three block systems subjected to a sine pulse (Ω/p=5). (a) ag=3αg; (b) ag=3.01αg; (c) ag=6.32αg; (d) ag=6.33αg.
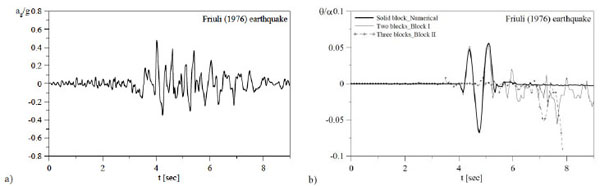
Time history response to the Friuli (1976) earthquake. (a) Adopted acceleration record; (b) Time history analysis.
5. REMARKS
The case study presented in the previous section shows that it is not possible to model the rocking response of a system composed of N superimposed blocks as a single rigid system. In fact although this simplification might be conservative for a single pulse ground acceleration the simulations carried out for a more complex ground time history lead to completely different results. This example shows that analytical solution of multi-block systems s might be necessary for investigating the safety domain of such systems. However, the analytical formulation by Spanos et al. [16] may be feasible only for system with an extremely limited number of sub-blocks.
The numerical intractability of the problem arises from the fact that the CG coordinates, their derivatives and the height of the CG over the base of the base block depend on the pivot around which the blocks rock and on the pivot coordinates of all the blocks below. This implies that for a system of 3 blocks 6 different system of equation needs to be written for the CG of the blocks according to the sign of the rocking angle, each one depending on possible pivot configurations, for
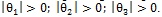
Although straightforward, this method it’s not easy to generalise to an arbitrary number of elements as it involves an exponentially growing number of sub-cases. Therefore, a different kind of parameterisation must be used. A promising approach could entail expressing the potential energy of the system of N blocks recursively starting from the potential energy of N-1 block system. We are currently considering several parameterizations which have this property.
CONCLUSION
This paper presented an introductory study on the rocking behaviour of multiple block systems. The problem was approached with an analytical approach based on the energetic Eulero-Lagrange method and a case study was implemented using Working Model 2D.
From the analytical formulation it emerges that despite the method providing a direct physical insight of the problem it can be implemented only for a system with no more than 3 sub-blocks.
The case study has shown that multi-block systems for the range of examined parameters are less sensitive to overturning risk with respect to the monolithic member with the same geometrical dimensions and that overturning conditions depend on the frequency of the external input;
More work will be addressed to validate the implemented algorithm with Discrete Element Method analyses and to study the effect of frequency content on the overturning conditions of multi-block columns.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTs
Declared none.


