All published articles of this journal are available on ScienceDirect.
Impulsive Tests on Historical Structures: The Dome of Teatro Massimo in Palermo
Abstract
Cultural heritage is the set of things, that having particular historical cultural and aesthetic are of public interest and constitute the wealth and civilization of a place and its people. Sharpen up methodologies aimed at safeguarding of monuments is crucial because the future may have in mind the historical past. Italy is a country that has invested heavily on its historical memory returned in large part by the historical building or the monuments. Furthermore, culture represents a fundamental indicator of the growth of the culture of a country. Consider a monitoring project of one of the most Impressive theater in the world, like “Teatro Massimo” in Palermo (Italy), means to add value to both of the issues mentioned above. Among several methods providing useful information about the conservation status of the structures, dynamic monitoring techniques are suitable to check and restore the global behavior of the buildings. The anomalous features diagnosis of the structural dynamic response is an index of alterations of the material state and, in the worst cases, is related to the presence of damaged structural elements. The present paper assesses, through a real investigation, the importance of dynamic tests on historical buildings. In particular impulsive tests return the main structural characteristics describing the current behaviour. Such tests are then crucial for updating numerical evaluation and check the need of restoring original main features or not, suggesting a strategy of restoration as well.
1. INTRODUCTION
An international competition for the creation of the opera house was announced by the Palermo Council in 1864 at the instigation of the mayor, Antonio Starrabba Rudinì. Giovan Battista FilippoBasile won this competition, he was well known in Sicily for his previous cathedral restoration design in the city of Acireale, as well as garden designs in the city of Palermo and Caltagirone. The opera house was designed and overseen by himself and after his death in 1891, construction was then overseen by his son, Architect Ernesto Basile. Construction started on 12 January 1874, but was stopped for eight years from 1882 until 1890. Finally, on 16 May 1897, twenty-two years after the laying of the foundation stone, the “Teatro Massimo” in Palermo, Fig. (1a) the third largest opera house - after the PalaisGarnier in Paris and the K. K. Hof - Opernhaus in Vienna - was inaugurated with a performance of Verdi's Falstaff conducted by Leopoldo Mugnone [1]. Very impressive is the circular dome whose cover is made of copper sheet, 2 mm thick, rivetted to a wooden plank whose weight is transmitted to the steel arches by means of wood purlins [2]. At the top of the dome there is a wonderful fleuron in bronze with iron frame, 7 m high and weighting 9600 kg (Fig. 1b).
The real peculiarity of this dome is to be the contemporary in 1876. In fact it lays on sliding support and this ingenious arrangement makes the structure behave not redundant, allowing the displacements induced by temperature variations without increasing stress state. However, since, today the supports appear to be completely blocked, because of the advanced oxidation (Fig. 9), then a dynamic test will return the real behaviour of the structure leading to identify the characteristic parameters necessary to perform a numerical analysis to evaluate the increments of the stress in this present condition.

View of Teatro Massimo in Palermo: (a) aerial view; (b) view of the fleuron in bronze.
2. THE STRUCTURE OF THE DOME
The iron dome of the playhouse is projected in a circle 28.73 m in diameter, covering the audience hall, the space occupied by the loggias. Laying over rollers, for temperature variations, it is composed of sixteen radial arches, five polygonal rings, and one hundred twenty-eight diagonal braces that intersect each, as shown in (Fig. 2).
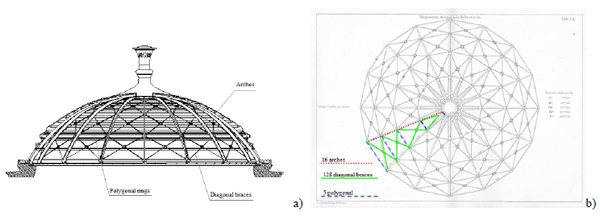
Elements of the iron dome: (a) front projection; (b) horizontal projection (from the original Basile’s drawings Table VII).
Each upper boundary of the arch is a cubic parabola with vertex m high. 8.22 with respect to the horizontal plane passing through the point where the arch bends vertically, (Fig. 3).
Fig. (4) reproduces the view of the dome as it appears to an observer in the room below the roof and accessible from the fourth balcony of the Teatro Massimo. From this image it is possible to detect the shape of the arches, the arrangement of the braces, wood purlins and plank.
Moreover, the arch is divided into four pieces of variable double T section, the first 152x193mm, 152x243mm the second, the third and finally the fourth 152x295mm 152x390mm Fig. (5), connected to each other in the joints with 12mm thick plates and nails of diameter 15mm. The purlins connecting the arches are made of poplar wood, with section 250x250 mm, connected by angle brackets 78x78x13 mm bolted with screws 18 mm in diameter.
The radial intermediate rings are composed of L profile of size 80x80x14 mm. The upper ring is composed of a flat sheet of size 181x13 mm and an angle of 75x75x13 mm. The lower ring is composed of a profiled plate 250x20 mm. Such rings, whose dimensions are reported in Fig. (6), are connected to the arches through three wings bolted plates with screws of 33 mm diameter. At plates are also bolted diagonal braces of steel round section diameter of 40 mm. As apparent from Fig. (7), these braces are provided of threaded end so as to screw them in a ring of 312 mm diameter in order to perform the stretching of the same rods as well.
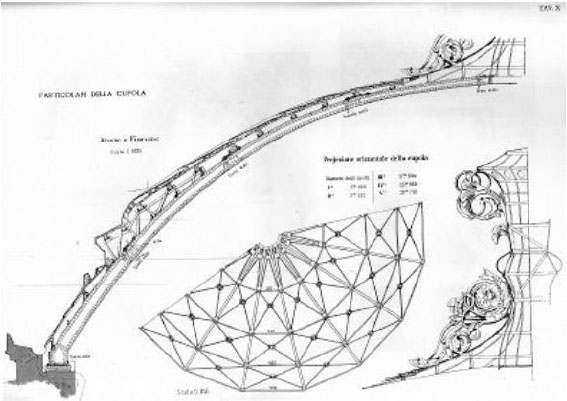
Details of the cover, of the planimetric arrangement of the braces and of the crowning fleuron, (from the original Basile’s drawings Table X).

Image of the view from inside the dome.

Dome structural details: (a) segmentation scheme of the arch; (b) transversal section.
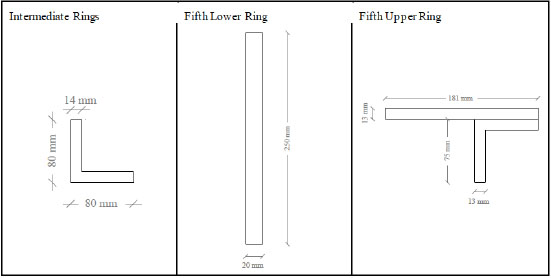
Transversal section of rings.

Details of braces.
It is worth stressing that in the original design of the structure, the arches rested on five steel rollers perfectly cylindrical and smooth surface with a diameter of 90 mm. The system of the rollers was contained in a iron box. Fig. (8) shows the sections of these support devices. This boundary condition was thought from Basile, to allow displacement of the base of the arches in the radial direction due to changes in temperature or of the vertical loads.
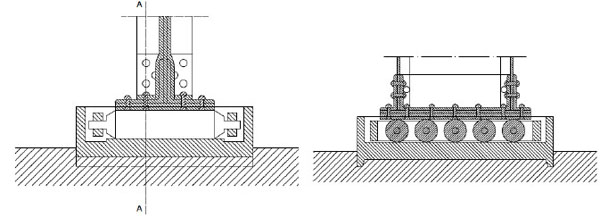
Sections of the support devices (from original drawings).
However, since, today the supports appear to be completely blocked, because of the advanced oxidation (Fig. 9), then it needs a dynamic test to capture the current structural behaviour useful for performing a numerical analysis to characterize the increments of the stress in this present condition.

Current condition of supports.
3. THE DYNAMIC TESTS ON THE DOME
The quantification of the increase of the stresses due to the prevented thermal expansion could be effected only through the finite element model analysis calibrated on the results of experimental tests. Then, it was necessary to plan and carry out dynamic impulsive tests detailed in the following.
3.1. Test Procedure
In order to perform the impulsive type tests, a steel wire rope has been passed around the arch in correspondence of the highest point of the dome and was bound to the floor using as a contrast one of the large steel beams that support the floor itself. Between the rope and the system of contrast were placed a hydraulic jack ENERPAC BRC 46, and a sleeve calibrated failure (Fig. 10). To simulate the impulsive load, the rope was stretched by means of the hydraulic jack. Increasing the pull on the rope, when the expected value of sleeve failure has been reached, the sudden breaking of the sleeve itself forces the structure of the dome to an impulse load at the point in which the steel rope was tied to the arch.

Test set up: (a) setup for the test pulse; (b) detail of the sleeve calibrated failure.
Further, to detect information on the behavior of the structure to different impulse intensities two series of sleeve were realized and calibrated to break for a tensile stress of 500 kgf and 1000 kgf, respectively. Three tests were performed with impulse 500 kgf sleeve and four tests with impulse 1000 kgf sleeve.
3.2. Experimental Set-Up and Data Acquisition
Once the structure has been forced by an impulse load it experiences vibrations. To record structural vibrations in terms of acceleration responses two different types of piezoelectric accelerometers have been used, manufactured by Bruel & Kjær and illustrated in Fig. (11), with high sensitivity, wide frequency range, small size, low weight, and easy installation, and whose characteristics are reported in (Table 1).

Accelerometers used; (a) Bruel & Kjær - Type 4382; (b) Bruel & Kjær - Type 4507-002.
Sensor features.
| Feature | B&K 4382 | B&K 4507-B-002 |
|---|---|---|
| Sensitivity: | 31 pC/g | 1000 mV/g |
| Measuring range | ±20 g | ±7 g |
| Frequency range | 0.10 ÷ 8400 | 0.40 ÷ 6000 Hz |
| Mass | 17 grams | 5 grams |
Piezoelectric accelerometers rely on the piezoelectric effect of quartz or ceramic crystals to generate an electrical output that is proportional to applied acceleration. The piezoelectric effect produces an opposed accumulation of charged particles on the crystal. This charge is proportional to applied force or stress. Therefore, when the system on which it is mounted the sensor exhibits an acceleration, the piezoelectric element within the accelerometer returns an electric charge proportional to the acceleration itself.
The electrical signal generated by the accelerometer is amplified and conditioned before being converted into a digital signal and recorded by an analog to digital card NI PCI-4472 manufactured by National Instruments with 8 analog input channels for simultaneous sampling with a resolution of 24 bits. The signals are processed in real-time applications with Labview specially designed for these tests.
The whole experimental equipment was provided by the Dynamic Laboratory of DICAM of University of Palermo.
3.3. Instrumentation of the Dome
As aforementioned, the structure of the dome is composed of sixteen arches radial symmetry. Because of this symmetry it is chosen to instrument a single pair of diametrically opposed arches, since the tangential displacements can be considered negligible, as confirmed by preliminary results obtained from a model of finite elements calculation (introduced in the next section).
In particular, seven accelerometers, numbered from zero to six, (as reported in Fig. (12)), in which an arrow indicates the positive direction), were screwed on a special plate of plastic material bonded on the surface of the intrados of the arch. In this regard it is important to emphasize that given the majesty and the configuration of the structure of the dome, place the accelerometer was not a simple task, but we have used the assistance of a professional rock climber Giuseppe Di Benedetto see Fig. (13) that here we thank firmly. For each test structural response was acquired by all sensors for a period of at least 120 seconds from the start of the impulse test with a sampling frequency of 1000 points per second.
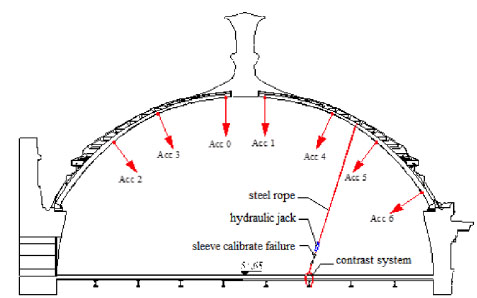
Schematic arrangement of the accelerometers.

Instrumentation of the dome with the help of a rock climber.
Each accelerometer is connected to a charge amplifier, conditioner (PCB 481A01). Then all signals are converted into a digital signal and recorded by means of the software LABVIEW through the analog to digital card NI PCI-4472. A block diagram of the experimental arrangement is shown in Fig. (14). The signals are processed in real-time applications with Labview specially designed for these tests.
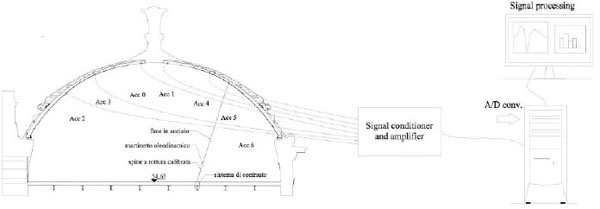
Block diagram of the experimental arrangement.
4. RESULTS OF THE EXPERIMENTAL TESTS IN TIME AND FREQUENCY DOMAIN
The dynamic characteristics obtained by the analyses of all signals are very close, then, for saving space, only results pertaining the impulse test of 500 kgf will be reported in this section.
Fig. (15a) shows the time histories of the recorded signals in terms of acceleration. Fig. (15b) represents the analysis in frequency domain through a Fourier transform of the recorded signals.
From Fig. (15b) it is apparent that the peaks of all the signals can be grouped into five frequency clusters as shown in (Fig. 16).
However, for the purposes of this investigation, in the following we will make explicit reference to the frequencies of the first cluster, in which four peaks are well distinguishable, at frequencies 3.71 Hz, 4.25 Hz, 4:46 Hz and 4.74 Hz, respectively.
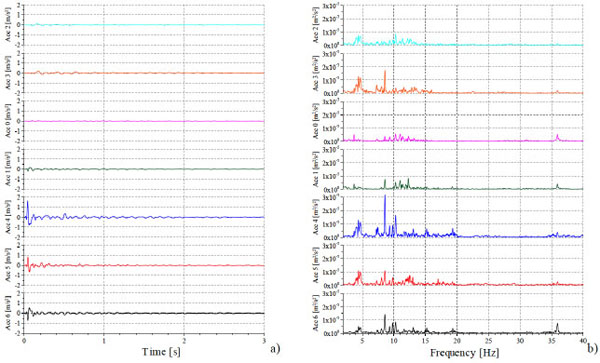
Recorded signals: (a) time domain; (b) frequency domain.

Five frequency clusters.
The accelerations recorded during impulsive test have been used for the evaluation of the first modal shapes, as prescribed by the well established output only identification procedure reported in [3-6]. The main steps are outlined in the following:
- Evaluate for each channel the average Fourier transform Gyjyj (ω) by using the FFT algorithm, where yj is the j-th measure location.
- Identify the natural frequencies ωi from the peaks in Fourier spectra.
- In Fig. (17) the FFT have been reported in terms of magnitude and phase for the first cluster of frequencies (letters from a) to d)).
- Use one of the measure location channels, say “Acc2”, as a pseudo-input.
- Compute the averaged frequency response functions (FRFs) between all other channels and the pseudo-input.
- At the i-th natural frequencyωi, the modal displacement amplitude of the j-th measure location is:
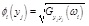
- Evaluate the sign of the modal displacements through the phase of the FRFs. In fact, it is well known that, in correspondence of a natural frequency, the phase angle of a FRF can be only equal to 0° or 180°. In the first case, the modal displacement of the j-th measure location has the same sign of the modal displacement of the reference point (“Acc2”), otherwise it has the opposite sign.
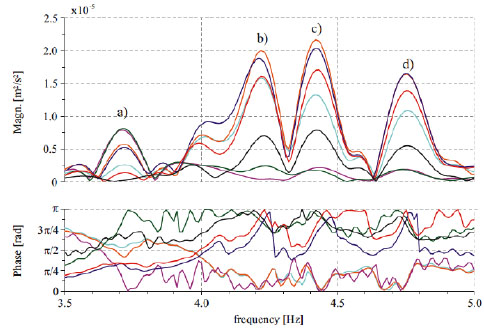
Magnitude and phase.
For the present case, in Table 2 the modal displacements, normalized with respect to the unity, have been reported for the first cluster of natural frequencies, while in Fig. (18) the correspondent modal shape have been depicted.
Modal displacements for the first cluster of frequencies.
| peak | a) | b) | c) | d) | |
|---|---|---|---|---|---|
| frequency [Hz] | 3.71 | 4.25 | 4.46 | 4.74 | |
| Channel | 2 | -0.287 | -0.444 | -0.394 | -0.401 |
| 3 | -0.428 | -0.498 | -0.506 | -0.496 | |
| 0 | -0.503 | -0.078 | -0.167 | -0.170 | |
| 1 | 0.511 | 0.179 | 0.139 | 0.170 | |
| 4 | 0.410 | 0.471 | 0.491 | 0.497 | |
| 5 | 0.210 | 0.450 | 0.456 | 0.454 | |
| 6 | 0.089 | 0.302 | 0.306 | 0.285 | |
5. THE FINITE ELEMENT MODEL
The aim of this section is to describe the Finite Element (FE) model of the dome realized by using SAP2000® v.10, a widespread, user friendly and well known package for structural analysis.
The structure of the dome has been modeled by using 736 1-D “frame” elements, 336 “joint” elements and it has 1750 degrees of freedom, and a perspective view of the Finite Element model of the dome is reported in Fig. (19).
The elements belonging to braces, purlins and polygonal rings have been modeled as pinned beams, due to the limited flexural stiffness of their cross sections.

Modal shapes for the first cluster of frequencies: (a) first modal shape; (b) second modal shape; (c) third modal shape.
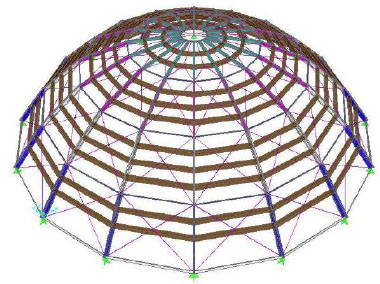
Finite element model of the dome.
Since mechanical properties of the materials actually present in the structure of the dome are not available, only for structural modeling purposes, the mechanical characteristics reported in Table 3 have been used for the first attempt model.
Materials mechanical properties.
| Steel | Wood | |
|---|---|---|
| Young’s modulus (MPa) | 210000 | 6500 |
| Poisson ratio | 0.3 | 0.3 |
| Shear modulus (N/mm2) | 807.7 | 2450 |
| Density (kg/m3) | 7850 | 600 |
| Coefficient of thermal expansion (°C-1) | 1,70·10-5 | 6,00·10-6 |
| Maximum allowable stress (N/mm2) | 100 | 20 |
The supports at the base of main arches of the dome, originally intended to allow small horizontal displacements (slides), have been modeled as fixed constraints. In order to assess how much the stress distribution in the whole structure depends on the kind of support at the base, some modal analysis on the FE model of the dome has been performed with different kinds of base support and, for each condition, the natural frequencies have been derived.
Results of the numerical analyses show that the first natural frequency is not so much affected by the base support constraints, but the higher modes frequency strongly depends on the base supports themselves. Natural frequencies along with participant mass ratio are reported in Table 4, in the condition of fixed base, while Fig. (20) reports two significant modal shapes.
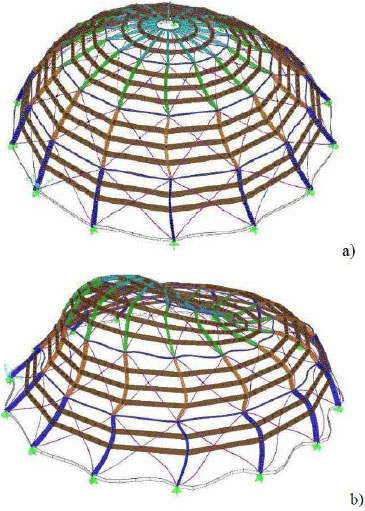
Modal shapes of the dome: (a) second modal shape; (b) seventh modal shape.
Significant natural frequencies of the dome (fixed base).
| N | Period | Frequency | Participant mass ratio | ||
|---|---|---|---|---|---|
| s | Hz | X dir. | Y dir. | Z dir. | |
| 2 | 0.278 | 3.602 | 10.0% | 45.6% | 0.0% |
| 6 | 0.184 | 5.423 | 9.9% | 0.4% | 0.0% |
| 22 | 0.134 | 7.484 | 2.8% | 0.4% | 0.0% |
| 24 | 0.117 | 8.565 | 0.0% | 0.0% | 21.9% |
| 38 | 0.090 | 11.156 | 5.7% | 5.6% | 0.0% |
Similar results have been derived for other base restrain condition, but them have not been reported here for the sake of brevity.
6. UPDATING OF THE FE MODEL AND EVALUATION OF THE STRESSES
It has to be stressed that the natural frequencies derived from the FE model slightly differs from those obtained by the experimental dynamic tests and an updating of the model is needed. In this section a simple procedure to update the model will be outlined and the stress distribution will be estimated both in case of fixed support and when radial displacements are allowed.
Firstly, the main arches of the dome were fixed at the base. In this way, horizontal displacements are not allowed as it is in the actual condition. Then, the steel Young’s modulus has been varied until the first natural frequency of the FE model matched the experimental one. This condition has been attained when E = 223000 MPa and this value has been used to evaluate the stress in the main arches in the present condition.
Then, in order to evaluate how the stresses distribution in the main arches were influenced by the possibility of having radial displacements, the supports at the base of main arches have been modeled as slides (radial translations are allowed but rotations are prevented). The analytical model thus obtained is representative of the original support conditions.
In the Figs. (21, 22) the stress distribution along one of the main arches has been reported in terms of eccentricity (i.e. the ratio between the bending moment and the axial force) and of maximum stress with reference to fixed support and slide support at the base. These figures clearly show that in the original support condition, namely when radial displacements are allowed, a reduction in terms of stress can be appreciated.
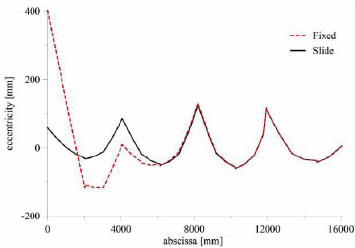
Eccentricity in one of the main arches for fixed support and slide support at the base.

Maximum stress in one of the main arches for fixed support and slide support at the base.
CONCLUSION
The paper provides the results of an experimental dynamic identification carried out on the iron structure of the dome of the “Teatro Massimo” in Palermo (Italy). The main purpose was the estimation of the major stress state generated on the primary structural elements of the dome due to a variation of the behaviour of the base supports (because of an advanced state of oxidation the sliding of the supports was constrained). The response of the dome under impulsive loads was recorded by a system of accelerometers and used to calibrate a finite element model for the estimation of the current stress state influenced by the new boundary conditions.
These experimental results allowed to quantify the increase of stress arising from the fact that the rollers at the base of the arches were no longer able to accommodate the thermal expansion of the structure.
The use of noninvasive and nondestructive experimental tests have been proved to be a useful method to structural health monitoring procedures and especially for extensive and fast inspection analyses aiming at sharpening the numerical models of complex structures provide results very adherent to the real behavior of the analyzed system. Such numerical models can therefore be used for an accurate prediction of the structural response and as an aid for all choices related to the maintenance and structural restoration.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTs
Declared none.


