RESEARCH ARTICLE
Assessment of the Seismic Performance for a Low-Code RC Shear Walls Structure in Bucharest (Romania)
Florin Pavel1, *, Radu Vacareanu1
Article Information
Identifiers and Pagination:
Year: 2020Volume: 14
First Page: 111
Last Page: 123
Publisher ID: TOBCTJ-14-111
DOI: 10.2174/1874836802014010111
Article History:
Received Date: 07/01/2020Revision Received Date: 20/03/2020
Acceptance Date: 12/05/2020
Electronic publication date: 29/06/2020
Collection year: 2020

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
Low-code RC shear walls structures house a significant proportion (over 20%) of the inhabitants of Bucharest.
Objective:
In this research, the seismic performance of a low-code reinforced concrete shear walls structure located in various sites in Bucharest (Romania) is assessed.
Methods:
The seismic performance is assessed using both static and dynamic nonlinear time-history analyses, as well as detailed sectional analysis of the RC shear walls.
Results:
The results show that the structure has significant capacity differences in the two principal directions. Moreover, it has been observed that the maximum top displacements obtained from nonlinear time history analyses are larger in the transversal direction.
Conclusion:
Considering the behaviour of such structures during the 1977 Vrancea earthquake, the fact that these structures are already 40 – 50 years old and given the results of some of the analyses shown in this study, it can be concluded that immediate seismic rehabilitation measures are needed in order to correct, at least partially the structural issues of this section type.
1. INTRODUCTION
The Vrancea intermediate-depth earthquake of March 4, 1977 (moment magnitude MW = 7.4 and focal depth h = 94 km) is one of the most important milestones in the development of earthquake engineering and seismic design in Romania. A comprehensive description of the economic and social impact of this seismic event at the national level and for Bucharest, the capital city of Romania, can be found in the papers of Georgescu and Pomonis [1-3].
In the aftermath of the earthquake, a damage survey was performed on a sample of 18000 buildings from various parts of Bucharest [4]. Among the three residential buildings seismically designed that collapsed in Bucharest, one had a structural system consisting of thin Reinforced Concrete (RC) shear walls (section type OD), the second one had a soft and weak ground storey structure [4] and the structural system of the third one consisted in columns and flat slabs.
This section type was extensively built in Bucharest (a total number of 161 individual buildings with more than 8000 dwellings) during the 1960s and 1970s. Out of the total number of 161 buildings, one completely collapsed (by overturning in the transversal direction) and another seven sustained heavy or very heavy damage; nineteen other buildings experienced extensive damage according to the damage survey performed in the aftermath of the earthquake [4]. After the 1977 seismic event, all the damaged structures were only locally repaired (no strengthening was performed) [3] and subsequent damage occurred during the Vrancea seismic events of August 1986 1977 (MW = 7.1 and h =131 km) and May 1990 (MW = 6.9 and h =91 km).
Consequently, in this paper, we aim at evaluating the seismic performance of the OD section type using both static and nonlinear dynamic analyses, as well as detailed sectional analyses of the RC shear walls. In addition, the impact of the angle of incidence on the seismic response of the analysed structure is also assessed. The impact of the angle of incidence on the seismic response of various structural systems has been analysed by other authors considering several engineering demand parameters [5-7].
2. MATERIALS AND METHODS
2.1. Structural Model
The OD section type has a structural system consisting of RC shear walls placed on the two principal orthogonal directions. The analysed building has 11 stories of 2.75 m each and planar dimensions of 11 x 27 m. The design bases shear coefficient is around 2 - 3% of the total weight of the structure (the values are similar for both the P13-63 and P13-70 seismic design codes enforced in Romania at that time). The most important characteristics of the structural system for the OD section type can be summarized as follows:
- The thickness of all the shear walls is 14 cm, leading thus to a ratio of the area of the shear walls to the total floor area of roughly 1.1% in the longitudinal direction and 3.8% in the transversal direction;
- The boundary elements of the transversal shear walls are 22 cm in width and 30 cm in depth;
- The coupling beams have a height of 58 cm (in some cases 28 cm) and a thickness equal with that of the RC shear walls (14 cm);
- The concrete class is in the range C8/10 – C12/15, while the reinforcement consists of smooth bars of steel grade OB37 (similar to S235);
- The cast-in-place RC slabs have a thickness of 12 cm;
- The edge beams have a cross-section of 30 x 30 cm.
The planar layout of the OD section type is shown in Fig. (1). One can notice the existence of a single RC shear wall in the longitudinal direction, as well as the offset of some of the shear walls in the transversal direction.
Some details regarding the reinforcement of the RC shear walls on both principal directions are given in Table 1. It can be noticed that the interior transversal shear walls have no continuous vertical or horizontal reinforcement (with the exception of some local reinforcement bars) for stories 4 – 10. The reinforcement at the top storey was conceived to withstand the stresses induced by thermal actions over the roof slab. Moreover, the boundary elements of the shear walls have only Φ6 stirrups placed at 30 cm in most of the cases.
The reinforcement in the coupling beams consists of most of the cases from 2Φ12 bars placed at the top and at the bottom part of the elements, while the stirrups are Φ6 spaced at 15 cm. The only coupling beams with more reinforcement are the ones from the longitudinal wall which have a reinforcement of 2x2Φ22 (reduced at 2x2Φ16 for the last five stories) and the two coupling beams from the central transversal shear walls whose reinforcement consists of 2x2Φ18 (reduced at 2x2Φ14 for the last three stories). However, the transversal reinforcement consists again of stirrups Φ6 placed at 15 cm apart.
 |
Fig. (1). Planar layout of the OD section type. |
| Direction | Reinforcement Type | |
|---|---|---|
| Vertical | Horizontal | |
| Longitudinal | web - 2Φ10/30 (or 2Φ8/30 for stories 3 – 11) flange - 12Φ12 (or 12Φ10 for stories 3 – 11) |
web - 2Φ8/30 (or 2Φ6/30 for stories 3 – 11) flange – Φ6/30 |
| Transversal – edge RC shear walls | web - 2Φ8/30 flange - 4Φ16 (4Φ14 for storey 2, 4Φ12 for storey 3 – 11) |
web - 2Φ8/30 (or 2Φ6/30 for stories 3 – 11) flange - Φ6/30 |
| Transversal – interior RC shear walls | web - 2Φ8/30 (2Φ6/30 for storey 3 and 11, no vertical reinforcement for stories 4-10) flange - 4Φ12 (4Φ10 for storey 3 – 11) |
web - 2Φ8/30 (2Φ6/30 for storey 3 and 11, no vertical reinforcement for stories 4-10 flange - Φ6/30 |
The eigenperiods associated with the first two eigenmodes of the structure are 0.57 s (translation in the transversal direction) and 0.42 s (translation in the transversal direction), respectively.
3. NONLINEAR STATIC AND DYNAMIC ANALYSES
In order to assess the seismic performance of the analysed structure, both static nonlinear, as well as dynamic nonlinear analyses are performed. This approach was also employed in the study of Repapis [8] considering RC buildings without seismic detailing. The analyses are conducted using the software SeismoStruct [9] and employing the full 3D structural model. Inelastic force-based plastic hinges (concentrating the inelasticity at the ends of the structural elements) are assigned for all the structural elements. The Mander et al. [10] model was applied for the concrete fibres, while the reinforcement is modelled by using the stress-strain relationship proposed by Menegotto and Pinto [11] and implemented by Monti et al. [12].
3.1. Nonlinear Static Analyses
The pushover analysis is performed in both principal directions of the structure. The resulting pushover curves are shown in Fig. (2). as a function of the ratio of the base shear force (V) to the building total weight (W). The significant discrepancy in terms of capacities in the two principal directions of the structure is noteworthy. This is mainly because of the fact that in the longitudinal direction there are two shear walls with extensive flanges, while in the other direction there are only lamellar RC shear walls, some of which are not continuous on both bays of the structure. It can also be observed the fact that the ultimate points on the pushover curves correspond to a Roof Drift Ratio (RDR) of about 0.5%.
 |
Fig. (2). Comparison of the pushover curves in the two principal directions of the OD section type. |
3.2. Spectral Analysis
The Nonlinear Time History Analyses (NTHAs) are performed using the two horizontal components recorded at INCERC station in the eastern part of Bucharest during the Vrancea earthquake of March 4, 1977. Besides the nonlinear time history analyses conducted with the as-recorded horizontal components, additional analyses are performed considering the rotated components. The pair of horizontal components originally recorded at INCERC station were rotated in the clockwise direction every 5° between 0° and 180° leading thus to more than 30 individual time series. This type of analysis was also applied by Pavel and Nica [13] in the case of regular shear walls structures designed according to the most recent version of the Romanian seismic design code. The mean and mean ± one standard deviation acceleration and displacement response spectra for all the rotated components are illustrated in Fig. (3).
The simplified method of Verdugo et al. [14] is applied in order to evaluate the damage levels (in terms of roof drift ratio) sustained by the OD section type when subjected to the horizontal components recorded at INCERC station during the Vrancea 1977 earthquake. In addition, the damage levels associated with the ground motions recorded during the subsequent Vrancea seismic events of 1986 and 1990 are also assessed using the same method. The core of the method is the relation between the lateral displacement and the fundamental eigenperiod of the structure. Thus, the displacement at the top of the structure is in Equation 1 [7]:
 |
(1) |
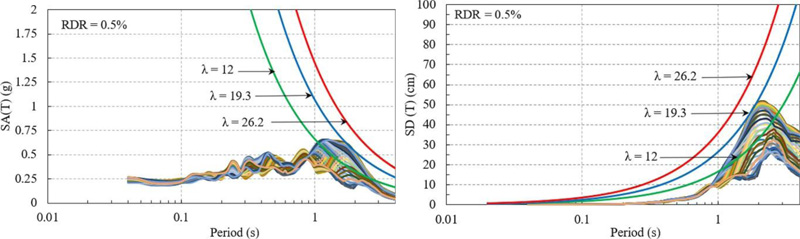
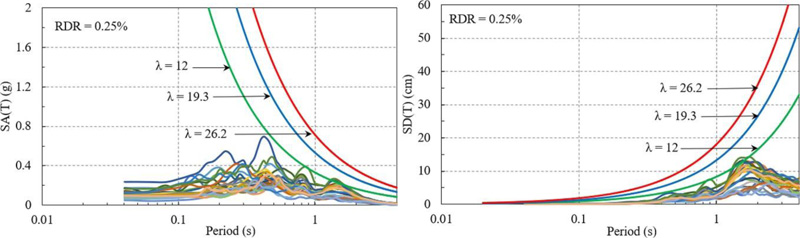
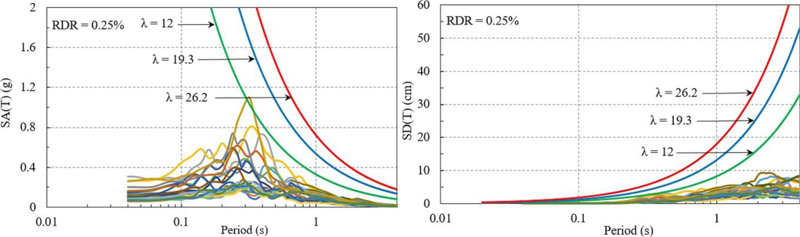
where T is the fundamental eigenperiod of the structure in the considered direction, 2.75 is the story height of the OD section type, λ is a parameter used for the simplified estimation of the period as a function of the number of stories (its value is to be determined subsequently) and RDR is a threshold for the roof drift ratio. The values of the parameter λ are taken as 11 (the number of stories)/0.57 (first eigenperiod in the transversal direction) = 19.3 for the transversal direction and 11/0.42 = 26.2 for the longitudinal direction. A smaller value λ = 12 which leads to a fundamental eigenperiod of 0.92 s is also used in the analysis for comparison purposes.
In Fig. (4) the demand is illustrated as the acceleration and displacement response spectra for all the rotated components of the ground motion recorded at INCERC station during the Vrancea intermediate-depth earthquake of March 1977. In addition, the threshold spectral acceleration and displacement obtained for a roof drift ratio RDR = 0.5% are also shown in order to better evaluate the impact of the rotated horizontal components. The limit RDR = 0.5% was taken based on the results of the pushover analysis shown in the previous section of the paper. It is obvious that the demand imposed by these ground motion recordings is smaller than the limit RDR = 0.5% even for the more flexible direction of the structure (the transversal direction). It can be noticed that the displacement demand imposed by these rotated ground motion recordings reaches and even exceeds the limit RDR = 0.5% only for long-period structures both for λ = 12 and λ = 19.3.
The same type of analysis was applied for the ground motions recorded in the Bucharest area during the Vrancea intermediate-depth earthquakes of August 1986 and May 1990. The results are shown in Fig. (5) and Fig. (6) and in this case, the spectral acceleration and displacement obtained for an RDR = 0.25% are also shown in order to better evaluate the impact of the rotated horizontal components. It is noticeable the fact that the 1986 earthquake imposed larger displacement demands than the 1990 earthquake. However, the displacement demand corresponding to the limit RDR = 0.25% is reached only in the case of the more flexible structure with λ = 12. Thus, it can be concluded that the damage level induced to this section type by the Vrancea intermediate-depth earthquakes of August 1986 and May 1990 is much smaller than the one due to the prior seismic event of March 1977.
3.3. Nonlinear Time History Analyses
The first series of nonlinear time history analyses were conducted using as input the rotated components of the ground motion recorded at INCERC station during the Vrancea intermediate-depth earthquake of March 4, 1977. The set of rotated ground motions is the same as the one used in the previous section of this paper (Fig. 7). illustrates the variation of the maximum top displacement as a function of the rotation angle of the horizontal components. It can be noticed that there are some particular angles for which the displacement in the transversal direction is much larger as compared to the longitudinal one. It is worthy to mention that the rotation angle is measured clockwise with respect to the North direction.
The mean top displacement on the longitudinal direction is 7.6 cm and a coefficient of variation of 0.24, while on the transversal direction the mean top displacement is 9.7 cm with a coefficient of variation of 0.40 (almost double to the one for the longitudinal direction).
In the aftermath of the March 1977 Vrancea earthquake, a damage survey was conducted on a sample of 18000 buildings situated in Bucharest, among which one finds all the OD section type structures. The collected data are summarized in the monograph of the earthquake [4]. The collected data refers to mean damage degree (on a scale from 0 to 5, 0 for no damage and 5 for collapse) and its standard deviation as a function of the position and orientation of the building. As reported by Sandi [15], the adapted MSK methodology was used in Bucharest for the quantification of the damage degree. Fig. (8) shows the variation of the mean damage degree as a function of the building orientation for the two principal directions of the structure. The results show a smaller variability of the mean damage degree on the longitudinal direction as compared to the transversal one. In addition, the larger mean damage degrees observed in the transversal direction in Fig. (8). are somewhat similar to the directions of the maximum top displacements shown in Fig. (7).
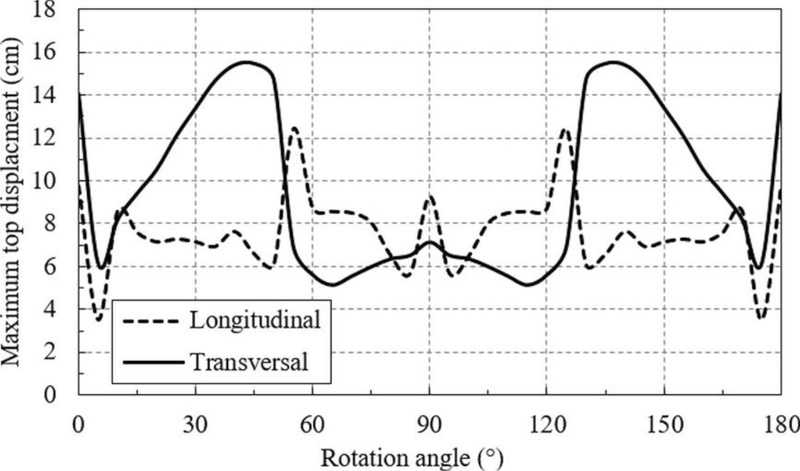 |
Fig. (7). Maximum top displacement on both principal directions as a function of the rotation angle of the horizontal components. |
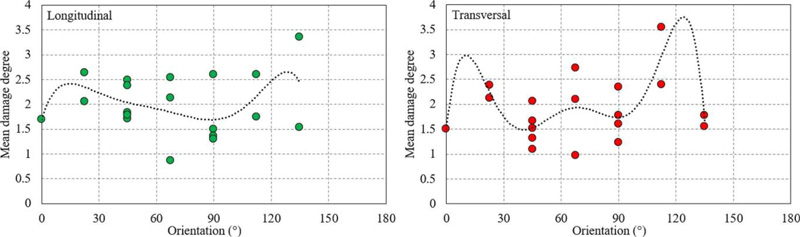 |
Fig. (8). Mean damage degree as a function of the building orientation for the longitudinal direction (left) and for the transversal direction (right). The plots are based on the damage survey performed after the Vrancea 1977 seismic event [4]. A polynomial trendline shown with a dashed line is also fitted on the two plots. |
3.4. IDA Analyses
The Incremental Dynamic Analyses (IDA) [16] are performed separately on the two principal directions of the structure using a ground motion dataset consisting of 20 horizontal components recorded in the Bucharest area during the Vrancea intermediate-depth earthquakes of March 1977, August 1986 and May 1990. The same ground motion dataset was employed in the analyses performed in the study of Pavel et al. [17]. The absolute acceleration response spectra, as well as the median, 16th and 84th percentiles are illustrated in Fig. (9).
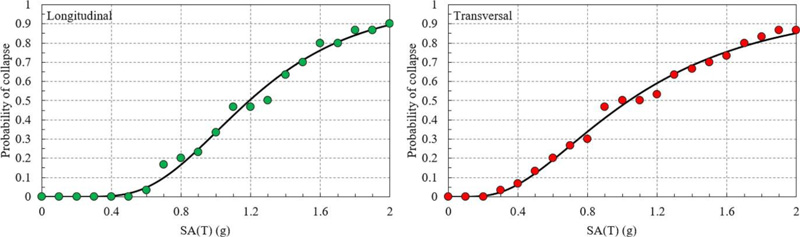
Through this type of analysis, the numbers of collapses (defined as a numerical instability) were identified as a function of the level of the demand (in this case the spectral acceleration corresponding to the fundamental eigenmodes on the two principal directions of the OD section type). A lognormal Cumulative Distribution Function (CDF) was fitted on the results of the incremental dynamic analysis using the procedure of Baker [18]. The probabilities of collapse and the fitted lognormal CDF are shown in Fig. (10)., while the two parameters defining the function are given in Table 2. The much larger variability in terms of logarithmic standard deviation β on the transversal direction as compared to the longitudinal one is also noteworthy. As a consequence, the probability of collapse is much larger in the transversal direction of the structure.
Considering a spectral acceleration of 0.4 g, which is the mean value obtained from all the rotated components of the ground motion recorded at INCERC station during the Vrancea 1977 earthquake, the collapse probability of the OD section type is 0.4% on the longitudinal direction and 6.4% on the transversal direction. It has to be highlighted again the fact that the collapse of the OD section type during the 1977 Vrancea earthquake occurred in the transversal direction.
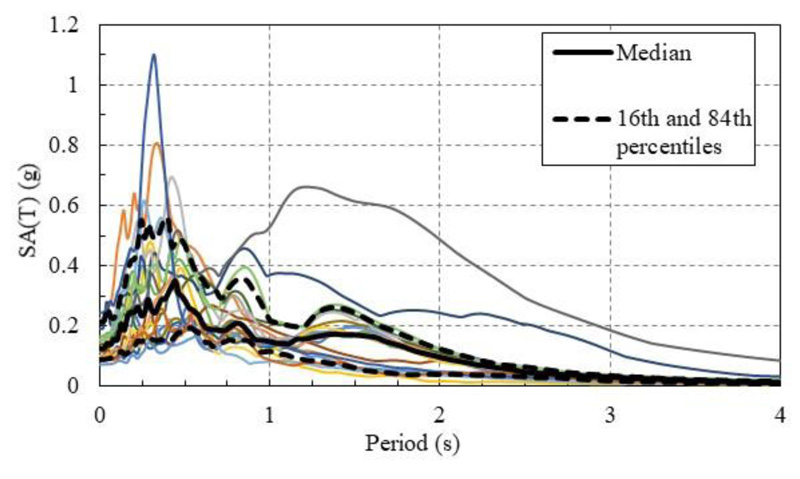 |
Fig. (9). Absolute acceleration response spectra, median, 16th and 84th percentiles for the ground motion recordings used in IDA. |
| Direction | Parameters of Lognormal Fragility Function | |
|---|---|---|
| Median θ (g) | Logarithmic Standard Deviation β | |
| Longitudinal | 1.19 | 0.41 |
| Transversal | 1.02 | 0.63 |
4. RESULTS AND DISCUSSION
4.1. Experimental Results
A series of five experimental tests were performed at the Building Research Institute in Tsukuba (Japan) and at the Technical University of Civil Engineering Bucharest in the mid-2000s in the framework of the Japan International Cooperation Agency (JICA) Project in Romania [19]. Three of the specimens were designed so as to fail in shear, while the other two exhibited a flexural type of failure. The specimens measured 1.8 m x 1.8 m and had a thickness of 10 cm. The concrete class and the reinforcement were similar to those used for structures built before 1977. The Axial Load Ratio (ALR) was 0.13 for four of the specimens and 0.26 for the last one. The first four specimens did not have horizontal or vertical web reinforcement with the exception of a beam placed at mid-height. The last specimen had a similar percentage (0.30%) of horizontal and vertical web reinforcement. The vertical reinforcement from the boundary elements consisted of either 8Φ12 bars for the first three specimens or 4Φ8 for the last two specimens.
Two methods namely, the modified UCSD method proposed by Krolicki et al. [20] and which is based on the original UCSD method of Kowalsky and Priestley [21] and the Disturbed Stress Filed Model (DSFM) proposed by Vecchio et al. [22] and implemented in VecTor2 [23] and VecTor4 [24] are applied using as input data the above-discussed experimental results.
The proposed relation for assessing the shear strength capacity from the modified UCSD shear model in equation 2 [20, 21].
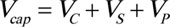 |
(2) |
where VC- is the shear component taken by the concrete, VS is the shear component taken by the horizontal reinforcement and VP is the component due to the axial force. The parameters necessary for the computation of each of the three components for RC shear walls are given in the paper of Krolicki et al. [20] and will not be discussed hereafter.
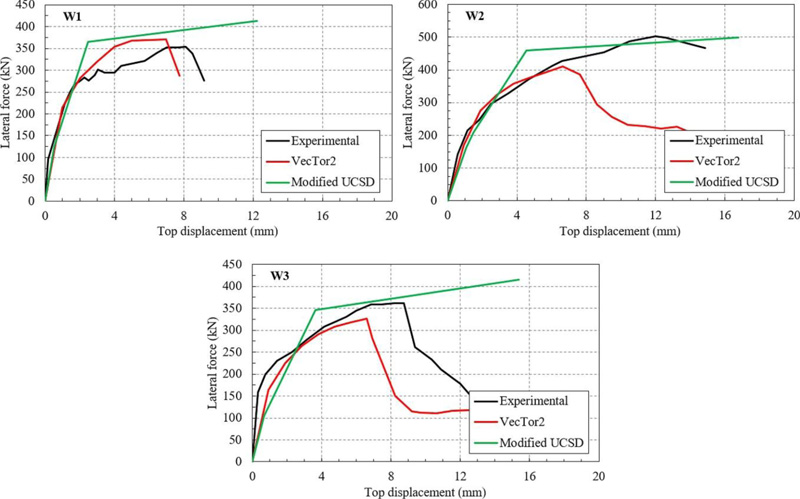 |
Fig. (11). Comparison between the experimental and numerical results for the first three specimens which failed in shear. |
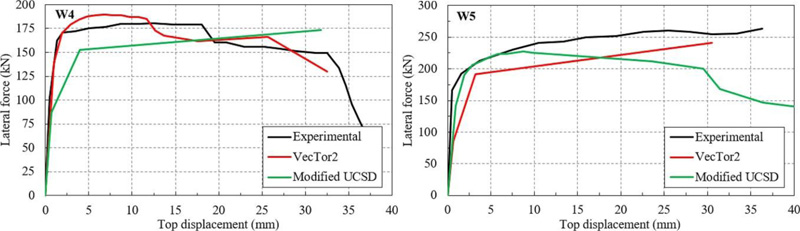 |
Fig. (12). Comparison between the experimental and numerical results for the last two specimens which failed in flexure. |
VecTor2 [23] and VecTor4 [24] are nonlinear finite element modelling software able to capture the 2D and 3D behaviour, respectively, of RC elements. Both of these programs have already been used in many studies referring to the modelling of RC shear walls [25-27]. The basic material models from VecTor2 [23] were used in order to model the behaviour of the five experimental RC shear walls. The comparisons between the experimental value (envelope of the results) and the numerical ones for the first three RC shear walls (the ones which failed in shear) are shown in Fig. (11). The comparisons between the experimental results and the numerical ones for the last two specimens (which failed due to flexure) are shown in Fig. (12).
The modified UCSD method [20] is capable of predicting the failure mode of each of the five specimens. In addition, it can be seen from both Fig. (11). and Fig. (12). that both methods are able to replicate quite accurately in some cases the envelope of the force-displacement curve obtained from the experimental results. As such, both methods are to be applied subsequently in order to evaluate the failure modes of some of the RC shear walls of the OD section type structure.
4.2. Numerical Analyses
The numerical analyses shown in this section aim at assessing the failure mode and the capacity of some of the individual RC shear walls of the OD section type structure. Three types of RC shear walls namely, two lamellar transversal walls (one edge wall and one interior wall) and the longitudinal one, are to be evaluated numerically using VecTor2 [23] and VecTor4 [24], as well as the modified UCSD method [20].
Fig. (13) shows the force – displacement curves obtained from VecTor2 [23] and using the modified UCSD method [20] for the transversal edge wall (the single individual wall spanning on both bays in the transversal direction) subjected to an axial force level of 3500 kN. It can be observed that both methods provide the same capacity for this shear wall, with failure occurring at a roof drift ratio of around 0.5 – 0.6%. Moreover, the failure mode of this wall is in flexure. The main reasons for this type of failure are related to the fact that the boundary elements are small (22 x 30 cm) and their confinement reinforcement is extremely small (Φ6 stirrups placed at 30 cm).
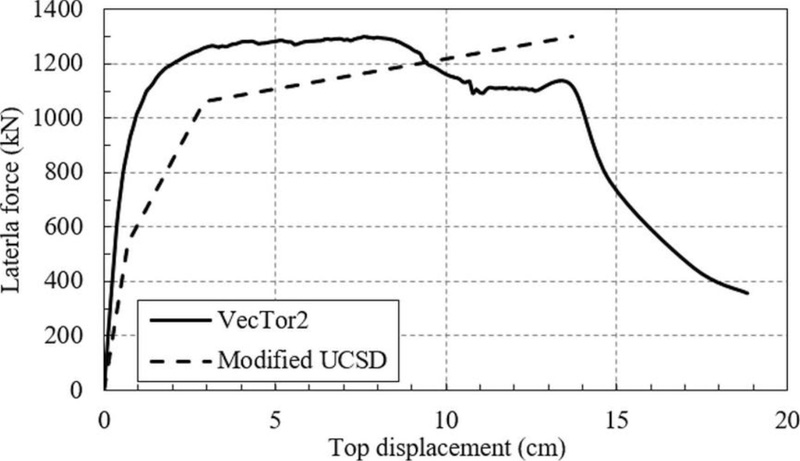 |
Fig. (13). Comparison between the force – displacement curves for the edge transversal wall obtained using the modified UCSD method and VecTor2. |
Fig. (14) illustrated the force-displacement curves for an interior transversal wall also evaluated from VecTor2 [18] and using the modified UCSD method [20]. The axial force level for which the computations are made is 1800 kN. It can be observed that in this case, the failure occurs at larger roof drift ratios (about 0.8%) as compared to the edge RC shear wall. In this case too, the failure mode is due to flexure. However, if the axial force decreases coupled with the reduction of the shear reinforcement along the height of the shear walls, the failure mode changes into a combined flexural and shear failure.
The influence of the axial force level on the two transversal RC shear walls (an edge shear wall and an interior one) is noticeable in Fig. (15). As expected, the ductility decreases with the axial force level, but this decrease is clearly more visible in the case of the edge wall. It is also noticeable the fact that the displacement at which the failure occurs is much smaller for the edge walls and its decrease due to the increase of the axial force is larger than in the case of the interior RC shear wall.
Subsequently, in order to check the biaxial behaviour of the longitudinal wall, the force-displacement curves on the two horizontal directions were computed for the longitudinal wall (only a quarter of it was modelled resulting in practically an L shape RC shear wall). The results of this analysis are shown in Fig. (16). One can notice that as the level of axial force increases, the ultimate displacement reduces and the failure becomes more and more sudden. Moreover, it can be observed that as the axial force increases, the difference in ultimate displacement capacity between the two horizontal directions decreases. It has also been noticed that due to the increased flexural capacity of the longitudinal wall, its failure mode is mainly due to in-plane shear.
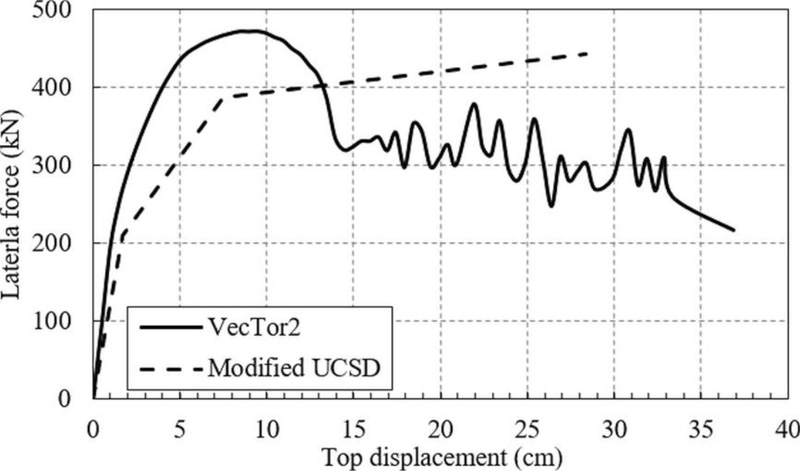 |
Fig. (14). Comparison between the force – displacement curves for the central transversal wall obtained using the modified UCSD method and VecTor2. |
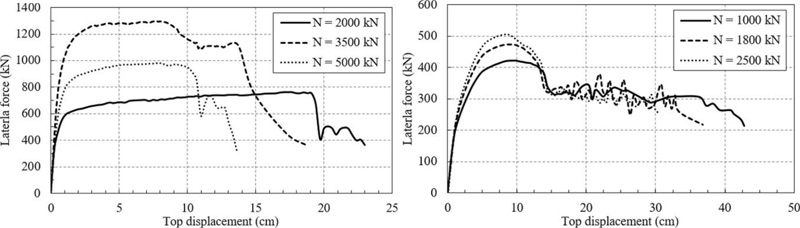 |
Fig (15). Comparison between the force – displacement curves for an edge (left) and an interior (right) transversal shear wall as a function of the axial force level. |
CONCLUSION
In this study, the seismic performance of a low-code reinforced concrete shear walls structure, namely the OD section type is assessed. This section type was seismically designed (even for very low base shear coefficients) and built in Bucharest in the period before the large Vrancea intermediate-depth earthquake of March 4, 1977. This particular seismic event is one of the most important milestones in the development of seismic design in Romania. The most important observation of this study can be summarized as follows:
- There is a very large discrepancy in terms of shear walls’ area on both principal directions of OD project type structures. However, the capacity of the analysed structure is much larger in the longitudinal direction as compared to the transversal one. The ultimate point on the pushover curves on both principal directions corresponds to a roof drift ratio of about 0.5%.
- The displacement demand imposed by the rotated horizontal components of the ground motion recorded at INCERC station during the Vrancea intermediate-depth of March 4, 1977 are smaller than the limit RDR = 0.5% even for the more flexible direction of the OD section type (the transversal direction). It is observed the fact that the displacement demand imposed by the same rotated ground motion recordings reaches and even exceeds the limit RDR = 0.5% only for long-period structures.
- The analyses reveal much smaller damage levels induced to the OD section type by the Vrancea earthquakes of August 1986 and May 1990, as compared to the event of March 4, 1977.
- The collapse probability of the OD section type is 0.4% on the longitudinal direction and 6.4% on the transversal direction for the mean value of the spectral acceleration of the rotated horizontal components of the ground motion recorded at INCERC station during the Vrancea intermediate-depth of March 4, 1977.
- The mean top displacements obtained from the rotated horizontal components of the ground motion recorded at INCERC station during the Vrancea earthquake of 1977 is 7.6 cm and a coefficient of variation of 0.24 on the longitudinal direction, while on the transversal direction the mean top displacement is 9.7 cm with an almost double coefficient of variation of 0.40. The directions corresponding to the maximum top displacements coincide to a certain extent with the building orientations for which the largest mean damage degree was observed in the survey performed after the March 4, 1977 Vrancea intermediate-depth earthquake.
- The detailed investigation into the behaviour of some individual shear walls of the OD section type has revealed the fact that the displacement at which the failure occurs is much smaller for the edge walls and its decrease due to the increase of the axial force is larger than in the case of the interior RC shear wall. Thus, it is likely that the collapse of the OD section type during the Vrancea intermediate-depth earthquake of March 4, 1977 was initiated through the flexural failure of the boundary elements in the edge transversal RC shear walls.
The main conclusion of the study is that considering the behaviour of the analysed type of structures during the Vrancea 1977 event, the fact that these 40 – 50 years old structures are in large numbers in Bucharest and thus house many people and given the results of some of the analyses shown in this study, immediate seismic rehabilitation measures are needed in order to correct, at least partially the structural issues of this section type, in order to prevent their local or total collapse.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The first author wishes to thank Dr. Trevor Hrynyk for providing the VecTor4 software used in some of the analyses performed in this paper, as well as for its guidance for performing the numerical analyses with VecTor4. The constructive comments from two anonymous Reviewers and from the Editor-in-Chief are greatly appreciated as they helped us to considerably improve the quality of the original manuscript.