RESEARCH ARTICLE
Nonlinear Dynamic Analysis of Masonry Buildings and Definition of Seismic Damage States
A.J. Kappos1, 2, *, V.K. Papanikolaou2
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
Issue: Suppl 2: M2
First Page: 192
Last Page: 209
Publisher ID: TOBCTJ-10-192
DOI: 10.2174/1874836801610010192
Article History:
Received Date: 15/1/2015Revision Received Date: 15/5/2015
Acceptance Date: 1/7/2015
Electronic publication date: 31/05/2016
Collection year: 2016

open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
A large part of the building stock in seismic-prone areas worldwide are masonry structures that have been designed without seismic design considerations. Proper seismic assessment of such structures is quite a challenge, particularly so if their response well into the inelastic range, up to local or global failure, has to be predicted, as typically required in fragility analysis. A critical issue in this respect is the absence of rigid diaphragm action (due to the presence of relatively flexible floors), which renders particularly cumbersome the application of popular and convenient nonlinear analysis methods like the static pushover analysis. These issues are addressed in this paper that focusses on a masonry building representative of Southern European practice, which is analysed in both its pristine condition and after applying retrofitting schemes typical of those implemented in pre-earthquake strengthening programmes. Nonlinear behaviour is evaluated using dynamic response-history analysis, which is found to be more effective and even easier to apply in this type of building wherein critical modes are of a local nature, due to the absence of diaphragm action. Fragility curves are then derived for both the initial and the strengthened building, exploring alternative definitions of seismic damage states, including some proposals originating from recent international research programmes.
1. INTRODUCTION
Analysis of unreinforced masonry (URM) buildings for seismic assessment purposes is typically carried out using the nonlinear static (pushover) method involving planar (2D) and, less often, 3D models. In addition to equivalent frame models, currently available analytical tools for URM also include finite element models based on isotropic / orthotropic homogeneous nonlinear material, or even heterogeneous nonlinear material assumptions. Furthermore, discrete element formulations are available, focussing on the nonlinear behaviour of joints between masonry units. The high computational cost and high analytical skills required for implementing continuum or discrete finite element models, make equivalent frame models the most popular choice for practical nonlinear analysis of URM structures. An evaluation of equivalent frame models for linear and nonlinear analysis of URM buildings and some comparisons with continuum models can be found in [1]. This method has sometimes been supplemented by limit analysis involving simplified models of critical components of the structure, aiming at the estimation of the ultimate load that can be sustained for a postulated collapse mechanism. Nonlinear dynamic response history analysis has been a far less popular tool in the case of URM structures, due to the absence of appropriate models, software, and expertise, not so much in carrying out the analysis but in interpreting its results, which are both voluminous and difficult to translate into global damage description.
Significant work on nonlinear analysis of URM buildings has been carried out in the last few years with a view to (i) refining the available models and the associated software, and (ii) interpreting the results of nonlinear analysis for the purposes of identifying the state of damage in the building, which will lead to a meaningful assessment and guide the design of strengthening measures, wherever needed. A substantial part of this work has been carried out in Italy [2-6], wherein large stock of heritage URM structures is subjected to a high level of seismic hazard. A notable recent development is a macroelement model for the nonlinear static and dynamic analysis of URM buildings [2, 3] that was implemented in the computer code TREMURI; the element accounts for both flexural/rocking and shear failure modes.
Whereas the definition of seismic input (accelerograms) for response history analysis has now become part of practical analysis due to the development of large ground motion databases (in Europe, Japan, and the US) and of appropriate software for record selection [7], the definition of seismic action in nonlinear static analysis is much more of a problem, especially in the common case that the URM building does not have rigid floor diaphragms. Code-type documents [8, 9] suggest the use of both a ‘uniform’ (proportional to the mass distribution) and a first mode based or ‘triangular’ force pattern, which is a conservative choice as the most unfavourable response quantities among the two patterns are used for the assessment. To overcome over conservatism, heuristic approaches have been put forward; for instance, a force pattern was suggested [3] that is proportional to the deformed shape of the building, estimated from a preliminary nonlinear analysis using a nominal pattern (such as the triangular one). It is worth noting that if this approach is used in a 3D analysis, additional constraints (also heuristic) have to be introduced, i.e. the results from the uniform and triangular patterns are used to bound the force pattern resulting from the inelastic deformed shape. A more rigorous, still approximate, procedure, called ‘modal pushover’ analysis (MPA), has been proposed in [10] for concrete buildings and later extended to concrete bridges [11]. In this method, nonlinear static analysis is carried out separately for the load pattern corresponding to each significant mode of the structure (usually 2-3 modes in each direction are sufficient [10,11]) and the results are combined statistically (SRSS or CQC), with the exception of member forces and moments that are calculated from the pertinent constitutive laws (e.g. moment vs. rotation) from the corresponding deformations. So far this powerful technique has not been used for URM buildings, as several practical problems arise.
Equally important to the procedure for carrying out the nonlinear analysis is the interpretation of its results in the context of seismic assessment, in particular for the description of damage states or performance levels, which is an essential step in the assessment procedure and its outcome is used to select the intervention scheme for the URM building [12]. Even more difficult than defining damage for the purposes of the design of interventions (strengthening measures) is the definition of damage for the purposes of fragility analysis, i.e. for the derivation of sets of fragility curves, each corresponding to a certain damage state. Of particular difficulty in this respect is the derivation of fragility curves for states close to collapse that are of paramount importance in loss scenarios, as they are the ones used in estimating human casualties and buildings that have to be demolished. A comprehensive set of criteria for defining damage or performance levels has been proposed in the framework of a recent European research project [6]; it is noteworthy that most of these criteria are predominantly heuristic (see further discussion in §2.2).
The main objective of this paper is to propose an analysis procedure that can be used for the seismic assessment of realistic URM buildings (stone or brick), including those that do not have rigid floors. Like other recent studies accounting for the inelastic response of masonry members, the proposed procedure involves an equivalent frame model of the building, but unlike the other studies, nonlinear dynamic response history (rather than static pushover) analysis is used, for a set of input ground motions (accelerograms) scaled to different levels of earthquake intensity, so that the response up to failure can be captured. Results of this type of analysis are then used for deriving fragility curves for different damage states using alternative sets of definitions of these damage states on the basis of inelastic deformation criteria. The methodology is applied to a masonry building representative of Southern European practice, which is analysed in both its original condition and after applying retrofitting schemes typical of those implemented in pre-earthquake strengthening programmes.
2. METHODOLOGY
The procedure proposed herein can be used for most types of stone or brick masonry buildings, but is deemed to be particularly suitable for those with timber floors (with or without some small-size steel beams) and roof, whose behaviour is substantially different from that of URM buildings with reinforced concrete floors; this type of flexible horizontal structures is very common in older masonry buildings (generally the pre-World War II ones). As will be shown in §3, even single-storey buildings without rigid diaphragms are characterised by the absence of a predominant mode in either principal direction and hence render particularly cumbersome the application of popular and convenient nonlinear analysis methods like the static pushover analysis.
2.1. Nonlinear Analysis of Realistic URM Buildings
In the absence of a predominant mode in the direction of the analysis (leaving aside for the time being the issue of simultaneous application of earthquake actions in both principal directions) one can in principle, apply modal pushover analysis [10]; this means that the number of independent pushover analyses to be carried out in each direction is dictated by the number of modes that contribute up to a substantial fraction of the total mass (around 80%). Unfortunately, unlike what happens in reinforced concrete buildings and bridges wherein 2-3 modes are typically sufficient for capturing the horizontal response, in 3D URM buildings without rigid diaphragms even 20 or 30 modes might not be enough for activating a substantial part of the building mass, since the modes are of a local nature. Moreover, the location of critical deformations is generally different in each mode, which means that resistance curves (also called pushover curves) have not only to be drawn with respect to different monitoring points (this is also the case with bridges [11]) but, if they are plotted in terms of the total base shear (as commonly done) they might not even have a physically sound shape (i.e. one without snap backs). Finally, results from all these separate analyses have to be statistically combined (e.g. SRSS), which gives rise to a number of problems and inconsistencies, especially in the case of member forces (e.g. pier shears). On top of the theoretical problems, implementation of such a procedure is as yet not ‘automatised’, hence results from different nonlinear analyses have to be combined ‘manually’ (i.e. using a spreadsheet). These problems can be overcome if dynamic response history analysis, which captures the effect of all modes, is used, as described in the following.
The specifics of an analysis procedure depend on the purpose of the analysis; for instance, in an extreme case that only the response up to first (or minor) cracking is sought, linear elastic analysis would be the preferred method. Here, the ultimate goal is the derivation of fragility curves encompassing response up to failure, hence both the models and the input to be used should account for this requirement.
Starting from the input, the available options are:
- Use of a fixed suite of recorded ground motions consistent with a hazard scenario (i.e. magnitude and epicentral distance within reasonable bounds, e.g. M=6÷6.5, R=20÷50 km, and a specific ground type, usually defined by a range of shear wave velocities, e.g. Ground B according to Eurocode 8 [9], with vs=360÷800 m/s). Instead of, or in addition to, the above, one can also use as a selection criterion the similarity of the response spectra of the recorded motions and a target spectrum, either a code specified one or a site-specific one derived from probabilistic hazard analysis. Currently available software packages like ISSARS [7] use such criteria to select from international databases of recorded motions. As an alternative to this procedure one can use artificial, spectrum-compatible records, whose frequency content might be not very realistic, but the procedure is quicker than the proper selection of recorded motions and (importantly) the number of records needed is substantially less; this convenient option is not allowed when the goals of the analysis include the estimation of the variability in the response quantities. The suite of (natural or synthetic) records is scaled to increasingly higher values of peak ground acceleration (PGA), until ‘failure’ is predicted by the analysis. This procedure is commonly referred to in the recent literature as incremental dynamic analysis (IDA) [13], but the concept of scaling a set of records and calculating the evolution of key response parameters (like drift or ductility factor) was introduced much earlier [14]. It is worth mentioning herein that there are some previous studies [15] where nonlinear response-history analysis is applied for a number of increasing intensity levels to masonry buildings, but the damage and failure criteria used are stress, rather than deformation based as herein.
- Use of different suites of ground motions at each ground motion intensity level; this technique, commonly referred to as "Multiple stripe analysis" [16] allows for differences in anticipated properties of low-intensity and high-intensity motions to be captured via ground motion selection, but requires additional effort in both ground motion selection and structural analysis; it will not be further considered herein, since the computational effort in the present analysis is quite heavy even if the previous option for record selection is adopted.
With regard to the model, as discussed in the previous section, the clearly preferred choice in the case of 3D analysis of entire URM buildings is the equivalent frame model. Fig. (1) shows such a model for the typical substructure found in URM buildings, a wall with openings for doors and windows; thicker lines in the model represent the rigid offsets, while dashed lines correspond to piers and spandrels, both of them modelled using beam-column elements.
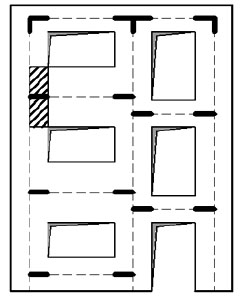 |
Fig. (1). Force-displacements curves for different values of C (α=1). |
The nonlinear behaviour of both piers and spandrels is described in the simplest possible way by introducing concentrated plastic hinges at the element ends; for 3D analysis four hinges are introduced in each pier (top/bottom for both directions), while two hinges are introduced in each spandrel (acting in their strong direction). The point hinge simplification permits the use of standard software packages for nonlinear analysis of structures like SAP2000 [17] that was used in the present study. The nonlinear constitutive laws (moment vs. rotation) to be used for each hinge should properly account for the pertinent failure modes, i.e. in addition to flexure, inelastic shear response should be captured. It is noted that in this relatively simple approach connections between intersecting orthogonal walls are modelled as rigid, hence possible separation in these locations cannot be captured.
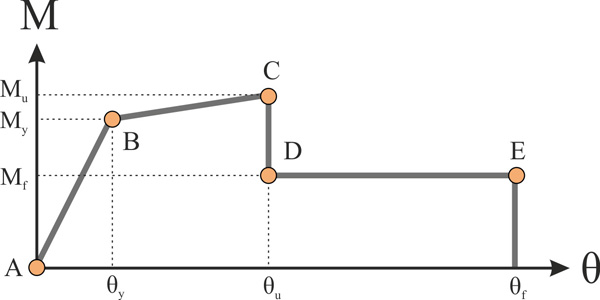 |
Fig. (2). Backbone curve of M-θ relationship for equivalent frame members. |
The backbone moment (M) vs. rotation (θ) curves for pier hinges (Fig. 2) include both pre and post-peak response and were calculated using the method suggested in [18], which accounts for both flexure and shear mechanisms. This method combines a phenomenological closed-form solution for the flexural response with an empirical model (calibrated against results from tests on URM walls and buildings [19]) for inelastic shear. The M-θ curves resulting from this model are then recast in a bilinear form, to define part ABC of the multilinear constitutive law shown in Fig. (2). The strength is calculated from standard flexural analysis but is capped if the moment corresponding to the development of the shear strength in the pier is lower; the corresponding rotation results from the bilinearization of the initially derived curve. The rotation at ultimate (point C) θu is taken equal to 5.3‰ (mean value from tests reported in [19]) when shear failure prevails, while point E is taken as θf = 2θu and 3θu for in plane and out of plane response, respectively; the residual strength is taken equal to Μf = 0.6My, following the ASCE/SEI [8] recommendations for URM.
For spandrel hinges, the analytical procedure suggested in [20] and experimentally validated in [21] was followed. The following relationships were used to estimate the spandrel strength:
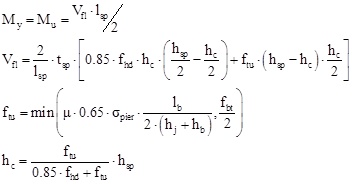 |
(1) |
where:
Μy: flexural strength (point B in Fig. 2)
Vfl: shear force corresponding to My
hsp: depth of spandrel section
tsp : thickness of spandrel
lsp: span of spandrel
fhd: compressive strength of masonry perpendicular to the head joints (fhd ≈ 0.5∙fm, where fm is the ‘standard’
compressive strength, i.e. perpendicular to the bed joints)
ftu: tensile strength of masonry
σpier: compressive stress on the pier supporting the spandrel (resulting from gravity loading)
μ: friction coefficient (taken equal to 0.5)
lb: width of masonry unit
hb: depth of masonry unit
hj: thickness of mortar joint; taken as lb/(hb+hj)
The rotation values in the model of Fig. (2) were estimated as follows:
θy= (My∙(lsp)/(6EI) assuming fixed-ended spandrel (Ε ≈ 750∙fm)
θu = 0.004∙lsp/hsp from ASCE/SEI [8]
θf = 0.008∙lsp/hsp from [8]
Mf = 0.6∙Mu from [8]
In the absence of a more refined hysteresis model in the available software, elastoplastic kinematic behaviour is assumed under seismic loading, for both piers and spandrels; clearly, pinched behaviour and cyclic or ‘within-cycle’ strength degradation, would have been more appropriate, for both flexure/rocking and shear. As shown in Fig. (3), the hysteretic moment vs. plastic rotation model used showed satisfactory performance without numerical instabilities, even in members entering deep into the post-peak (strength degradation range).
 |
Fig. (3). Hysteretic M-θ relationship for a pier subjected to seismic action inducing substantial damage. |
Finally, the ground is modelled by a system of springs at the bottom of each pier, whose stiffnesses Kx, Ky, and Kz were defined according to [8].
2.2. Interpretation of Nonlinear Analysis Results
The focus here is on processing and interpreting the results of nonlinear response-history analysis to define the state of damage in a URM building; the ultimate goal is to define damage thresholds, i.e. the values of the selected response parameter at which the building enters into a certain damage state. The damage thresholds are then associated to specific intensity measures, to derive fragility curves in the standard form, i.e. P(D>DSx|I) vs. I, where I is the earthquake intensity measure (typically the ground or spectral acceleration) and P(D>DSx|I) is the probability that the damage exceeds the threshold of damage state x, given an intensity I. In the following 4 damage states will be considered, in line with most recent studies; the definition of these damage states (DS) is given in Table 1, where there is also a broad correlation of DS with performance levels suitable for ordinary URM buildings (i.e. not those of high importance). Note that buildings that do not exceed the threshold of DS1 are classified as undamaged (DS0), which implies essentially elastic response (that in practice will include some minor cracking, due to either seismic or ‘non-seismic’ actions).
A convenient way to define the damage states in buildings is in terms of inter storey drift; this was in fact proposed in [2] wherein the drift values shown in the 4th column of Table 1 were proposed for URM buildings whose walls are expected to fail in-plane (assuming out-of-plane failures are prevented through proper wall connections and/or provision of ties). It is worth noting the low drift values (especially for DS2), which apparently apply to buildings without foundation compliance effects. Comparing with values proposed in HAZUS [22], the differences in the drift at collapse are dramatic (in HAZUS ultimate drifts vary from 0.61% for 3-storey buildings to 1.8% for single-storey buildings, the latter being more than 3 times the value suggested in [2, 19]). The first author and his co-workers [23] were the first to propose the definition of damage states for URM buildings in terms of displacement quantities on the pertinent pushover curve (Δy, the yield displacement and Δu the ultimate displacement, defined at a predetermined drop in strength in the post-peak range of the response). The threshold values suggested in [23] are summarised in the 5th column of (Table 1). This approach is more appropriate than the one proposed in [2] in that structure-specific displacements, rather than universally applicable drifts, are used to define the damage states; this, of course, makes it more cumbersome, in that the pushover curve has to be estimated prior to deriving fragility curves, but this is generally considered as reasonable effort today. In a more recent study in Italy [5] alternative criteria were explored for defining DS1 to DS3 in nonlinear dynamic analysis; the finally suggested criteria are given in the last column of Table 1 and they involve pier strength and base shear of the building. It is noted that base shear based criteria are much more convenient to implement in nonlinear static, than in nonlinear dynamic (response-history), analysis.
Synthesis of damage state definitions from the literature.
| Damage state | Description | Associated performance level | Drift (from [2]) |
Displacement from pushover curve (from [23, 24]) |
Shear resistance criteria (from [5]) |
|---|---|---|---|---|---|
| DS1 | Negligible structural damage; low non-structural damage | Immediate occupancy | 1‰ | 0.7Δy | first pier attaining its maximum shear |
| DS2 | Minor structural damage and/or moderate non-structural damage | Damage limitation | 0.7Δy+5(Δu- 0.7Δy)/100 | weighted story drift equals value at the attainment of maximum base shear |
|
| DS3 | Significant structural damage and extensive non-structural damage. | Life safety | 3‰ | 0.7Δy+20(Δu-0.7Δy)/100 | 20% degradation in maximum base shear capacity |
| DS4 | Collapse; repairing the building is not feasible. | Collapse prevention | 5‰ | Δu | - |
In the recently completed PERPETUATE project [6], a multi scale approach was adopted for the definition of damage states, i.e. damage for (most of) the DSs was defined at local (pier or spandrel), macroelement (wall), and global (entire building), level; global criteria were defined on the pushover curve for the building. This is a very appropriate approach and has also been adopted (in a different way than in [6]) in the present study. The PERPETUATE criteria have been tailored to nonlinear static, rather than to dynamic, analysis that is proposed herein. The response parameters used to describe damage (2nd column of Table 2) are: λP-S, the cumulative rate of damage defined as the percentage of piers or spandrels that reached or exceeded a given DS, weighted on the corresponding cross section; θDSx is the interstorey drift for the wall considered, calculated taking into account the contribution of both the horizontal displacement and rotation of nodes; κg is the percentage of the maximum base shear, the values for DS3 and DS4 referring to the post-peak range of the response. As can be seen in the table, ranges of values, rather than single values are suggested for the threshold quantities, e.g. the drift defining DS1 varies from 0.5‰ to 1‰. It is clear that definitions involving percentages of ‘failed’ members, albeit convenient, are inevitably of a heuristic nature, whereas drift-based definitions can account for experimental evidence, wherever available (values in Table 2 are based mainly on [19]). Finally, it is worth noting that different types of URM buildings were studied in [6] and different types of static analysis (pushover or limit analysis) were generally proposed for each type; response-history analysis was not addressed in that study.
Damage state definitions from the PERPETUATE project [6].
| Scale | Damage thresholds | DS1 | DS2 | DS3 | DS4 |
|---|---|---|---|---|---|
| Local | λP-S | 0.025-0.05 | - | - | - |
| Macroelement | θ DSx | 0.5-1.0‰ | 1.5-3.0‰ | 3.5-5.0‰ | 5.5-7.0‰ |
| Global | κG, DSx | ≥0.5 | 0.95-1 | 0.8-0.9 | 0.6-0.7 |
In the light of the critical assessment of previous works, and the fact that the analytical procedure (the characteristics of which are always essential in selecting appropriate damage criteria) involves nonlinear response-history analysis of equivalent frame models with point hinge elements, the present study defines damage state thresholds on the basis of two types of criteria:
Local criterion (member level): Damage states are defined as shown in Fig. (4), with reference to specific points of the M-θ backbone curve; DS1 initiates at the ‘yield point’ (which, in the case of piers, is defined from the bilinearization of the actual M-θ curve, hence in general corresponds to a stage subsequent to first cracking in the member); DS3 initiates at the exceedance of the θu value defined on the basis of test results (see §2.1), while DS2, in the absence of conclusive evidence in the literature, is simply taken halfway between points B and C; finally, DS4 initiates at the end of the M-θ constitutive law, e.g. at θf = 2θu in the usual case that the critical response is in the loading direction (note that records are applied separately in each direction, to have a clear picture of the response).
Global criterion (building level): Given the uncertainty inherent in heuristic criteria, upper and lower bounds were explored, as follows:
- Lower bound (conservative): A series connection system is assumed, i.e. for assigning the building to a global damage state DSx, at least one pier should reach a local damage index DSx (in one or more of its four plastic hinges). As also noted in [6], this approach is adopted when the model is not able to capture the progressive strength degradation in the resistance of the elements; however, the present study adopts a multilinear backbone curve Fig. (2) for URM members, hence this criterion is applied mainly for comparison purposes. Nevertheless, given that members not critical to the overall stability of the building should not play a key role in global damage assessment, spandrels were excluded from the definition of the global damage index; of course, in designing a repair and/or strengthening scheme such failures should be taken into account.
- Upper bound (potentially non-conservative): For assigning a global damage index DSx, a certain percentage λ of piers should reach a local damage index of DSx (or higher); both options were explored, i.e. basing λ on either the number or the area of the piers. A number of possible options were also explored for λ values, i.e. a conservative value λ=0.1, a value λ=0.2 that corresponds to the usual definition of structural failure in a code context, when a strength drop of about 20% takes place, and an upper bound value λ=0.4, which in the case of DS4 corresponds to the global criterion κG=0.6 adopted by the PERPETUATE team (see Table 3).
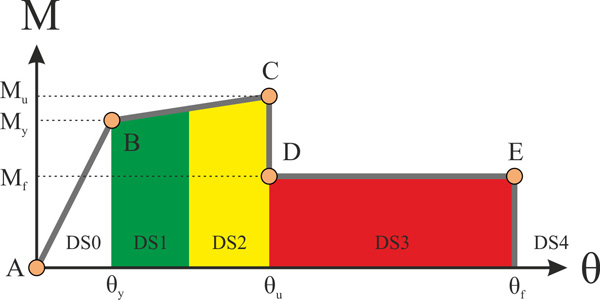 |
Fig. (4). Definition of damage states. |
In addition to the above, the following supplementary criteria were implemented to derive a smooth and reasonable description of the damage evolution:
- In the case that a global damage index is skipped during the transition from one intensity level to the next (e.g. when a PGA transition from 0.5 to 0.6 yields a damage index transition from DS1 to DS3), then the intermediate PGA values corresponding to the skipped damage levels (i.e. DS2) are derived by linear interpolation.
- In the analyses reported in section 3, it was observed that at relatively high excitation levels (above around 0.7 g), some dynamic analyses could not converge for the entire duration of the record. However, in those cases, the lower bound global damage index had already reached the collapse point (DS4) and hence derivation of the corresponding fragility curves was still feasible.
A further criterion, not investigated herein due to absence of sufficient data, but applied in previous works by the senior author and his co-workers [24] in the case of reinforced concrete buildings, is based on the economic damage index, defined [25] as the ratio of the required cost of repair to the pertinent cost of replacement (reconstruction), i.e. the cost corresponding to demolition of the damaged structure and construction of a new ‘identical’ one. This is a particularly meaningful approach in the case of DS1 and DS2, but has difficulties in capturing DS3 and, in particular, DS4; hence, additional criteria similar to the global one proposed previously were used for these damage states in [24].
2.3. Derivation of Fragility Curves
The final step in the proposed procedure is to derive the median threshold values in terms of peak ground acceleration, corresponding to each of the four different damage levels (DS1 to DS4). For each building analysed (in the case study of §3 a URM building is analysed in its pristine, partially and fully strengthened conditions) and each direction (X and Y), the acceleration value corresponding to the first attainment of each damage level is calculated. Since a suite of acceleration records are used, the mean response is taken into account.
In line with most seismic fragility studies, a lognormal distribution was adopted for the acceleration-based fragility curves calculated for each damage state from the relationship:
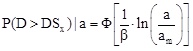 |
(2) |
where P(D>DSx)| is the cumulative probability for damage to reach index DSx for a PGA equal to (a), am is the threshold acceleration of damage state DSx, Φ is the standard normal cumulative distribution function, and β is the standard deviation of the natural logarithm of PGA for damage state DSx. It was beyond the scope of the present study to derive specific values for β based on Monte-Carlo analysis, hence β was taken equal to 0.7 based on the literature [24].
3. Case Studies
The methodology described in §2 was implemented to the fragility analysis of an actual URM building, which is a typical school in Cyprus, wherein a major assessment and retrofit programme for school buildings has been recently completed. 68% of school buildings in Cyprus are made of reinforced concrete, 22% have a dual system consisting of reinforced concrete and masonry, and 10% are made of unreinforced masonry; the majority of the latter are single-storey with load-bearing stone walls and timber pitched roof [26].
3.1. Description of the Building Studied and the Strengthening Schemes
The selected URM building is a single-storey elementary school building located in Limassol, Cyprus; its plan dimensions are 34.75×22.10 m and total height is 7.30 m; it consists of load-bearing limestone masonry with the addition of a timber roof (Fig. 5). No material test data were available for the building, hence strength of masonry units was assessed from tests on limestone units made in other parts of Cyprus and mortar strength was assumed to be 2 MPa; the resulting strength for masonry varied from 4.3 to 8.6 MPa, with a mean value of 6.3 MPa; corresponding elasticity moduli varied from 2.85 to 5.71 GPa (mean value 4.2 MPa).
The building was analysed in its initial (pristine) condition, as well as after applying two alternative strengthening schemes (one of which was actually materialised in this building). The strengthened building was also instrumented and its natural periods identified. As reported in detail in [26], the first two periods of the building were found to be 0.26s and 0.23s, i.e. very close to each other; they were also very close to those predicted by an elastic analysis assuming firm ground conditions.
With respect to the pristine structure, two alternative strengthening schemes are modelled herein:
- addition of a reinforced concrete band (‘chainage’) connecting the perimeter spandrels (this prevents splitting at the corners of the building and provides a small degree of diaphragm action); this was the scheme actually applied to this school in the framework of the strengthening programme
- providing a rigid diaphragm without noticeably affecting the mass of the building (in practice this can be achieved through a steel truss at roof level).
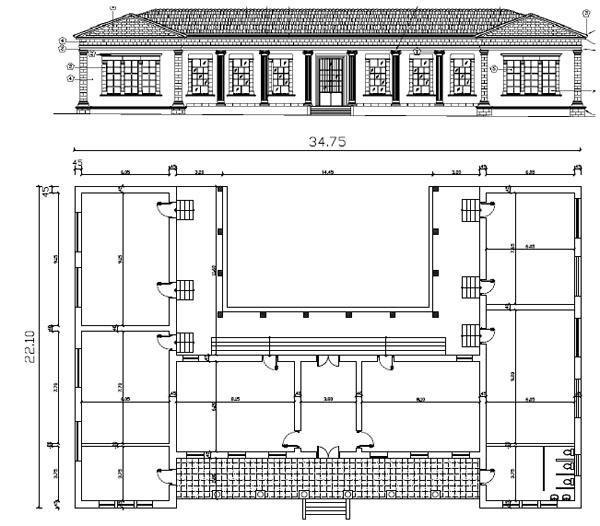 |
Fig. (5). URM building analysed: Front view (top) and plan view (bottom). |
3.2. Modelling of the Building
A preliminary elastic finite element analysis was initially performed, using two modelling approaches, shell elements or equivalent frame elements (Fig. 6). Given the aforementioned uncertainty in masonry strength and also in the ground conditions (both type B and D according to Eurocode 8 were assumed in the analyses) different analyses were run with different material and soil properties [26]. The building strengthened with the chainage was modelled by adding additional reinforced concrete elements (with cross-section 0.45×0.2 m) at the top of the perimeter, which were connected to the adjacent spandrels through rigid arms. The strengthening scheme with the addition of the top diaphragm was simply modelled through the usual diaphragm constraint [17].
It was found that, in the absence of a rigid diaphragm, the modal response is strongly localised Fig. (7) and that the long masonry panels on the perimeter of the building are ineffective in resisting seismic actions transverse to their plane; this is true not only in the initial building but also in the one strengthened with a chainage. The localised nature of the modes is evident from the fact that the fundamental mode has a mass participation ratio of only 5.0%, whereas the mode with the largest participation (16.3%) has a period of 0.08s (about a third that of the first mode), with several modes having participation ratios between 5% and 15%. Regarding the modelling approach, it was confirmed by comparing results from the more and less refined models, that the simpler equivalent frame model showed a modal response similar to that of its more elaborate shell-based counterpart, which renders the former a reliable, as well as practical, choice for performing the set of nonlinear analyses required for the derivation of fragility curves (see discussion on the need for using dynamic in lieu of pushover analysis in §2.1).
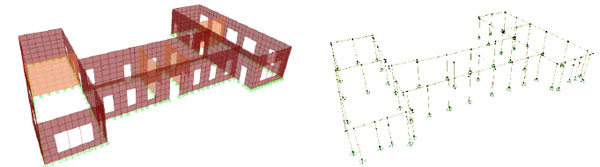 |
Fig. (6). Finite element modelling of the building: shell elements (left) vs. equivalent frame (right). |
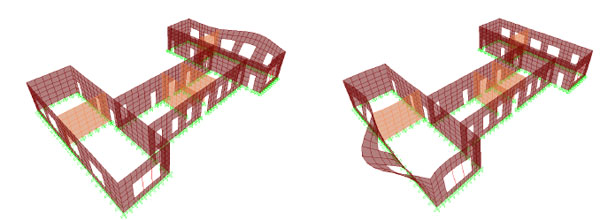 |
Fig. (7). 1st and 2nd mode shapes for the URM building with periods 0.26s and 0.23s respectively. |
Inelastic analysis was carried out using the equivalent frame model (Fig. 6-right), the mean properties of materials and assuming Ground B conditions. The nonlinear model properties were embedded in the form of (potential) plastic hinges on each individual frame (4 hinges for each pier, top/bottom for both directions and 2 hinges for each spandrel, acting in their strong direction). The backbone moment-rotation curves for pier and spandrel hinges were calculated using the methodology described in §2.1. This modelling approach resulted in a total of 180 pier and 66 spandrel hinges. For the hysteretic behaviour of the hinges, a simple kinematic representation was selected (Fig. 3).
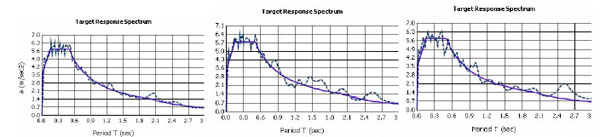 |
Fig. (8). Elastic response spectra of artificial accelerograms, compliant to EN1998 soil type B. |
Loading was applied to the model in two stages: the first step includes gravity loads (self-weight including the timber roof, and 50% of the live loading) and the second the base horizontal acceleration history. Three artificial accelerograms, compatible with the Eurocode 8 [9] spectrum for Ground B were derived (Fig. 8), using in-house developed software [27]. For implementing the incremental dynamic analysis scheme, each record was scaled to 15 different PGA levels, from 0.01g to 1.20g. This set of analyses was repeated for both excitation directions, separately, and for all three different models (pristine structure, partially and fully strengthened structures). To fully automate the incremental dynamic analysis scheme, a custom ad-hoc computer program was implemented using the API interface of the employed finite element software [17]. Mass and stiffness proportional Rayleigh damping (ξ=5%) based on the first two modes was used in the response-history analysis (based on the ΗΤ integration scheme with a = -1/24).
A total of 234 response-history analyses were run. The time for each analysis varied from 15 min to about 12 h, depending on the level of inelasticity induced in the model; this is a good indication of the effort required for this type of analysis, which would have been substantially higher had a more refined (continuum) model been adopted.
3.3. Results of Nonlinear Analysis
Fig. (9) shows typical hysteresis loops recorded at different earthquake intensities; the responses shown in the figure correspond to damage states 1 and 2, whereas an example of DS4 was shown in Fig. (3). It is perhaps worth noting that very few software packages have hysteresis models with strength degradation, which is an essential feature in properly defining damage states, as discussed in §2.2. It should also be noted that these elastoplastic loops overestimate the energy dissipation capacity of URM members. Overall, it was noted that the structure suffers lower damage across its transverse (Y) direction (due to the presence of long masonry panels).
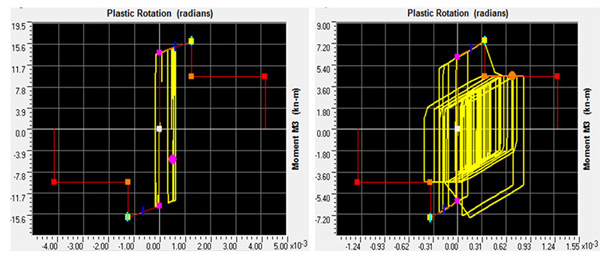 |
Fig. (9). Typical moment vs. plastic rotation response histories for DS1 (left), DS2 damage levels. |
Regarding the damage criteria described in §2.2, the analyses have shown that the ‘upper bound’ condition of 20% pier failures (λ=0.2) is not always reached, even when high accelerations are applied (this is even more the case with the 40% failure criterion). This is due to the fact that substantial damage is localized in specific regions, leaving the rest of the elements nearly intact. In Fig. (10), an indicative damage sequence during inelastic dynamic analysis for the unstrengthened building model is depicted (PGA = 0.6 g). It is clearly seen that the plastic hinges reaching collapse (DS4; red dots) are localized in the front corner piers of the structure.
Table 3 summarises the damage thresholds (in terms of the intensity parameter PGA) for the various DSs estimated by processing the results from response-history analysis of the building (prior to strengthening) subjected to the selected suite of records; the following definitions apply: ‘lower’ means that at least one pier has reached the DS in question; ‘middle’ means that 10% of the piers reach the DS, while ‘high’ means that 20% of the piers reach the DS (the table does not include values for the 40% criterion, for the reasons explained in the previous paragraph). The data in the table confirm the low variability of the response to the input motion characteristics, which points to the convenience of using artificial records whenever no full analysis of uncertainty is deemed essential. It also makes clear the paramount importance of selecting a proper criterion for global DS definition; if the over-conservative criterion of a single pier reaching the DS is adopted, ‘collapse’ (DS4) is reached at PGAs as low as 0.17g, whereas if the more ‘daring’ criterion of 20% failure is invoked, the same DS is only reached when PGA exceeds 1g!
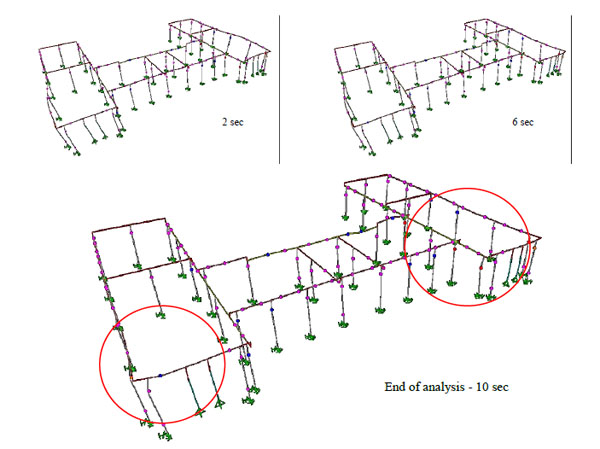 |
Fig. (10). Damage sequence (plastic hinge formation), showing that damage localises at the building corners. |
PGA threshold values (g) for various damage states – pristine structure (X-direction).
| Record | DS1 | DS2 | DS3 | DS4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lower | middle | high | lower | middle | high | lower | middle | high | lower | middle | high | |
| 1 | 0.05 | 0.05 | 0.10 | 0.067 | 0.25 | 0.50 | 0.083 | 0.40 | 0.625 | 0.10 | 0.70 | 0.75 |
| 2 | 0.05 | 0.05 | 0.10 | 0.075 | 0.30 | 0.50 | 0.10 | 0.40 | 0.667 | 0.20 | 0.80 | 1.33 |
| 3 | 0.05 | 0.05 | 0.10 | 0.075 | 0.25 | 0.40 | 0.10 | 0.35 | 0.70 | 0.20 | 0.70 | 1.20 |
| mean | 0.050 | 0.050 | 0.100 | 0.072 | 0.267 | 0.467 | 0.094 | 0.383 | 0.664 | 0.167 | 0.733 | 1.094 |
Results very similar to those in Table 3 are found in the case of the structure strengthened with a chainage; for instance, the DS4 threshold varies from 0.17 to 1.19g, i.e. marginally higher values than those for the unstrengthened building. This should not be interpreted only as an indication of the inefficiency of this technique, but also as a result of the limitation of the nonlinear model used (and most of the URM models found in the literature) that does not account for failure mechanisms such as splitting at the intersection of orthogonal walls, particularly at the corners of the building, which are sometimes observed in older URM buildings. On the contrary, noticeably higher thresholds (i.e. improved performance) are found in the building where a roof diaphragm has been added. For instance, the DS4 threshold varies from 0.50 to 0.93g; the lower value is 3 times that for the unstrengthened building, while the upper value is slightly less, which is not surprising if one notes that the diaphragm leads to a more uniform distribution of damage over the structure (hence more piers fail at a certain level of ground motion). These remarks clearly reveal the sensitivity of the seismic assessment of URM structures to the adopted global damage criteria.
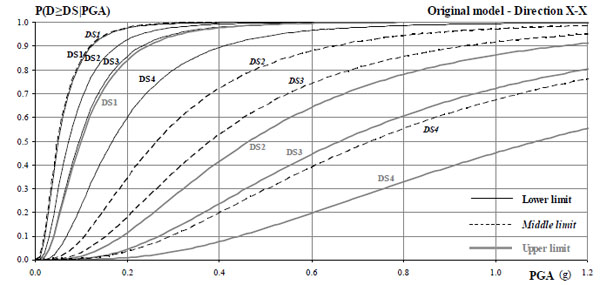 |
Fig. (11). Fragility curves for the pristine building model. |
Finally, regarding the effect of the way the failure rate (λ) is defined, Table 4 shows the (cumulative) percentage of piers exceeding each DS when this is calculated based either on the number of piers or on their area, for different levels of earthquake intensity. It is clear from the table that although the general trends are similar, the area criterion, which in principle makes more sense than the pier count, leads to a less conservative definition of damage states (e.g. for a PGA of 0.7g only 5% of the pier areas reaches DS4) and might not be appropriate for structures with localised modes like the one studied herein. However, the pier count criterion should also be used with caution in the case that several small piers are present in a building, unless their stability is essential to the life safety requirement.
Percentage (%) of piers exceeding each DS, based on member count and on member area.
| DS | a = 0.1g | a = 0.3g | a = 0.5g | a = 0.7g | ||||
|---|---|---|---|---|---|---|---|---|
| Count | Area | Count | Area | Count | Area | Count | Area | |
| 1 | 44.4 | 28.2 | 77.78 | 71.02 | 95.56 | 92.95 | 100.00 | 100.00 |
| 2 | 4.4 | 2.8 | 11.11 | 5.25 | 22.22 | 12.30 | 44.44 | 24.37 |
| 3 | 4.4 | 2.8 | 6.67 | 3.31 | 11.11 | 5.25 | 17.78 | 9.96 |
| 4 | 4.4 | 2.8 | 2.22 | 1.62 | 4.44 | 2.21 | 11.11 | 5.25 |
3.4. Derivation of Fragility Curves
Based on the median values and Eq. 2, fragility curves for the four damage levels (DS1-DS4) were drawn for all cases studied; the sets for the pristine (original) and the rigid diaphragm building models are depicted in Figs. (11, 12) (limits refer to the system in series criterion and the two global criteria, λ=0.1 and λ=0.2, ‘lower’, ‘middle’ and ‘upper’, respectively). The curve set for the case of the reinforced concrete band is very similar to that shown in Fig. (11) for the original building.
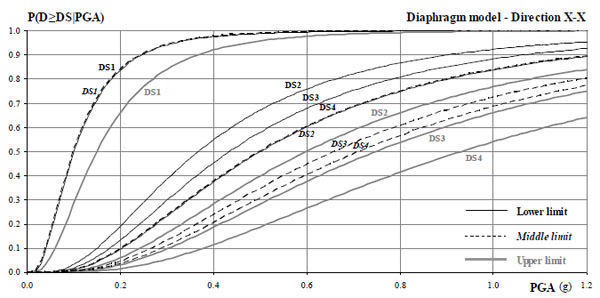 |
Fig. (12). Fragility curves for the fully strengthened building model (rigid diaphragm). |
The key observation from studying the derived fragility curves is the significant uncertainty emanating from the present damage index definitions. More specifically, the lower limit (series system) seems overly conservative, whereas the upper limit of 20% leads to damage thresholds associated with very high (and arguably unrealistic) levels of seismic excitation; the 40% limit (not shown in the figures) leads to unrealistic values and in essence cannot be applied to buildings like the one studied here, wherein damage is not evenly distributed over all structural elements (as in reinforced concrete structures with regular configuration) but rather localizes in certain regions. It is noted that most of the previous similar studies [24] are focused on planar (2D) models, where the uncertainties in the definition of damage levels are fewer compared to the present three-dimensional analysis (i.e. 2D models result in a few translational modes dominating the response, they ignore out-of plane failure, and so on). Overall, the curves resulting from the intermediate criterion (failure of 10% of piers) seem to be the most reasonable ones and formed the basis of a subsequent feasibility analysis.
CONCLUSION AND RECOMMENDATIONS
A number of problems associated with the application of state of the art methods for seismic fragility assessment to URM buildings were identified and a methodology for deriving seismic fragility curves for these buildings using nonlinear response-history analysis has been put forward. This methodology is intended to be applied to practically all types of URM buildings, including (and in particular) those that have no rigid floors or roofs. Seen in a broader context, not all types of common buildings can be treated in a uniform way and proper decisions have to be made to not only select the most suitable methods but also to make them yield compatible results for the various types of buildings forming part of the existing building stock. In the case of reinforced concrete buildings the state of the art is quite advanced and international guidelines like Eurocode 8 - Part 3 [9] can be adopted as a basis for defining damage states that are necessary for fragility assessment. This is not possible in the case of masonry buildings wherein a combination of relationships from the literature with values provided in the pertinent American standard [8] had to be duly tailored in the procedure proposed herein. Even the selection of inelastic analysis method (necessary for deriving fragility curves) is not equally easy in each case. In concrete buildings pushover analysis is in general feasible, noting that in the case of structures with several important modes it has to be applied in its most advanced (and computationally demanding) form of multimodal pushover. For masonry buildings without rigid diaphragms (like the school building studied herein, which is by no means an exceptional case) several local modes are identified and not only application of standard pushover methods is not possible, but even multimodal pushover is practically not feasible. Incremental dynamic analysis is proposed herein for fragility analysis; this is a powerful method, with a broad range of applicability, but is certainly not an easy to apply procedure. In this respect, the importance of availability of proper analysis tools cannot be overemphasised.
The case study presented here has clearly demonstrated the sensitivity of the seismic assessment of URM structures to the adopted global damage criteria. Whereas local damage to piers and spandrels can be predicted in a reasonable way in terms of inelastic deformation (with values based on existing experimental evidence), assigning the entire building to a certain damage state is much more an issue of engineering judgement than of accurate analysis. For the specific building studied and arguably for most types of URM buildings without rigid diaphragms (floors or roof), around 10% of pier failures (at the critical storey, typically the ground one) seems to be a reasonable failure criterion (DS4) whereas the value of 40% proposed in recent studies seems to lead to unreasonable fragility curves (while it has been shown to work in other types of URM buildings [6]). As a general recommendation, the qualified engineer carrying out the fragility-based loss assessment should carefully examine the specific building (or class of buildings) at hand, assess ad hoc the implications of local failures (in particular with respect to life safety) and also carry out two or more sensitivity analyses invoking different global failure criteria. It is recognised that whereas this cumbersome procedure is feasible in the case of building specific assessments, it cannot be applied to large-scale loss studies, wherein reasonably conservative damage thresholds should be adopted.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
AKCNOWLEDGEMENTS
Part of the work reported herein was carried out in the framework of the project ΑΕΙΦΟΡΙΑ/ΑΣΤΙ/0609(ΒΙΕ)/06 funded under DESMI 2009-10 of the Research Promotion Foundation of Cyprus and by the Cyprus Government and the European Regional Development Fund.








